线性代数张宇9讲 第八讲 相似矩阵与相似对角化
目录
- 例题八
- 例8.14 设 A \bm{A} A为 3 3 3阶矩阵, α 1 , α 2 , α 3 \bm{\alpha}_1,\bm{\alpha}_2,\bm{\alpha}_3 α1,α2,α3是线性无关的 3 3 3维列向量,且满足 A α 1 = α 1 + α 2 + α 3 , A α 2 = 2 α 2 + α 3 , A α 3 = 2 α 2 + 3 α 3 . \bm{A\alpha}_1=\bm{\alpha}_1+\bm{\alpha}_2+\bm{\alpha}_3,\\\bm{A\alpha}_2=2\bm{\alpha}_2+\bm{\alpha}_3,\\\bm{A\alpha}_3=2\bm{\alpha}_2+3\bm{\alpha}_3. Aα1=α1+α2+α3,Aα2=2α2+α3,Aα3=2α2+3α3.
- (1)求矩阵 B \bm{B} B,使得 A [ α 1 , α 2 , α 3 ] = [ α 1 , α 2 , α 3 ] B \bm{A}[\bm{\alpha}_1,\bm{\alpha}_2,\bm{\alpha}_3]=[\bm{\alpha}_1,\bm{\alpha}_2,\bm{\alpha}_3]\bm{B} A[α1,α2,α3]=[α1,α2,α3]B;
- (2)求矩阵 A \bm{A} A的特征值;
- (3)求可逆矩阵 P \bm{P} P,使得 P − 1 A P \bm{P}^{-1}\bm{AP} P−1AP为对角矩阵。
- 例8.15 证明:实对称矩阵 A \bm{A} A对应于不同特征值的特征向量是正交的。
- 例8.28 设 A = [ 1 − 2 0 0 − 1 0 0 0 0 0 2 1 0 0 0 2 ] \bm{A}=\begin{bmatrix}1&-2&0&0\\-1&0&0&0\\0&0&2&1\\0&0&0&2\end{bmatrix} A=⎣⎢⎢⎡1−100−200000200012⎦⎥⎥⎤,求 A n \bm{A}^n An。
- 例8.31 设 A \bm{A} A是 n n n阶正定矩阵,证明:存在 n n n阶正定矩阵 B \bm{B} B,使得 A = B 2 \bm{A}=\bm{B}^2 A=B2。
- 新版例题八
- 例8.4
- 例8.8
- 例8.14
- 例8.15
- 新版习题八
- 8.2
- 8.6
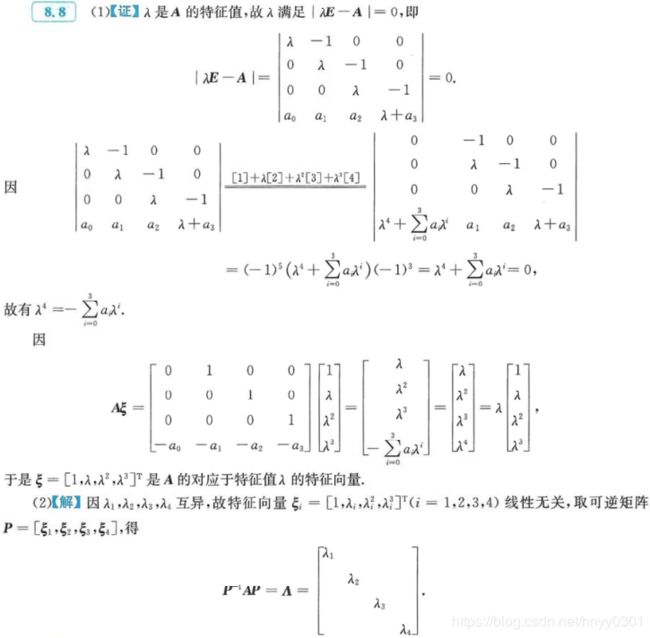
- 8.8
- 8.13
- 8.14
- 写在最后
例题八
例8.14 设 A \bm{A} A为 3 3 3阶矩阵, α 1 , α 2 , α 3 \bm{\alpha}_1,\bm{\alpha}_2,\bm{\alpha}_3 α1,α2,α3是线性无关的 3 3 3维列向量,且满足 A α 1 = α 1 + α 2 + α 3 , A α 2 = 2 α 2 + α 3 , A α 3 = 2 α 2 + 3 α 3 . \bm{A\alpha}_1=\bm{\alpha}_1+\bm{\alpha}_2+\bm{\alpha}_3,\\\bm{A\alpha}_2=2\bm{\alpha}_2+\bm{\alpha}_3,\\\bm{A\alpha}_3=2\bm{\alpha}_2+3\bm{\alpha}_3. Aα1=α1+α2+α3,Aα2=2α2+α3,Aα3=2α2+3α3.
(1)求矩阵 B \bm{B} B,使得 A [ α 1 , α 2 , α 3 ] = [ α 1 , α 2 , α 3 ] B \bm{A}[\bm{\alpha}_1,\bm{\alpha}_2,\bm{\alpha}_3]=[\bm{\alpha}_1,\bm{\alpha}_2,\bm{\alpha}_3]\bm{B} A[α1,α2,α3]=[α1,α2,α3]B;
解 将题设条件合并成矩阵形式有
A [ α 1 , α 2 , α 3 ] = [ A α 1 , A α 2 , A α 3 ] = [ α 1 + α 2 + α 3 , 2 α 2 + α 3 , 2 α 2 + 3 α 3 ] = [ α 1 , α 2 , α 3 ] [ 1 0 0 1 2 2 1 1 3 ] , \begin{aligned} \bm{A}[\bm{\alpha}_1,\bm{\alpha}_2,\bm{\alpha}_3]&=[\bm{A\alpha}_1,\bm{A\alpha}_2,\bm{A\alpha}_3]=[\bm{\alpha}_1+\bm{\alpha}_2+\bm{\alpha}_3,2\bm{\alpha}_2+\bm{\alpha}_3,2\bm{\alpha}_2+3\bm{\alpha}_3]\\ &=[\bm{\alpha}_1,\bm{\alpha}_2,\bm{\alpha}_3]\begin{bmatrix}1&0&0\\1&2&2\\1&1&3\end{bmatrix}, \end{aligned} A[α1,α2,α3]=[Aα1,Aα2,Aα3]=[α1+α2+α3,2α2+α3,2α2+3α3]=[α1,α2,α3]⎣⎡111021023⎦⎤,
故 B = [ 1 0 0 1 2 2 1 1 3 ] \bm{B}=\begin{bmatrix}1&0&0\\1&2&2\\1&1&3\end{bmatrix} B=⎣⎡111021023⎦⎤。
(2)求矩阵 A \bm{A} A的特征值;
解 因 α 1 , α 2 , α 3 \bm{\alpha}_1,\bm{\alpha}_2,\bm{\alpha}_3 α1,α2,α3线性无关,故 C = [ α 1 , α 2 , α 3 ] \bm{C}=[\bm{\alpha}_1,\bm{\alpha}_2,\bm{\alpha}_3] C=[α1,α2,α3]是可逆矩阵,且有 C − 1 A C = B \bm{C}^{-1}\bm{AC}=\bm{B} C−1AC=B,即 A \bm{A} A和 B \bm{B} B相似,相似矩阵有相同的特征值。因
∣ λ E − B ∣ = ∣ λ − 1 0 0 − 1 λ − 2 − 2 − 1 − 1 λ − 3 ∣ = ( λ − 1 ) ( λ 2 − 5 λ + 4 ) = ( λ − 1 ) 2 ( λ − 4 ) = 0 , |\lambda\bm{E}-\bm{B}|=\begin{vmatrix}\lambda-1&0&0\\-1&\lambda-2&-2\\-1&-1&\lambda-3\end{vmatrix}=(\lambda-1)(\lambda^2-5\lambda+4)=(\lambda-1)^2(\lambda-4)=0, ∣λE−B∣=∣∣∣∣∣∣λ−1−1−10λ−2−10−2λ−3∣∣∣∣∣∣=(λ−1)(λ2−5λ+4)=(λ−1)2(λ−4)=0,
故 B \bm{B} B的特征值为 1 , 1 , 4 1,1,4 1,1,4,所以 A \bm{A} A的特征值也为 1 , 1 , 4 1,1,4 1,1,4。
(3)求可逆矩阵 P \bm{P} P,使得 P − 1 A P \bm{P}^{-1}\bm{AP} P−1AP为对角矩阵。
解 对于矩阵 B \bm{B} B,当 λ 1 = λ 2 = 1 \lambda_1=\lambda_2=1 λ1=λ2=1时,由 ( E − B ) x = 0 (\bm{E}-\bm{B})\bm{x}=\bm{0} (E−B)x=0,即
[ 0 0 0 − 1 − 1 − 2 − 1 − 1 − 2 ] [ x 1 x 2 x 3 ] = [ 0 0 0 ] , \begin{bmatrix}0&0&0\\-1&-1&-2\\-1&-1&-2\end{bmatrix}\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}=\begin{bmatrix}0\\0\\0\end{bmatrix}, ⎣⎡0−1−10−1−10−2−2⎦⎤⎣⎡x1x2x3⎦⎤=⎣⎡000⎦⎤,
得基础解系 ξ 1 = [ 1 , − 1 , 0 ] T , ξ 2 = [ − 2 , 0 , 1 ] T \bm{\xi}_1=[1,-1,0]^\mathrm{T},\bm{\xi}_2=[-2,0,1]^\mathrm{T} ξ1=[1,−1,0]T,ξ2=[−2,0,1]T;
当 λ 3 = 4 \lambda_3=4 λ3=4时,由 ( E − B ) x = 0 (\bm{E}-\bm{B})\bm{x}=\bm{0} (E−B)x=0,即
[ 3 0 0 − 1 2 − 2 − 1 − 1 1 ] [ x 1 x 2 x 3 ] = [ 0 0 0 ] , \begin{bmatrix}3&0&0\\-1&2&-2\\-1&-1&1\end{bmatrix}\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}=\begin{bmatrix}0\\0\\0\end{bmatrix}, ⎣⎡3−1−102−10−21⎦⎤⎣⎡x1x2x3⎦⎤=⎣⎡000⎦⎤,
得基础解系 ξ 3 = [ 0 , 1 , 1 ] T \bm{\xi}_3=[0,1,1]^\mathrm{T} ξ3=[0,1,1]T。
令 Q = [ ξ 1 , ξ 2 , ξ 3 ] = [ 1 − 2 0 − 1 0 1 0 1 1 ] \bm{Q}=[\bm{\xi}_1,\bm{\xi}_2,\bm{\xi}_3]=\begin{bmatrix}1&-2&0\\-1&0&1\\0&1&1\end{bmatrix} Q=[ξ1,ξ2,ξ3]=⎣⎡1−10−201011⎦⎤,有 Q − 1 B Q = Λ = [ 1 0 0 0 1 0 0 0 4 ] \bm{Q}^{-1}\bm{BQ}=\bm{\varLambda}=\begin{bmatrix}1&0&0\\0&1&0\\0&0&4\end{bmatrix} Q−1BQ=Λ=⎣⎡100010004⎦⎤,故有
Q − 1 B Q = Q − 1 C − 1 A C Q = Λ = [ 1 0 0 0 1 0 0 0 4 ] . \bm{Q}^{-1}\bm{BQ}=\bm{Q}^{-1}\bm{C}^{-1}\bm{ACQ}=\bm{\varLambda}=\begin{bmatrix}1&0&0\\0&1&0\\0&0&4\end{bmatrix}. Q−1BQ=Q−1C−1ACQ=Λ=⎣⎡100010004⎦⎤.
取 P = C Q = [ α 1 , α 2 , α 3 ] [ 1 − 2 0 − 1 0 1 0 1 1 ] = [ α 1 − α 2 , − 2 α 1 + α 3 , α 2 + α 3 ] \bm{P}=\bm{CQ}=[\bm{\alpha}_1,\bm{\alpha}_2,\bm{\alpha}_3]\begin{bmatrix}1&-2&0\\-1&0&1\\0&1&1\end{bmatrix}=[\bm{\alpha}_1-\bm{\alpha}_2,-2\bm{\alpha}_1+\bm{\alpha}_3,\bm{\alpha}_2+\bm{\alpha}_3] P=CQ=[α1,α2,α3]⎣⎡1−10−201011⎦⎤=[α1−α2,−2α1+α3,α2+α3],则有
P − 1 A P = [ 1 0 0 0 1 0 0 0 4 ] . \bm{P}^{-1}\bm{AP}=\begin{bmatrix}1&0&0\\0&1&0\\0&0&4\end{bmatrix}. P−1AP=⎣⎡100010004⎦⎤.
(这道题主要利用了构造矩阵求解)
例8.15 证明:实对称矩阵 A \bm{A} A对应于不同特征值的特征向量是正交的。
证 设 A x i = λ i x i ( x i ≠ 0 , i = 1 , 2 ) , λ 1 ≠ λ 2 , A T = A \bm{Ax}_i=\lambda_i\bm{x}_i(\bm{x}_i\ne\bm{0},i=1,2),\lambda_1\ne\lambda_2,\bm{A}^\mathrm{T}=\bm{A} Axi=λixi(xi=0,i=1,2),λ1=λ2,AT=A,则
λ 1 x 2 T x 1 = x 2 T A x 1 = x 2 T A T x 1 = ( A x 2 ) T x 1 = ( λ 2 x 2 ) T x 1 = λ 2 x 2 T x 1 . \begin{aligned} \lambda_1\bm{x}_2^\mathrm{T}\bm{x}_1&=\bm{x}_2^\mathrm{T}\bm{Ax}_1=\bm{x}_2^\mathrm{T}\bm{A}^\mathrm{T}\bm{x}_1=(\bm{Ax}_2)^\mathrm{T}\bm{x}_1\\ &=(\lambda_2\bm{x}_2)^\mathrm{T}\bm{x}_1=\lambda_2\bm{x}_2^\mathrm{T}\bm{x}_1. \end{aligned} λ1x2Tx1=x2TAx1=x2TATx1=(Ax2)Tx1=(λ2x2)Tx1=λ2x2Tx1.
由于 λ 1 ≠ λ 2 \lambda_1\ne\lambda_2 λ1=λ2,所以 x 2 T x 1 ≠ 0 \bm{x}_2^\mathrm{T}\bm{x}_1\ne0 x2Tx1=0,即 ( x 1 , x 2 ) ≠ 0 (\bm{x}_1,\bm{x}_2)\ne0 (x1,x2)=0,故当 x 1 , x 2 \bm{x}_1,\bm{x}_2 x1,x2为实对称矩阵 A \bm{A} A对应于不同特征值的特征向量时, x 1 \bm{x}_1 x1与 x 2 \bm{x}_2 x2正交。(这道题主要利用了转置矩阵的性质求解)
例8.28 设 A = [ 1 − 2 0 0 − 1 0 0 0 0 0 2 1 0 0 0 2 ] \bm{A}=\begin{bmatrix}1&-2&0&0\\-1&0&0&0\\0&0&2&1\\0&0&0&2\end{bmatrix} A=⎣⎢⎢⎡1−100−200000200012⎦⎥⎥⎤,求 A n \bm{A}^n An。
解 A \bm{A} A是分块对角矩阵,记 A = [ B O O C ] \bm{A}=\begin{bmatrix}\bm{B}&\bm{O}\\\bm{O}&\bm{C}\end{bmatrix} A=[BOOC],其中 B = [ 1 − 2 − 1 0 ] , C = [ 2 1 0 2 ] \bm{B}=\begin{bmatrix}1&-2\\-1&0\end{bmatrix},\bm{C}=\begin{bmatrix}2&1\\0&2\end{bmatrix} B=[1−1−20],C=[2012],则
A n = [ B O O C ] n = [ B n O O C n ] . \bm{A}^n=\begin{bmatrix}\bm{B}&\bm{O}\\\bm{O}&\bm{C}\end{bmatrix}^n=\begin{bmatrix}\bm{B}^n&\bm{O}\\\bm{O}&\bm{C}^n\end{bmatrix}. An=[BOOC]n=[BnOOCn].
对于 B = [ 1 − 2 − 1 0 ] , ∣ λ E − B ∣ = [ λ − 1 2 1 λ ] = ( λ + 1 ) ( λ − 2 ) = 0 \bm{B}=\begin{bmatrix}1&-2\\-1&0\end{bmatrix},|\lambda\bm{E}-\bm{B}|=\begin{bmatrix}\lambda-1&2\\1&\lambda\end{bmatrix}=(\lambda+1)(\lambda-2)=0 B=[1−1−20],∣λE−B∣=[λ−112λ]=(λ+1)(λ−2)=0,对应的特征值为 λ 1 = − 1 , λ 2 = 2 \lambda_1=-1,\lambda_2=2 λ1=−1,λ2=2。
当 λ 1 = − 1 \lambda_1=-1 λ1=−1时,由 ( λ 1 E − B ) x = 0 (\lambda_1\bm{E}-\bm{B})\bm{x}=\bm{0} (λ1E−B)x=0,得 ξ 1 = [ 1 , 1 ] T \bm{\xi}_1=[1,1]^\mathrm{T} ξ1=[1,1]T;
当 λ 2 = 2 \lambda_2=2 λ2=2时,由 ( λ 2 E − B ) x = 0 (\lambda_2\bm{E}-\bm{B})\bm{x}=\bm{0} (λ2E−B)x=0,得 ξ 2 = [ − 2 , 1 ] T \bm{\xi}_2=[-2,1]^\mathrm{T} ξ2=[−2,1]T。
于是有
P − 1 B P = [ − 1 0 0 2 ] , 其中 P = [ 1 − 2 1 1 ] , P − 1 = 1 3 [ 1 2 − 1 1 ] , \bm{P}^{-1}\bm{BP}=\begin{bmatrix}-1&0\\0&2\end{bmatrix},\text{其中}\bm{P}=\begin{bmatrix}1&-2\\1&1\end{bmatrix},\bm{P}^{-1}=\cfrac{1}{3}\begin{bmatrix}1&2\\-1&1\end{bmatrix}, P−1BP=[−1002],其中P=[11−21],P−1=31[1−121],
故
B n = ( P [ − 1 0 0 2 ] P − 1 ) n = P [ − 1 0 0 2 ] n P − 1 = 1 3 [ 1 − 2 1 1 ] [ ( − 1 ) n 0 0 2 n ] [ 1 2 − 1 1 ] = 1 3 [ ( − 1 ) n + 2 n + 1 ( − 1 ) n ⋅ 2 − 2 n + 1 ( − 1 ) n − 2 n ( − 1 ) n ⋅ 2 + 2 n ] . \begin{aligned} \bm{B}^n&=\left(\bm{P}\begin{bmatrix}-1&0\\0&2\end{bmatrix}\bm{P}^{-1}\right)^n=\bm{P}\begin{bmatrix}-1&0\\0&2\end{bmatrix}^n\bm{P}^{-1}\\ &=\cfrac{1}{3}\begin{bmatrix}1&-2\\1&1\end{bmatrix}\begin{bmatrix}(-1)^n&0\\0&2^n\end{bmatrix}\begin{bmatrix}1&2\\-1&1\end{bmatrix}\\ &=\cfrac{1}{3}\begin{bmatrix}(-1)^n+2^{n+1}&(-1)^n\cdot2-2^{n+1}\\(-1)^n-2^{n}&(-1)^n\cdot2+2^{n}\end{bmatrix}. \end{aligned} Bn=(P[−1002]P−1)n=P[−1002]nP−1=31[11−21][(−1)n002n][1−121]=31[(−1)n+2n+1(−1)n−2n(−1)n⋅2−2n+1(−1)n⋅2+2n].
对于 C = [ 2 1 0 2 ] \bm{C}=\begin{bmatrix}2&1\\0&2\end{bmatrix} C=[2012],因当 n ⩾ 2 n\geqslant2 n⩾2时, [ 0 1 0 0 ] n = O \begin{bmatrix}0&1\\0&0\end{bmatrix}^n=\bm{O} [0010]n=O,故
C n = ( 2 E + [ 0 1 0 0 ] ) n = 2 n E n + n ⋅ 2 n − 1 E n − 1 [ 0 1 0 0 ] = [ 2 n n ⋅ 2 n − 1 0 2 n ] , \bm{C}^n=\left(2\bm{E}+\begin{bmatrix}0&1\\0&0\end{bmatrix}\right)^n=2^n\bm{E}^n+n\cdot2^{n-1}\bm{E}^{n-1}\begin{bmatrix}0&1\\0&0\end{bmatrix}=\begin{bmatrix}2^n&n\cdot2^{n-1}\\0&2^n\end{bmatrix}, Cn=(2E+[0010])n=2nEn+n⋅2n−1En−1[0010]=[2n0n⋅2n−12n],
因此,
A n = [ B n O O C n ] = [ 1 3 ( − 1 ) n + 1 3 ⋅ 2 n + 1 2 3 ( − 1 ) n − 1 3 ⋅ 2 n + 1 0 0 1 3 ( − 1 ) n − 1 3 ⋅ 2 n 2 3 ( − 1 ) n + 1 3 ⋅ 2 n 0 0 0 0 2 n n ⋅ 2 n − 1 0 0 0 2 n ] . \bm{A}^n=\begin{bmatrix}\bm{B}^n&\bm{O}\\\bm{O}&\bm{C}^n\end{bmatrix}=\begin{bmatrix}\cfrac{1}{3}(-1)^n+\cfrac{1}{3}\cdot2^{n+1}&\cfrac{2}{3}(-1)^n-\cfrac{1}{3}\cdot2^{n+1}&0&0\\\cfrac{1}{3}(-1)^n-\cfrac{1}{3}\cdot2^{n}&\cfrac{2}{3}(-1)^n+\cfrac{1}{3}\cdot2^{n}&0&0\\0&0&2^n&n\cdot2^{n-1}\\0&0&0&2^n\end{bmatrix}. An=[BnOOCn]=⎣⎢⎢⎢⎢⎢⎡31(−1)n+31⋅2n+131(−1)n−31⋅2n0032(−1)n−31⋅2n+132(−1)n+31⋅2n00002n000n⋅2n−12n⎦⎥⎥⎥⎥⎥⎤.
(这道题主要利用了分块矩阵求解)
例8.31 设 A \bm{A} A是 n n n阶正定矩阵,证明:存在 n n n阶正定矩阵 B \bm{B} B,使得 A = B 2 \bm{A}=\bm{B}^2 A=B2。
证 由 A \bm{A} A是正定矩阵,必为实对称矩阵,故存在正交矩阵 Q \bm{Q} Q,使得
Q − 1 A Q = [ λ 1 λ 2 ⋱ λ n ] , \bm{Q}^{-1}\bm{AQ}=\begin{bmatrix}\lambda_1&&&\\&\lambda_2&&\\&&\ddots&\\&&&\lambda_n\end{bmatrix}, Q−1AQ=⎣⎢⎢⎡λ1λ2⋱λn⎦⎥⎥⎤,
且 λ i > 0 ( i = 1 , 2 , ⋯ , n ) \lambda_i>0(i=1,2,\cdots,n) λi>0(i=1,2,⋯,n),从而
A = Q [ λ 1 λ 2 ⋱ λ n ] Q − 1 = Q [ λ 1 λ 2 ⋱ λ n ] [ λ 1 λ 2 ⋱ λ n ] Q − 1 = Q [ λ 1 λ 2 ⋱ λ n ] Q − 1 Q [ λ 1 λ 2 ⋱ λ n ] Q − 1 = B 2 , \begin{aligned} \bm{A}&=\bm{Q}\begin{bmatrix}\lambda_1&&&\\&\lambda_2&&\\&&\ddots&\\&&&\lambda_n\end{bmatrix}\bm{Q}^{-1}\\ &=\bm{Q}\begin{bmatrix}\sqrt{\lambda_1}&&&\\&\sqrt{\lambda_2}&&\\&&\ddots&\\&&&\sqrt{\lambda_n}\end{bmatrix}\begin{bmatrix}\sqrt{\lambda_1}&&&\\&\sqrt{\lambda_2}&&\\&&\ddots&\\&&&\sqrt{\lambda_n}\end{bmatrix}\bm{Q}^{-1}\\ &=\bm{Q}\begin{bmatrix}\sqrt{\lambda_1}&&&\\&\sqrt{\lambda_2}&&\\&&\ddots&\\&&&\sqrt{\lambda_n}\end{bmatrix}\bm{Q}^{-1}\bm{Q}\begin{bmatrix}\sqrt{\lambda_1}&&&\\&\sqrt{\lambda_2}&&\\&&\ddots&\\&&&\sqrt{\lambda_n}\end{bmatrix}\bm{Q}^{-1}\\ &=\bm{B}^2, \end{aligned} A=Q⎣⎢⎢⎡λ1λ2⋱λn⎦⎥⎥⎤Q−1=Q⎣⎢⎢⎡λ1λ2⋱λn⎦⎥⎥⎤⎣⎢⎢⎡λ1λ2⋱λn⎦⎥⎥⎤Q−1=Q⎣⎢⎢⎡λ1λ2⋱λn⎦⎥⎥⎤Q−1Q⎣⎢⎢⎡λ1λ2⋱λn⎦⎥⎥⎤Q−1=B2,
其中
B = Q [ λ 1 λ 2 ⋱ λ n ] Q − 1 , \bm{B}=\bm{Q}\begin{bmatrix}\sqrt{\lambda_1}&&&\\&\sqrt{\lambda_2}&&\\&&\ddots&\\&&&\sqrt{\lambda_n}\end{bmatrix}\bm{Q}^{-1}, B=Q⎣⎢⎢⎡λ1λ2⋱λn⎦⎥⎥⎤Q−1,
则
B ∼ [ λ 1 λ 2 ⋱ λ n ] . \bm{B}\sim\begin{bmatrix}\sqrt{\lambda_1}&&&\\&\sqrt{\lambda_2}&&\\&&\ddots&\\&&&\sqrt{\lambda_n}\end{bmatrix}. B∼⎣⎢⎢⎡λ1λ2⋱λn⎦⎥⎥⎤.
所以矩阵 B \bm{B} B的特征值是 λ 1 , λ 2 , ⋯ , λ n \sqrt{\lambda_1},\sqrt{\lambda_2},\cdots,\sqrt{\lambda_n} λ1,λ2,⋯,λn,且均大于 0 0 0。又易知 B \bm{B} B是实对称矩阵,因此 B \bm{B} B是正定矩阵,且满足 A = B 2 \bm{A}=\bm{B}^2 A=B2。(这道题主要利用了矩阵的初等变换求解)
新版例题八
例8.4
例8.8
例8.14
例8.15
新版习题八
8.2
8.6
8.8
8.13
8.14
写在最后
如果觉得文章不错就点个赞吧。另外,如果有不同的观点,欢迎留言或私信。
欢迎非商业转载,转载请注明出处。