动手学深度学习——卷积神经网络1

白嫖伯禹平台，还是要感谢一下，打波广告。
主要是学习笔记，解决问题的可以忽略本博客，以免浪费时间与精力

卷积神经网络基础

主要介绍卷积神经网络的基础概念，主要是卷积层和池化层，并解释填充、步幅、输入通道和输出通道的含义。

二维互相关运算

官方解释：二维互相关（cross-correlation）运算的输入是一个二维输入数组和一个二维核（kernel）数组，输出也是一个二维数组，其中核数组通常称为卷积核或过滤器（filter）。卷积核的尺寸通常小于输入数组，卷积核在输入数组上滑动，在每个位置上，卷积核与该位置处的输入子数组按元素相乘并求和，得到输出数组中相应位置的元素。图1展示了一个互相关运算的例子，阴影部分分别是输入的第一个计算区域、核数组以及对应的输出。

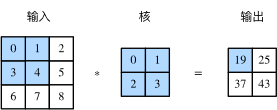
通俗的个人理解就是：卷积核与覆盖的输入数组，进行点乘运算注意不是矩阵运算 ，以上图为例 运算过程就是 00+11+32+43 = 19
Pytorch 中使用 corr2d 函数可以实现二维互相关运算，它接受输入数组X与核数组K，并输出数组Y。

import torch 
import torch.nn as nn

def corr2d(X, K):
	# X代表输入数组，K代表卷积核
	# H/h 行,W/w代表列
    H, W = X.shape
    h, w = K.shape
    Y = torch.zeros(H - h + 1, W - w + 1)
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = (X[i: i + h, j: j + w] * K).sum()
    return Y

构造上图中的输入数组X、核数组K来验证二维互相关运算的输出

X = torch.tensor([[0, 1, 2], [3, 4, 5], [6, 7, 8]])
K = torch.tensor([[0, 1], [2, 3]])
Y = corr2d(X, K)
print(Y)

输出结果tensor([[19., 25.], [37., 43.]])

二维卷积层

二维卷积层将输入和卷积核做互相关运算，并加上一个标量偏置来得到输出。卷积层的模型参数包括卷积核和标量偏置。

class Conv2D(nn.Module):
    def __init__(self, kernel_size):
        super(Conv2D, self).__init__()
        self.weight = nn.Parameter(torch.randn(kernel_size))
        self.bias = nn.Parameter(torch.randn(1))

    def forward(self, x):
        return corr2d(x, self.weight) + self.bias

下面我们看一个例子，我们构造一张 6×8 的图像，中间4列为黑（0），其余为白（1），希望检测到颜色边缘。我们的标签是一个 6×7 的二维数组，第2列是1（从1到0的边缘），第6列是-1（从0到1的边缘）。

X = torch.ones(6, 8)
Y = torch.zeros(6, 7)
X[:, 2: 6] = 0
Y[:, 1] = 1
Y[:, 5] = -1
print(X)
print(Y)

输出结果
tensor([[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.]])
tensor([[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.]])
希望学习希望学习一个 1×2 卷积层，通过卷积层来检测颜色边缘。

conv2d = Conv2D(kernel_size=(1, 2))
step = 30  #周期
lr = 0.01 # 学习率
for i in range(step):
    Y_hat = conv2d(X)
    l = ((Y_hat - Y) ** 2).sum()
    l.backward()
    # 梯度下降
    conv2d.weight.data -= lr * conv2d.weight.grad
    conv2d.bias.data -= lr * conv2d.bias.grad
    
    # 梯度清零
    conv2d.weight.grad.zero_()
    conv2d.bias.grad.zero_()
    if (i + 1) % 5 == 0:
        print('Step %d, loss %.3f' % (i + 1, l.item()))
        
print(conv2d.weight.data)
print(conv2d.bias.data)

运算结果
Step 5, loss 4.569
Step 10, loss 0.949
Step 15, loss 0.228
Step 20, loss 0.060
Step 25, loss 0.016
Step 30, loss 0.004
tensor([[ 1.0161, -1.0177]])
tensor([0.0009])

填充和步幅

介绍卷积层的两个超参数，即填充和步幅，它们可以对给定形状的输入和卷积核改变输出形状。

填充

填充（padding）是指在输入高和宽的两侧填充元素（通常是0元素），图2里我们在原输入高和宽的两侧分别添加了值为0的元素。

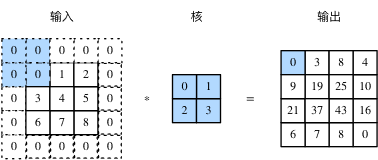
图2 在输入的高和宽两侧分别填充了0元素的二维互相关计算

如果原输入的高和宽是 nh 和 nw ，卷积核的高和宽是 kh 和 kw ，在高的两侧一共填充 ph 行，在宽的两侧一共填充 pw 列，则输出形状为：

(nh+ph−kh+1)×(nw+pw−kw+1)

我们在卷积神经网络中使用奇数高宽的核，比如 3×3 ， 5×5 的卷积核，对于高度（或宽度）为大小为 2k+1 的核，令步幅为1，在高（或宽）两侧选择大小为 k 的填充，便可保持输入与输出尺寸相同。
简而言之填充就是在输入数组周围填充制定元素，例如padding = 1 那么上下左右全都要填充一行0元素

步幅

在互相关运算中，卷积核在输入数组上滑动，每次滑动的行数与列数即是步幅（stride）。此前我们使用的步幅都是1，图3展示了在高上步幅为3、在宽上步幅为2的二维互相关运算。
也是横向每次移动2格，纵向每次移动3格

图3 高和宽上步幅分别为3和2的二维互相关运算

一般来说，当高上步幅为 sh ，宽上步幅为 sw 时，输出形状为：

⌊(nh+ph−kh+sh)/sh⌋×⌊(nw+pw−kw+sw)/sw⌋

如果 ph=kh−1 ， pw=kw−1 ，那么输出形状将简化为 ⌊(nh+sh−1)/sh⌋×⌊(nw+sw−1)/sw⌋ 。更进一步，如果输入的高和宽能分别被高和宽上的步幅整除，那么输出形状将是 (nh/sh)×(nw/sw) 。

当 ph=pw=p 时，我们称填充为 p ；当 sh=sw=s 时，我们称步幅为 s 。

有一个万能公式 （H-F+ 2P）/S +1
H 输入数组尺寸，F卷积核尺寸，P 填充数组，S 移动步长 加1 表示偏置

多输入通道和多输出通道

之前的输入和输出都是二维数组，但真实数据的维度经常更高。例如，彩色图像在高和宽2个维度外还有RGB（红、绿、蓝）3个颜色通道。假设彩色图像的高和宽分别是 h 和 w （像素），那么它可以表示为一个 3×h×w 的多维数组，我们将大小为3的这一维称为通道（channel）维。

多输入通道单输出

卷积层的输入可以包含多个通道，图4展示了一个含2个输入通道的二维互相关计算的例子。

假设输入数据的通道数为 ci ，卷积核形状为 kh×kw ，我们为每个输入通道各分配一个形状为 kh×kw 的核数组，将 ci 个互相关运算的二维输出按通道相加，得到一个二维数组作为输出。我们把 ci 个核数组在通道维上连结，即得到一个形状为 ci×kh×kw 的卷积核。

多输入与多输出通道

卷积层的输出也可以包含多个通道，设卷积核输入通道数和输出通道数分别为 ci 和 co ，高和宽分别为 kh 和 kw 。如果希望得到含多个通道的输出，我们可以为每个输出通道分别创建形状为 ci×kh×kw 的核数组，将它们在输出通道维上连结，卷积核的形状即 co×ci×kh×kw 。

对于输出通道的卷积核，我们提供这样一种理解，一个 ci×kh×kw 的核数组可以提取某种局部特征，但是输入可能具有相当丰富的特征，我们需要有多个这样的 ci×kh×kw 的核数组，不同的核数组提取的是不同的特征。

1X1 卷积层

最后讨论形状为 1×1 的卷积核，我们通常称这样的卷积运算为 1×1 卷积，称包含这种卷积核的卷积层为 1×1 卷积层。图5展示了使用输入通道数为3、输出通道数为2的 1×1 卷积核的互相关计算。

图5 1x1卷积核的互相关计算。输入和输出具有相同的高和宽

1×1 卷积核可在不改变高宽的情况下，调整通道数。 1×1 卷积核不识别高和宽维度上相邻元素构成的模式，其主要计算发生在通道维上。假设我们将通道维当作特征维，将高和宽维度上的元素当成数据样本，那么 1×1 卷积层的作用与全连接层等价。

卷积层与全连接层的对比

二维卷积层经常用于处理图像，与此前的全连接层相比，它主要有两个优势：

一是全连接层把图像展平成一个向量，在输入图像上相邻的元素可能因为展平操作不再相邻，网络难以捕捉局部信息。而卷积层的设计，天然地具有提取局部信息的能力。

二是卷积层的参数量更少。不考虑偏置的情况下，一个形状为 (ci,co,h,w) 的卷积核的参数量是 ci×co×h×w ，与输入图像的宽高无关。假如一个卷积层的输入和输出形状分别是 (c1,h1,w1) 和 (c2,h2,w2) ，如果要用全连接层进行连接，参数数量就是 c1×c2×h1×w1×h2×w2 。使用卷积层可以以较少的参数数量来处理更大的图像。

卷积层的简洁实现

pytorch 中nn.Conv2d 可以简单实现 主要注意下面几个参数
in_channels (python:int) – Number of channels in the input imag
out_channels (python:int) – Number of channels produced by the convolution
kernel_size (python:int or tuple) – Size of the convolving kernel
stride (python:int or tuple, optional) – Stride of the convolution. Default: 1
padding (python:int or tuple, optional) – Zero-padding added to both sides of the input. Default: 0
bias (bool, optional) – If True, adds a learnable bias to the output. Default: True

forward函数的参数为一个四维张量，形状为 (N,Cin,Hin,Win) ，返回值也是一个四维张量，形状为 (N,Cout,Hout,Wout) ，其中 N 是批量大小， C,H,W 分别表示通道数、高度、宽度。

X = torch.rand(4, 2, 3, 5)
print(X.shape)

conv2d = nn.Conv2d(in_channels=2, out_channels=3, kernel_size=(3, 5), stride=1, padding=(1, 2))
Y = conv2d(X)
print('Y.shape: ', Y.shape)
print('weight.shape: ', conv2d.weight.shape)
print('bias.shape: ', conv2d.bias.shape)

输出结果
torch.Size([4, 2, 3, 5])
Y.shape: torch.Size([4, 3, 3, 5])
weight.shape: torch.Size([3, 2, 3, 5])
bias.shape: torch.Size([3])

池化

池化层主要用于缓解卷积层对位置的过度敏感性。同卷积层一样，池化层每次对输入数据的一个固定形状窗口（又称池化窗口）中的元素计算输出，池化层直接计算池化窗口内元素的最大值或者平均值，该运算也分别叫做最大池化或平均池化。图6展示了池化窗口形状为 2×2 的最大池化。

池化有最大层池化和平均池化，简单点讲就是池化核覆盖的输入数组的最大值或平均值。

池化层的简洁实现

我们使用Pytorch中的nn.MaxPool2d实现最大池化层，关注以下构造函数参数：

kernel_size – the size of the window to take a max over
stride – the stride of the window. Default value is kernel_size
padding – implicit zero padding to be added on both sides
forward函数的参数为一个四维张量，形状为 (N,C,Hin,Win) ，返回值也是一个四维张量，形状为 (N,C,Hout,Wout) ，其中 N 是批量大小， C,H,W 分别表示通道数、高度、宽度。

X = torch.arange(32, dtype=torch.float32).view(1, 2, 4, 4)
pool2d = nn.MaxPool2d(kernel_size=3, padding=1, stride=(2, 1))
Y = pool2d(X)
print(X)
print(Y)

输出结果
tensor([[[[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[12., 13., 14., 15.]],

     [[16., 17., 18., 19.],
      [20., 21., 22., 23.],
      [24., 25., 26., 27.],
      [28., 29., 30., 31.]]]])

tensor([[[[ 5., 6., 7., 7.],
[13., 14., 15., 15.]],

     [[21., 22., 23., 23.],
      [29., 30., 31., 31.]]]])

平均池化层使用的是nn.AvgPool2d，使用方法与nn.MaxPool2d相同