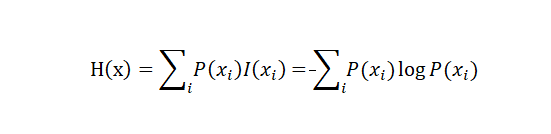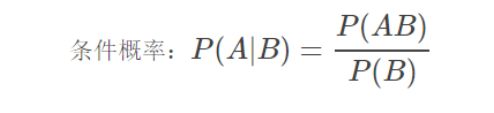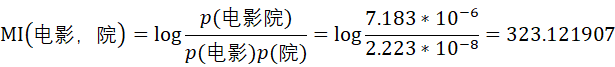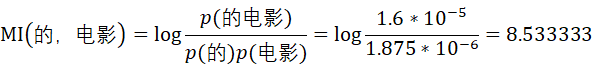NLP之通过词频发现中文新词

新词发现

新词发现任务是中文自然语言处理的重要步骤。新词有“新”就有“旧”，属于一个相对个概念，在相对的领域（金融、医疗），在相对的时间（过去、现在）都存在新词。文本挖掘会先将文本分词，而通用分词器精度不过，通常需要添加自定义字典补足精度，所以发现新词并加入字典，成为文本挖掘的一个重要工作。

这个和 HMM 发现未登录词还有区别，HMM 根据已有的经验去判断一些新词，或者没有统计过的。 词频统计是根据 在一篇文章中 两个单词 出现的 次数 和频率来判断，比如一个新词 豆腐 ，在文章中豆和腐 两个词反复出现 我们就认为他们是一个不可分的单词。

文本片段

我们将文章每一句话 ，每一个字 给切开

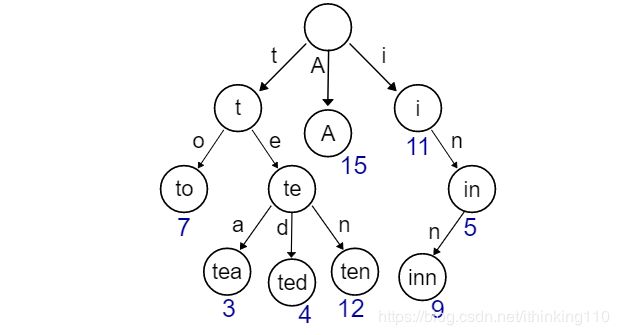
文本片段，最常用的方法就是n元语法(ngram) （后面我们会详细讲解），将分本分成多个n长度的文本片段。数据结构，这里采用Trie树的方案，这个方案是简单容易实现，而且用Python的字典做Hash索引实现起来也很优美，唯独的一个问题是所有的数据都存在内存中，这会使得内存占用量非常大，如果要把这个工程化使用，还需要采用其他方案，比如硬盘检索 ，ES。

trie 树：

我们先将文章切分成句子，每一个句子 根据 ngram 规则 我们会 拆解。
比如6元 ngram： 新词发现任务是中文自然语言处理的重要步骤

新词发现任务

词发现任务是

发现任务是中

现任务是中文 …

等等这样的句子 直到结尾。

在将这样的 6元 ngram 插入 到字典中。

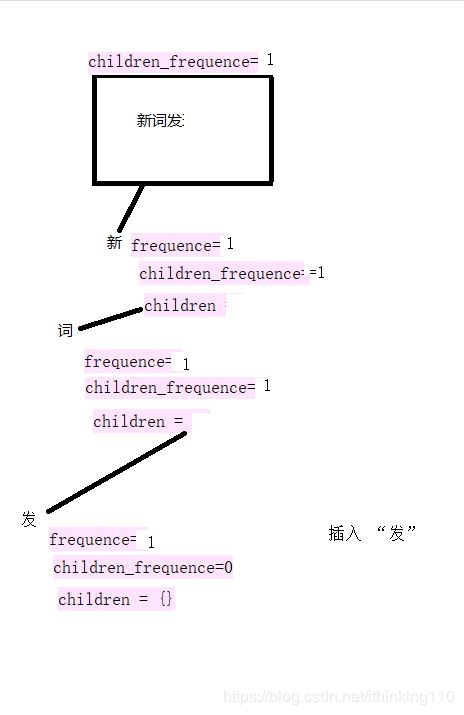
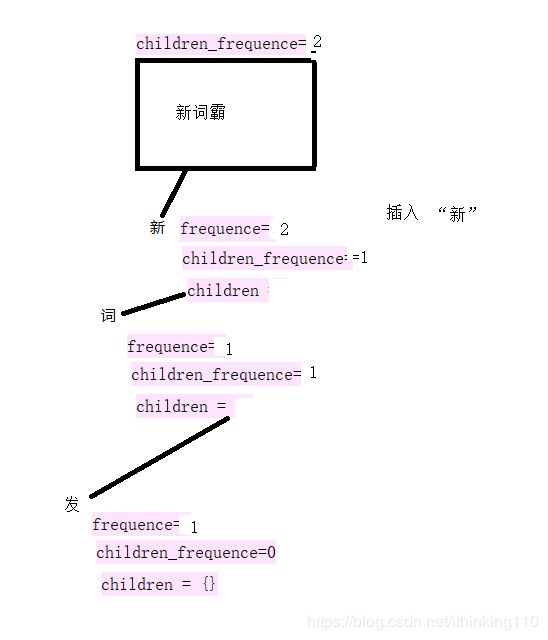
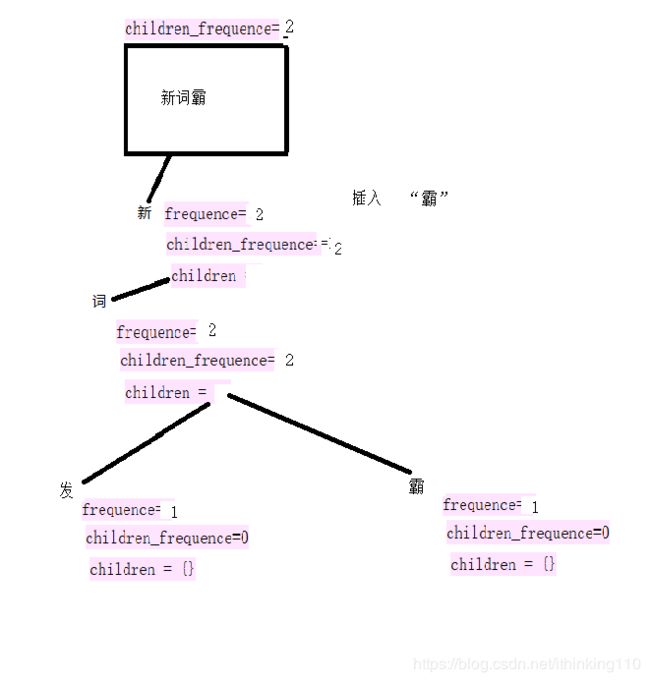
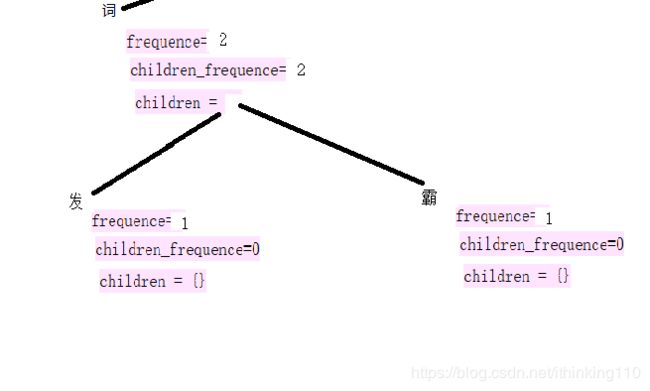
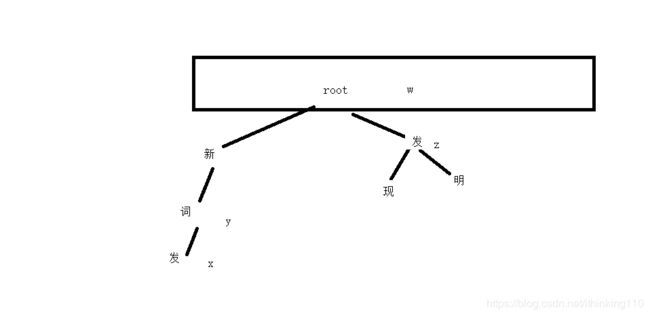
比如我们要插入一个句子 ： 新词发，新词霸 。

注意：下面的 每一个开始节点都叫root 节点也就是同一个节点，为了表示明白 标记了不同的句子。

插入 新：

在插入一个句子 ： 新词霸。

代码实现

class TrieNode(object):
    def __init__(self, 
                 frequence=0, 
                 children_frequence=0, 
                 parent=None):

        self.parent = parent
        self.frequence = frequence
        self.children = {} 
        self.children_frequence = children_frequence

    def insert(self, char):
        self.children_frequence += 1
        self.children[char] = self.children.get(char, TrieNode(parent=self))
        self.children[char].frequence += 1
        return  self.children[char]
        
    def fetch(self, char):
        return self.children[char]
    
class TrieTree(object):
    def __init__(self, size=6):
        self._root = TrieNode()
        self.size = size
        
    def get_root(self):
        return self._root
    
    def insert(self, chunk):
        node = self._root
        for char in chunk:
            node = node.insert(char)
        if len(chunk) < self.size:
            # add symbol "EOS" at end of line trunck
            node.insert("EOS")

    def fetch(self, chunk):
        node = self._root
        for char in chunk:
            node = node.fetch(char)
        return node

Trie树的结构上，我添加了几个参数，parent，frequence，children_frequence，他们分别是：

parent，当前节点的父节点，如果是“树根”的时候，这个父节点为空；
frequence，当前节点出现的频次，在Trie树上，也可以表示某个文本片段的频次，比如"中国"，“国”这个节点的frequence是100的时候，“中国”俩字也出现了100次。这个可以作为最后的词频过滤用。
children_frequence，当前接点下有子节点的"frequence"的总和。比如在刚才的例子上加上“中间”出现了99次，那么“中”这个节点的children_frequence的值是199次。 这样的构造让第二部分的计算更加方面。
这个任务中需要构建两棵Trie树，表示正向和反向两个字符片段集。

计算自由度

自由度，使用信息熵构建文本片段左右熵。熵越大，表示该片段与左右邻字符相互关系的不稳定性越高，那么越有可能作为独立的片段使用

其中，I(x)表示x的自信息 。

比如

比如 新词发现任务 这句话 。

1， 先 正向拆解。

会拆解成 ：

新词发现任’, ‘新词发现’, ‘新词发’, ‘新词’, ‘词发现任务’, ‘词发现任’, ‘词发现’, ‘词发’, ‘发现任务’, ‘发现任’, ‘发现’, ‘现任务’, ‘现任’, '任务

分别计算 自由度：
新词发现任 和 dict_keys([‘务’])
词发现任 和 dict_keys([‘务’])
发现任 和 dict_keys([‘务’])
现任 和 dict_keys([‘务’])

2， 倒着拆解

任现发词新’, ‘现发词新’, ‘发词新’, ‘词新’, ‘务任现发词’, ‘任现发词’, ‘现发词’, ‘发词’, ‘务任现发’, ‘任现发’, ‘现发’, ‘务任现’, ‘任现’, '务任

务任现发词 和 dict_keys([‘新’]) 自由度
任现发词 和 dict_keys([‘新’]) 自由度
现发词 和 dict_keys([‘新’]) 自由度
发词 和 dict_keys([‘新’]) 自由度

3，计算公式：

对于 比如上图中 新词发 计算 发和 新词的自由度 。

-(1/2) log( 1/2) + -(1/2) log( 1/2)

凝固度

用信息论中的互信息表示，在概率论中，如果x跟y不相关，则p(x,y)=p(x)p(y)。二者相关性越大，则p(x,y)就相比于p(x)p(y)越大。用后面的式子可能更好理解，在y出现的情况下x出现的条件概率p(x|y)除以x本身出现的概率p(x)，自然就表示x跟y的相关程度。

举例：

因此，我们利用人人网用户状态语料分别对“的电影”和“电影院”的互信息进行计算。

在2400万字的数据中，“电影”出现的次数为2774次，出现的概率为

院”字出现的次数为4797次，出现的概率为

若“电影”和“院”之间毫无关系，那么根据条件独立性假设，预测“电影”与“院”拼接在一起的概率应为

但事实上，“电影院”在语料中出现的次数为175次，出现的概率为

由此可计算“电影”和“院”的互信息为

类似的，可得到“的”出现的的概率为

预测“的”与“电影”拼接在一起的概率应为

而事实上，“的电影”在语料中出现的概率为

由此可计算“的”和“电影”的互信息为

根据统计学知识，互信息值越高，表明X和Y的相关性越高，则X和Y组成词语的可能性越大；反之，互信息值越低，X和Y之间相关性越低，则X和Y之间存在边界的可能性越大。

因此，由上述计算结果可知，

因此，“电影院”更可能是一个词语，而“的电影”更可能是“的”和“电影”这两个片段偶然拼接在一起的。

文本中

求 P(发| 新词) = x/y p( 发 )= z/ w

新词发 = log ( P(发| 新词) / p( 发 ) )

代码

def calc_mutualinfo(chunks, ngram):
    """计算互信息
    Args:
        chunks，是所有数据的文本片段
        ngram，是Trie树
    Return:
        word2mutualinfo，返回一个包含每个chunk和对应互信息的字典。
    """
    def parse(chunk, root):
        sub_node_y_x = ngram.fetch(chunk)
        node = sub_node_y_x.parent
        sub_node_y = root.children[chunk[-1]]

        # 这里采用互信息log(p(y|x)/p(y))的计算方法
        prob_y_x = float(sub_node_y_x.frequence) / node.children_frequence
        prob_y = float(sub_node_y.frequence) / root.children_frequence
        mutualinfo = math.log(prob_y_x / prob_y)
        return mutualinfo, sub_node_y_x.frequence

    word2mutualinfo = {}  
    root = ngram.get_root()
    for chunk in chunks:
        word2mutualinfo[chunk] = parse(chunk, root)
    return word2mutualinfo

过滤：

最终计算得出互信息、信息熵，甚至也统计了词频，最后一步就是根据阈值对词进行过滤。

根据前面得出的 各种结果 去过滤

k== 新词发现任 0.0
k== 新词发现 0.0
k== 新词发 0.0
k== 新词 0.0
k== 词发现任务 0.0
k== 词发现任 0.0
k== 词发现 0.0
k== 词发 0.0
k== 发现任务 0.0

代码实现

def _fetch_final(fw_entropy，
                 bw_entropy,
                 fw_mi,
                 bw_mi
                 entropy_threshold=0.8,
                 mutualinfo_threshold=7,
                 freq_threshold=10):
        final = {}
        for k, v in fw_entropy.items():
            last_node = self.fw_ngram
            if k[::-1] in bw_mi and k in fw_mi:
                mi_min = min(fw_mi[k][0], bw_mi[k[::-1]][0])
                word_prob = min(fw_mi[k][1], bw_mi[k[::-1]][1])
                if mi_min < mutualinfo_threshold:
                    continue
            else:
                continue
            if word_prob < freq_threshold:
                 continue
            if k[::-1] in bw_entropy:
                en_min = min(v, bw_entropy[k[::-1]])
                if en_min < entropy_threshold:
                    continue
            else:
                continue
            final[k] = (word_prob, mi_min, en_min)
        return final

下载地址：

参考文献

http://www.flykun.com/%E8%AF%8D%E9%A2%91%E3%80%81%E4%BA%92%E4%BF%A1%E6%81%AF%E3%80%81%E4%BF%A1%E6%81%AF%E7%86%B5%E5%8F%91%E7%8E%B0%E4%B8%AD%E6%96%87%E6%96%B0%E8%AF%8D/

https://blog.csdn.net/sophiezjz/article/details/84024020