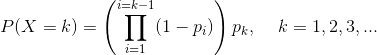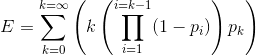python-几何分布（scipy.stats.geom）
一、摘要
几何分布很简单，描述的是重复进行伯努利试验，直到成功一次时进行的试验次数n的概率分布。例如掷骰子直到1点向上时所进行的试验次数。几何分布是离散型概率分布，要么就试验1次时成功，要么2次时成功，...。没有1.5次时成功的说法 。
二、几何分布公式
几何分布概率分布列为：
其中p表示一次试验成功的概率。
期望:
, 方差:
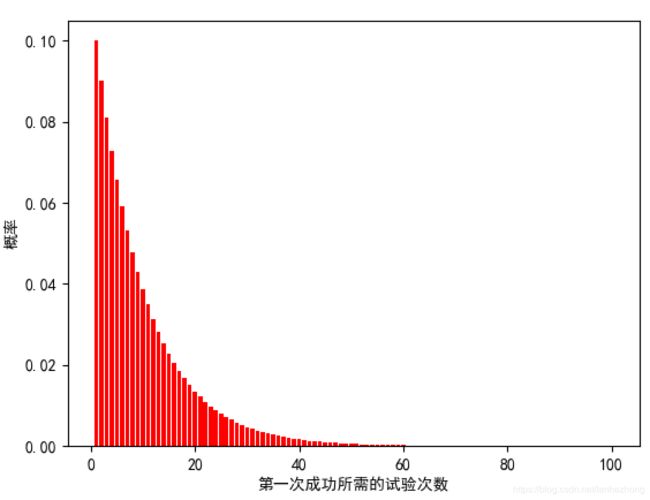
三、概率直方图(python计算)：
from scipy import stats
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']#用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False#用来正常显示负号
p=0.1
X = []
Y=[]
for x in np.linspace(1, 100, 100):
X.append(x)
# Y.append((1-p)**(x-1)*p) #公式计算
Y.append(stats.geom.pmf(x, p)) #stats.geom工具计算
plt.bar(X, Y, color="red")
plt.xlabel("第一次成功所需的试验次数")
plt.ylabel("概率")
plt.show()
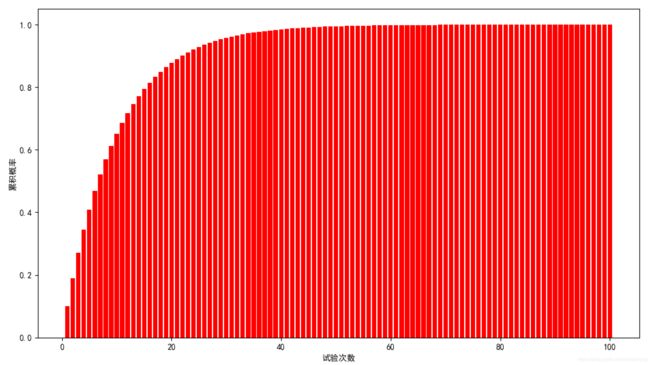
四、累积概率分布
用scipy.stats.geom.cdf(k, p)计算k之前（包括k）的累积概率
from scipy import stats
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']#用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False#用来正常显示负号
p=0.1
X = []
Y=[]
for x in np.linspace(1, 100, 100):
X.append(x)
Y.append(stats.geom.cdf(x, p)) #stats.geom工具计算
plt.bar(X, Y, color="red")
plt.xlabel("试验次数")
plt.ylabel("累积概率")
plt.show()
五、对p的延伸
如果p并不是每次都一样，也就是每次试验成功的概率并不完全相等，可以对公式进行改造。
相应的也可以计算期望
根据期望计算公式，现实中由于样本有限，我们可能并没有k 接近无穷时的概率。假设我们只有n个概率样本
,这里有2种方法估计期望：
（1）、取
作为平均每次发生的概率，由此计算期望
（2）、由于我们没有更多的样本，不妨假设未来一直按样本重复着，，，...，由此计算期望
(注意看分子最后2项，最后一项没有p)
公式推导过程可以看：几何分布每次概率不同期望公式推导（多个不同p的几何分布期望）
问题：
1、某摇号系统，每月摇号一次，由于摇号人数不固定，每个月摇号的中签率不固定。现收集到历史连续24个月摇号中签概率分别为：
0.0023, 0.0030, 0.0031, 0.0035, 0.0029, 0.0022, 0.0024, 0.0040, 0.0026, 0.0035, 0.0028, 0.0029,
0.0038, 0.0033, 0.0027, 0.0042, 0.0058, 0.0035, 0.0025, 0.0028, 0.0035, 0.0033, 0.0032, 0.0041
问：一个人从现在开始摇号直到中签的期望月数是多少？
方法（1）：，p=0.0032458, E=308.087。
方法（2）：
结果E=308.638
到这里，我终于知道为何摇号我总是没有中签。