FM算法python实现

在计算广告中，CTR预估(click-through rate)是非常重要的一个环节，对于特征组合来说，FM（因子分解机）是其中较为经典且被广泛使用的模型。
1、FM原理
=>重点内容解决稀疏数据下的特征组合问题

1. 可用于高度稀疏数据场景
2. 具有线性的计算复杂度

     对于categorical(类别)类型特征，需要经过One-Hot Encoding转换成数值型特征。CTR/CVR预测时，用户的性别、职业、教育水平、品类偏好，商品的品类等，经过One-Hot编码转换后都会导致样本数据的稀疏性。特别是商品品类这种类型的特征，如商品的末级品类约有550个，采用One-Hot编码生成550个数值特征，但每个样本的这550个特征，有且仅有一个是有效的（非零）。由此可见，经过One-Hot编码之后，大部分样本数据特征是比较稀疏的(即特定样本的特征向量很多维度为0)，同时导致特征空间大。(对于每一个特征，如果它有m个可能值，那么经过独热编码后，就变成了m个二元特征(取值0或1)。并且，这些特征互斥，每次只有一个激活。因此，数据会变成稀疏的.) sklearn中preprocessing.OneHotEncoder实现该编码方法。
     通过观察大量的样本数据可以发现，某些特征经过关联之后，与label之间的相关性就会提高。例如，“USA”与“Thanksgiving”、“China”与“Chinese New Year”这样的关联特征，对用户的点击有着正向的影响。换句话说，来自“China”的用户很可能会在“Chinese New Year”有大量的浏览、购买行为，而在“Thanksgiving”却不会有特别的消费行为。这种关联特征与label的正向相关性在实际问题中是普遍存在的，如“化妆品”类商品与“女”性，“球类运动配件”的商品与“男”性，“电影票”的商品与“电影”品类偏好等。因此，引入两个特征的组合是非常有意义的。(我的理解：个性化特征)

一般的线性模型为：

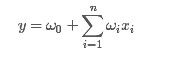
从上面的式子很容易看出，一般的线性模型压根没有考虑特征间的关联(组合)。为了表述特征间的相关性，我们采用多项式模型。在多项式模型中，特征xi与xj的组合用xixj表示。为了简单起见，我们讨论二阶多项式模型。具体的模型表达式如下：
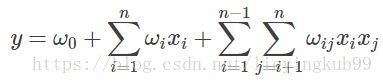(1)
上式中，n表示样本的特征数量,xi表示第i个特征。
与线性模型相比，FM(Factorization Machine)的模型就多了后面特征组合的部分。
从公式(1)可以看出，组合特征的参数一共有 n(n−1)/2 个，任意两个参数都是独立的。然而，在数据稀疏性普遍存在的实际应用场景中，二次项参数的训练是很困难的。其原因是，每个参数 wij 的训练需要大量 xi 和xj都非零的样本；由于样本数据本来就比较稀疏，满足“xi 和 xj 都非零”的样本将会非常少。训练样本的不足，很容易导致参数 wij 不准确，最终将严重影响模型的性能。
类似地，所有二次项参数W i,j可以组成一个对称阵W,那么这个矩阵就可以分解为 W=VVT,V的第i行便是第i维特征的隐向量，则FM的模型方程为：

2、FM交叉项求解过程

对表达式进行化简，可以把时间复杂度降低到O(kn)
第一步是一个矩阵(矩阵中所有元素求和)减去对角线部分，然后除以2。多项式部分的计算复杂度是O(kn).即FM可以在线性时间对新样本作出预测

3、实现步骤

代码简单实现：

添加依赖项：

from __future__ import division
from math import exp
import pandas as pd
from numpy import *
from random import normalvariate
from datetime import datetime
from sklearn import preprocessing

读取数据：

def load_train_data(data):
    global min_max_scaler
    data = pd.read_csv(data)
    labelMat = data.ix[:,-1]* 2 - 1
    X_train = np.array(data.ix[:, :-1])
    min_max_scaler = preprocessing.MinMaxScaler()
    X_train_minmax = min_max_scaler.fit_transform(X_train)
    return X_train_minmax,labelMat

def laod_test_data(data):

    data = pd.read_csv(data)
    labelMat = data.ix[:, -1] * 2 - 1
    X_test = np.array(data.ix[:, :-1])
    X_tset_minmax = min_max_scaler.transform(X_test)
    return X_tset_minmax, labelMat

定义sigmod函数：

def sigmoid(inx):
    return 1. / (1. + exp(-max(min(inx, 10), -10)))

模型训练：

def FM_function(dataMatrix, classLabels, k, iter):
    m, n = shape(dataMatrix)
    alpha = 0.01
    w = zeros((n, 1))
    w_0 = 0.
    v = normalvariate(0, 0.2) * ones((n, k))
    for it in xrange(iter):
        print it
        for x in xrange(m):
            inter_1 = dataMatrix[x] * v
            inter_2 = multiply(dataMatrix[x], dataMatrix[x]) * multiply(v, v)
            interaction = sum(multiply(inter_1, inter_1) - inter_2) / 2.
            p = w_0 + dataMatrix[x] * w + interaction  #
            loss = sigmoid(classLabels[x] * p[0, 0]) - 1
            w_0 = w_0 - alpha * loss * classLabels[x]
            for i in xrange(n):
                if dataMatrix[x, i] != 0:
                    w[i, 0] = w[i, 0] - alpha * loss * classLabels[x] * dataMatrix[x, i]
                    for j in xrange(k):
                        v[i, j] = v[i, j] - alpha * loss * classLabels[x] * (
                        dataMatrix[x, i] * inter_1[0, j] - v[i, j] * dataMatrix[x, i] * dataMatrix[x, i])

    return w_0, w, v

精确度计算及其评估Assessment：

def Assessment(dataMatrix, classLabels, w_0, w, v):
    m, n = shape(dataMatrix)
    allItem = 0
    error = 0
    result = []
    for x in xrange(m):
        allItem += 1
        inter_1 = dataMatrix[x] * v
        inter_2 = multiply(dataMatrix[x], dataMatrix[x]) * multiply(v, v)
        interaction = sum(multiply(inter_1, inter_1) - inter_2) / 2.
        p = w_0 + dataMatrix[x] * w + interaction
        pre = sigmoid(p[0, 0])
        result.append(pre)
        if pre < 0.5 and classLabels[x] == 1.0:
            error += 1
        elif pre >= 0.5 and classLabels[x] == -1.0:
            error += 1
        else:
            continue
    print result
    return float(error) / allItem

main函数：

if __name__ == '__main__':
    #-------读取数据----------
    trainData = 'train.txt'
    testData = 'test.txt'
    #------模型训练----
    dataTrain, labelTrain = load_train_data(trainData)
    dataTest, labelTest = laod_test_data(testData)
    w_0, w, v = FM_function(mat(dataTrain), labelTrain, 15, 100)

参考资料：
1. https://blog.csdn.net/jediael_lu/article/details/77772565#1fm
2. https://www.jianshu.com/p/55be900e18db
3. http://baijiahao.baidu.com/s?id=1589879343345420975&wfr=spider&for=pc
4. https://blog.csdn.net/g11d111/article/details/77430095