python计算线段夹角
计算两条线段之间的夹角
1. 问题与解决思路
如上图所示,要求图中线段AB,CD之间的夹角(AB,CD都没有方向),可以按照如下步骤计算:
- 计算AB线段与X轴的夹角.
- 计算CD线段与Y轴的夹角.
- 合并两个夹角,因为求的是最小角度,所以需要对180进行求余,得到的角度为最后结果.
2. 具体步骤
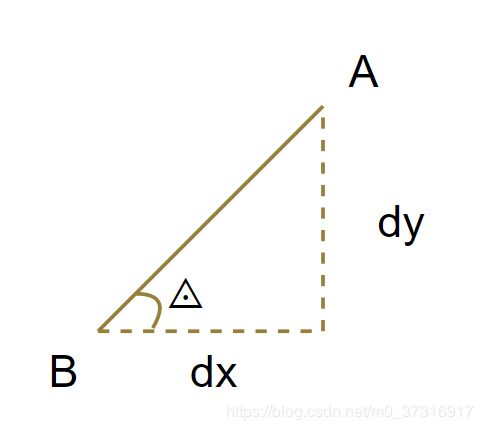
首先计算出AB线段与X轴的夹角,将AB线段进行分解,如下图:
其中角度的计算公式为
◬=arctan(dy/dx)
同理求得CD线段与X轴的角度,这里存在一个问题,由于线段不是向量,因此角度可能为60°,也可能为360°-60°=300°,因此后续合并两个角度的时候需要解决这个问题.
合并的原理也比较简单,由于用python的math.atan2(y,x)函数计算线段与X轴夹角,返回的角度在[-180,180],也就是说在1,2象限为正数,3,4象限为负数,在合并两个夹角时考虑正负号,计算完成后再对180°求余即可.
1.3 代码
import math
class Point:
"""
2D坐标点
"""
def __init__(self, x, y):
self.X = x
self.Y = y
class Line:
def __init__(self, point1, point2):
"""
初始化包含两个端点
:param point1:
:param point2:
"""
self.Point1 = point1
self.Point2 = point2
def GetAngle(line1, line2):
"""
计算两条线段之间的夹角
:param line1:
:param line2:
:return:
"""
dx1 = line1.Point1.X - line1.Point2.X
dy1 = line1.Point1.Y - line1.Point2.Y
dx2 = line2.Point1.X - line2.Point2.X
dy2 = line2.Point1.Y - line2.Point2.Y
angle1 = math.atan2(dy1, dx1)
angle1 = int(angle1 * 180 / math.pi)
# print(angle1)
angle2 = math.atan2(dy2, dx2)
angle2 = int(angle2 * 180 / math.pi)
# print(angle2)
if angle1 * angle2 >= 0:
insideAngle = abs(angle1 - angle2)
else:
insideAngle = abs(angle1) + abs(angle2)
if insideAngle > 180:
insideAngle = 360 - insideAngle
insideAngle = insideAngle % 180
return insideAngle
if __name__ == '__main__':
L1 = Line(Point(0, 0), Point(-2, 0))
L2 = Line(Point(0, 0), Point(2, 0))
res = GetAngle(L1, L2)
print(res) # 结果为0°