排序算法---快速排序,随机快速排序和双路快排(python版)
1、什么是快速排序算法?
快速排序是由东尼·霍尔所发展的一种排序算法,速度快,效率高,也是实际中最常用的一种算法,被称为20世纪对世界影响最大的算法之一。
基本思想:
1): 从序列中挑出一个元素作为"基准"元素,一般是该序列的第一个元素或者是最后一个元素。
2): 把序列分成2个部分,其数值大于"基准"元素的元素放在"基准"元素的左边,否在放在"基准"元
素的右边,此时"基准"元素所在的位置就是正确的排序位置,这个过程被称为 partition(分区)。
3): 递归将"基准"元素左边的序列和"基准"元素右边的序列进行partition操作。
2、算法的演示
这个就是待排序的数组序列,第一个元素作为"基准"元素
给"基准"元素找到合适的位置,将比"基准"元素小的元素放在其左边,否则放在其右边
至此这个序列就成了这样了,这个过程成为partition
下面来看看partition的具体实现过程:
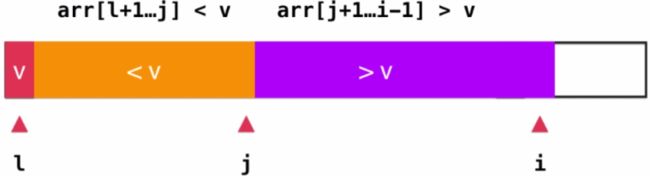
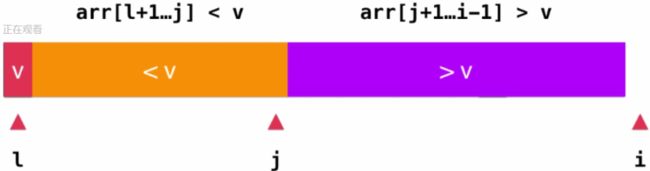
将"基准"元素用v表示,使用i作为遍历序列的索引值,j的位置表示>v部分和 如果此时i指向的元素大于v,这个好处理,直接将i++即可,也就表示大于v的元素多了一个 如果此时i指向的元素小于v,那么需要将i指向的元素与大于v序列的第一个元素交换位置,即swap(arr[i], arr[j+1]),然后再将i++,再将j++即可,表示小于v的元素多了一个。如下图所示 进行swap(arr[i], arr[j+1]) j++ i++ 由此可知,当遍历完成之后,就会出现这样的效果,然后我们只需将元素v与j指向的元素交换位置即可 此时就出现了小于"基准"元素的元素在其左边,大于"基准"元素的元素在其右边的分布情况。 3. 普通单路快排特点: 1)普通快速排序最差时间复杂度为o(n^2) 2)期望时间复杂度为o(nlgn) 3)在o(nlgn)中蕴含的常量比较小 4)就地排序,不需要辅助数组空间 改进一,随机单路快排: 那什么时候普通快速排序算法的最差时间复杂度会下降为o(n^2)呢? 我们可以想象一种情况,当待排序的数组近乎有序时,因为我们选择第一个元素作为基准,这时导致比基准元素小的元素基本为0,导致元素全部在基准一边。这样就导致我们递归算法的深度由期望的log(n),变为n。因此算法时间复杂度退化为o(n^2)级别。 那么这种情况的解决办法就是: 尽可能的别让第一个元素成为"基准"元素,而最好使用中间位置的元素成为 "基准"元素,那如何做到这点呢?解决办法就是"基准"元素随机产生,而不指定。请看下面的代码(只用修改_partition()): 改进二,双路快排: 之前讲的,当我们排序的是一个近乎有序的序列时,快速排序会退化到一个O(n^2)级别的排序算法, 而对此的改进就是引入了随机化快速排序算法;但是当我们排序的是一个数值重复率非常高的序列时, 此时随机化快速排序算法就不再起作用了,而将会再次退化为一个O(n^2)级别的排序算法,那为什么 会出现这种情况呢?且听下面的分析: 如上图所示就是之前分析的快速排序算法的partition的操作原理,我们通过判断此时i索引指向的数组 元素e>v还是 但是这里其实我们是没有考虑=v的情况,其实隐含的意思就是下面的两种情况: 其实从这里就可以看出来了,不管是>=v还是<=v,当我们的序列中存在大量重复的元素时, 排序完成之后就会将整个数组序列分成两个极度不平衡的部分,所以又退化到了O(n^2)级别 的时间复杂度,这是因为对于每一个"基准"元素来说,重复的元素太多了,如果我们选的"基准" 元素稍微有一点的不平衡,那么就会导致两部分的差距非常大;即时我们的"基准"元素选在了 一个平衡的位置,但是由于等于"基准"元素的元素也非常多,也会使得序列被分成两个及其不平 衡的部分,那么在这种情况下快速排序就又会退化成O(n^2)级别的排序算法。如何解决呢? 这就要用到今天讲的双路快速排序算法的原理了。 双路快速排序算法的原理 之前说的快速排序算法是将>v和 的双路快速排序算法则不同,他使用两个索引值(i、j)用来遍历我们的序列,将 引i所指向位置的左边,而将>v的元素放在索引j所指向位置的右边,这也正是双路排序算法的 partition原理: 基本思想: 首先从左边的i索引往右边遍历,如果i指向的元素 然后使用j索引从右边开始往左边遍历,如果j指向的元素>v,那直接将j--移动到下一个位置,直道j指向的元素<=v则停止 此时i之前的元素都已经归并为 这样就可以避免出现=v的元素全部集中在某一个部分,这正是双路排序算法的一个核心 将i++,j--开始遍历后后面的元素 代码 : tips: 讨论: 比如数组 1,0,0, ..., 0, 0 a. 对于arr[i] b. 对于arr[i]<=stand和arr[j]>=stand的方式,第一次partition得到的分点是数组的倒数第二个。 这是因为对于连续出现相等的情况,a方式会交换i和j的值;而b方式则会将连续出现的这些值归为其中一方,使得两棵子树不平衡 http://coding.imooc.com/learn/questiondetail/4920.html def _partition(arr, l, r):
tag = arr[l]
j = l + 1
for i in range(l+1, r+1):
if arr[i] < tag:
arr[i], arr[j] = arr[j], arr[i]
j += 1
arr[j-1], arr[l] = arr[l], arr[j-1]
return j - 1
def _quick_sort(arr, l, r):
if l < r:
p = _partition(arr, l, r)
_quick_sort(arr, l, p-1)
_quick_sort(arr, p+1, r)
def quick_sort(arr, nums):
l, r = 0, nums-1
_quick_sort(arr, l, r)def _partition_random(arr, l, r):
ind = random.randint(l, r)
arr[l], arr[ind] = arr[ind], arr[l]
tag = arr[l]
j = l + 1
for i in range(l+1, r+1):
if arr[i] < tag:
arr[i], arr[j] = arr[j], arr[i]
j += 1
arr[j-1], arr[l] = arr[l], arr[j-1]
return j - 1def insert_sort(arr, l, r):
for i in range(l+1, r+1):
j = i - 1
temp = arr[i]
if arr[i] < arr[j]:
while j >= 0 and arr[j] > temp:
arr[j+1] = arr[j]
j -= 1
arr[j+1] = temp
def _partition_doubule(arr, l, r):
ind = random.randint(l, r)
arr[l], arr[ind] = arr[ind], arr[l]
stand = arr[l]
i, j = l+1, r
while True:
while i <= r and arr[i] < stand: #不能改为arr[i] <= stand, 原因下文有讲解
i += 1
while j >= l+1 and arr[j] > stand: #不能改为arr[j] >= stand.
j -= 1
if i > j:
break
else:
arr[i], arr[j] = arr[j], arr[i]
i += 1
j -= 1
arr[j], arr[l] = arr[l], arr[j]
return j
def _quick_sort(arr, l, r):
if (r - l) < 15: #当待排序元素个数小于15时改为插入排序,可提高程序运行速度
insert_sort(arr, l, r)
return
p = _partition_doubule(arr, l, r)
_quick_sort(arr, l, p-1)
_quick_sort(arr, p+1, r)
def quick_sort(arr, nums):
_quick_sort(arr, 0, nums-1)