自动驾驶-神经网络介绍

神经网络

在自动驾驶系统中，车辆会通过摄像头和传感器不断收集周围环境的数据，并指导车辆完成相应动作。车辆的传感器主要完成探测周围物体位置及预测其运动趋势的任务，摄像头则完成对周围物体进行识别以及对交通标志进行分类的任务。摄像头在对图像分类过程中使用的算法是机器学习中的神经网络算法，本章主要介绍神经网络算法的相关概念。

本章首先介绍神经网络会用到的一些基础概念，包括线性回归，逻辑回归，代价函数，梯度下降，然后介绍神经网络模型，前向传播算法，反向传播算法和正则化下一章利用神经网络模型结合tensorflow工具完成对交通标志进行分类的实践。

Tom Mitchell给出的机器学习定义如下：“a computer program is said to learn from experience E, with respect to some task T, and some performance measure P, if its performance on T as measured by P improves with experience E.“即完成任务的过程中积累经验，得到一个能更好完成任务的程序或模型的过程。在实际的应用过程中，就是通过收集的包括自变量和因变量的数据集拟合一个函数，使得这个函数有新的自变量输入时，可以得到一个尽可能准确的结果。

线性回归

首先介绍最简单的线性模型，以使用房间面积作为特征，房价作为输出构建线性模型，

price=size∗weight+bias p r i c e = s i z e ∗ w e i g h t + b i a s

这个模型就是最简单的一元一次线性方程， 如图所示，

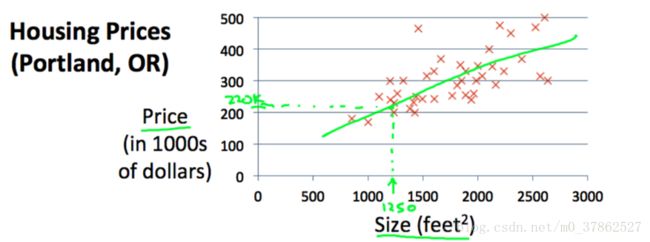
x号表示训练集，绿色实线是使用机器学习确定权重weight以后得到的线性模型。当有新的size输入时，使用训练得到的模型预测房价。

在机器学习中，一般将数据集中的自变量称为特征（feature），影响因子称为权重（weight），因变量称为标签（label）。利用数据集拟合线性方程的过程就称为线性回归。
当数据集有多个特征时，线性方程可以表示为：

h(w)=w1x1+w2x2+⋯+wnxn+b h ( w ) = w 1 x 1 + w 2 x 2 + ⋯ + w n x n + b

或

h(w)=∑i=1nwixi+b h ( w ) = ∑ i = 1 n w i x i + b

代价函数

为了衡量预测模型性能的优劣，引入代价函数，理论上只要表示预测值和真实值之间差异的函数都可以表示代价函数，例如线性方程常用的代价函数为：

J(w)=12m∑i=1m(h(w(i))−y(i))2 J ( w ) = 1 2 m ∑ i = 1 m ( h ( w ( i ) ) − y ( i ) )  2

逻辑回归使用的代价函数将在后边的小节给出。

梯度下降

当只有一个特征时，如下图所示，代价函数可以表示为一条以权重 θi θ i 为自变量，代价函数值为因变量的曲线，一种找到能够使代价函数值最小的 θ1 θ 1 的值的算法称为梯度下降算法，这种算法使用代价函数对权重求导数，找到能够使代价函数下降最快的 θ1 θ 1 的前进方向，在这一方向上更新 θ1 θ 1 的值，重新计算代价函数，求导，再更新……最终找到梯度为0时的 θ1 θ 1 的值。


推广导多元函数时，即对每个权重值 θi θ i 求偏导数，找到能使代价函数下降最快的权重的改变方向，更新，最终得可以得到代价函数的局部最小值。  如图所示，可以当作下山的不停计算当前位置梯度最大的方向并沿着这一方向前进一段距离，再重新计算梯度，前进最终到达山脚下的过程。更新权重值的公式为：

wi=wi−α∂∂wiJ(w) w i = w i − α ∂ ∂ w i J ( w )

其中 α α 称为**学习速率**，可以调节权重改变的速度，如果 α α 太小，则使训练速度下降，如果 α α 太大，则可能导致由于权重改变太快而不能到达最优值。

逻辑回归

线性回归的例子中，房价会随着面积的变化线性的变化。但是分类问题中，我们想要的结果并不能用数值大小来衡量，例如垃圾邮件的识别属于一个二值问题，我们想要的结果是利用模型判定一封邮件是否为垃圾邮件，其结果只有是和否两种选择。又例如交通标志的分类问题，利用模型得到的最终结果是判定给定的表示属于哪一类。得到处理这种分类问题的的模型的过程通常称为逻辑回归。

首先依然考虑一个特征的情况，我们以判定肿瘤为良性还是恶性的问题为例，如果以肿瘤大小作为模型的特征，当大于某一尺寸时，判定该肿瘤为恶性 y=1 y = 1 ，否则，判定为良性 y=0 y = 0

如下图所示，如果仍以线性方程作为模型，对于左边一条斜线，当 h(w)>0.5 h ( w ) > 0.5 时，则预测 y=1 y = 1 ，当 h(w)<0.5时 h ( w ) < 0.5 时 ，预测 y=0 y = 0 ，但当数据辆增加，拟合出的第二条曲线反而是模型的准确率下降，所以线性模型不适合应用在分类问题中。

为了解决分类问题，给出了逻辑回归方程,

hθ(x)=11+e−θTx h θ ( x ) = 1 1 + e − θ T x

如下图所示，逻辑回归的预测方程值在{0,1}之间，可以理解为该肿瘤为恶性肿瘤的概率。例如 hw(x)=0.7 h w ( x ) = 0.7 则判定该肿瘤为恶性肿瘤的概率为70%。


逻辑回归的代价函数的数学表示为：

J(w)=−1m[∑i=1my(i)loghw(x(i))+(1−y(i))log(1−hw(x(i)))] J ( w ) = − 1 m [ ∑ i = 1 m y ( i ) l o g h w ( x ( i ) ) + ( 1 − y ( i ) ) l o g ( 1 − h w ( x ( i ) ) ) ]

对逻辑回归方程使用梯度下降算法更新权值可以用如下方法表示：

wj=wj−α∑i=1m(hw(x(i))−y(i))x(i)j w j = w j − α ∑ i = 1 m ( h w ( x ( i ) ) − y ( i ) ) x j ( i )

多重分类问题

当分类超过三种时，通常使用one-vs-all的方法解决多重分类。one-vs-all方法是每次选取训练集中的一类作为预测目标，其他类归为另一类，将多类问题化为2类问题使用逻辑回归模型训练得到每一类的预测函数，对新的测试集，求解每一类预测函数对应的函数值，判定分类结果为函数值最高的预测函数对应的类。

以上就是机器学习最基本的一些概念，接下来介绍本章的终点，神经网络模型

神经网络

非线性方程能够通过对特征的组合解决一些分类问题，但是当特征太多时，非线性方程组合的种类急剧增加，例如在图像识别问题中，一副图像的每个像素点为一个特征，对于一个分辨率为64*64的图像来说，就有超过4k的特征，如果在对特征进行组合形成新的特征，那么就需要训练一个特征超过百万的预测模型。一般计算机无法承担如此巨大的训练任务。通过仿照人脑的工作原理，开发出一种新的训练模型称为神经网络或深度学习。以xor问题为例，数据集的对应关系为：

x1 x 1	x2 x 2	y
0	0	0
0	1	1
1	0	1
1	1	0

如果使用线性模型 hw(x)=w1x1+w2x2+b h w ( x ) = w 1 x 1 + w 2 x 2 + b 来拟合训练集,当代价函数最小时得到的权重值为 w1=0.5,w2=0.5 w 1 = 0.5 , w 2 = 0.5
无论输入什么样的测试集，预测值均为0.5，其预测结果并不理想。
xor可以表示为多种线性模型的组合例如:

AxorB=((AandB) or ((notA)and(notB))) A x o r B = ( ( A a n d B )   o r   ( ( n o t A ) a n d ( n o t B ) ) )

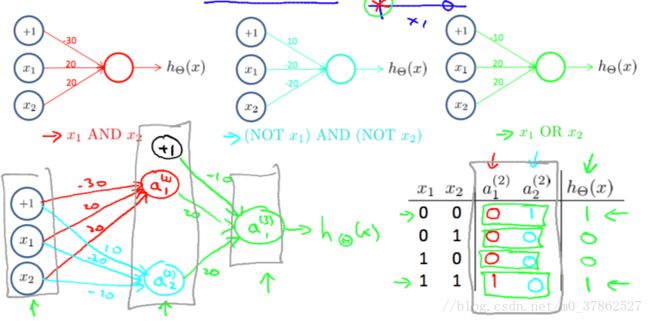
如图所示：在输入层与输出层之间添加一层隐藏层，首先输入层分别使用AND和 (NOTA)AND(NOTB) ( N O T A ) A N D ( N O T B ) 的逻辑回归方程得到第二层的节点，然后第二层节点再作为输入层，使用OR的逻辑回归方程得到输出层的节点。通过添加一个隐藏层实现了一个XOR的模型。

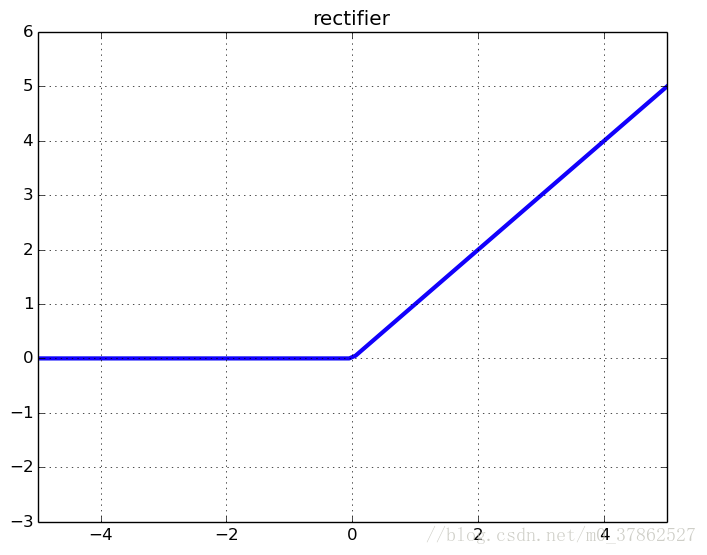
实际的神经网络网络和上边XOR的模型类似，只是在隐藏层优使用了依次激活函数，目前使用最多的激活函数称为整流线性单元（relu），齐函数形式为 g(z)=max{0,z} g ( z ) = m a x { 0 , z }

神经网络的代价函数与逻辑回归类似，
其中 θ θ 表示权重，m表示样本总量，K表示输出层的节点数，L表示神经网络的层数。 可以看出神经网络的代价函数形式和one-vs-all的分类模型的代价函数基本相同，区别仅是是增加了权重值的数量。

后向传播算法（backprob）

神经网络中使用梯度下降算法调整权重，更新权重的公式形式与前边介绍的梯度下降算法相同：

Θ(l)i,j=Θ(l)i,j−α∂∂Θ(l)i,jJ(Θ) Θ i , j ( l ) = Θ i , j ( l ) − α ∂ ∂ Θ i , j ( l ) J ( Θ )

由于神经网络是多层的，使用代价函数对前边的参数求偏导数时，需要使用链式法则将从代价函数到目标函数所经过的节点依次求导。
以下图为例， a a 表示每个节点的输出值，上标表示节点所在层，左下标对应前一层节点的位置，右下标对应右侧节点的位置，如果要计算代价函数对 Θ(3)11 Θ 11 ( 3 ) 的偏导数，其结果和逻辑回归模型计算偏导数的公式一致直接使用 ∂∂Θ(3)11JΘ(x) ∂ ∂ Θ 11 ( 3 ) J Θ ( x ) 计算偏导数，如果对 Θ(2)11 Θ 11 ( 2 ) 求偏导数时要使用链式法则，

∂∂Θ(2)1,1J(Θ)=∂J(Θ)∂a(3)1∂a(3)1∂Θ(2)1,1 ∂ ∂ Θ 1 , 1 ( 2 ) J ( Θ ) = ∂ J ( Θ ) ∂ a 1 ( 3 ) ∂ a 1 ( 3 ) ∂ Θ 1 , 1 ( 2 )

如果要继续对 Θ(1)11 Θ 11 ( 1 ) 求偏导数：

∂∂Θ(1)1,1J(Θ)=∂J(Θ)∂a(3)1∂a(3)1∂a(2)1∂a(2)1∂Θ(1)11 ∂ ∂ Θ 1 , 1 ( 1 ) J ( Θ ) = ∂ J ( Θ ) ∂ a 1 ( 3 ) ∂ a 1 ( 3 ) ∂ a 1 ( 2 ) ∂ a 1 ( 2 ) ∂ Θ 11 ( 1 )

对比两个公式可以发现其中 ∂J(Θ)∂a(3)1 ∂ J ( Θ ) ∂ a 1 ( 3 ) 使用了两次，当神经网络深度较大时这些重复计算量会极大的拖慢计算速度，所以在实际的神经网络训练过程中，还会被已经求出的偏导数保存起来，以牺牲一定存储空间的代价提高训练速度。

正则化

从神经网络的模型可以看出，从特征到预测值的计算过程中，经过大量的函数复合，会出现高次幂的特征，随着特征越来越复杂，会导致过拟合现象（overfitting）， 即随着训练时间的增长训练模型在训练集中准确度逐步提高，但是在测试集中的准确率反而下降。如下图所示，图一使用线性模型准确率较低，图二使用非线性模型准确率得到极大改善，图三虽然得到了准确的决策边界，但是使用测试集进行评估时，图三的表现低于图二，这是由于图三过多考虑训练集中的特殊情况，使得其泛化能力下降。

解决过拟合问题的方法之一是在代价函数中加入了正则项。如下图所示，加入正则项后逻辑函数和神经网络的代价函数修改为：

正则项是一种惩罚机制，当某个特征导致代价函数显著增加时，利用梯度下降算法可以使其对应的权重快速下降，削弱其在模型中的作用。

以逻辑回归的梯度下降算法为例，如上图所示，加入正则项的权重增加了一个小于1的系数，使其下降的更快。

以上就是对神经网络模型及其相关概念的介绍，本章主要是对吴恩达老师关于神经网络章节的学习总结，大量图片均出自老师的ppt, 有兴趣的同学可以学习老师的机器学习课程。下一章内容是使用神经网络模型解决自动驾驶系统中对交通标志分类。