自动驾驶-使用粒子滤波定位

前几章介绍了卡尔曼滤波是用来对其他车辆追踪和定位的，本章介绍的粒子滤波是用来定位自身的。通常我们用手机地图的gps功能已经能大致定位出自身位置，但是gps存在10m左右的偏差，这么大的偏差在自动驾驶时是无法承受的。本章介绍的粒子滤波是一种高精度定位自身位置的算法。

粒子滤波的原理概括来说是通过地图得到一些路标的坐标，假设自身车辆以某种概率分布在一定范围内，在这个范围内按概率分布假设一些粒子代表车辆位置，根据车辆运动情况预测每个粒子$\Delta t$以后的位置，车辆每隔$\Delta t$的时间还会用传感器感知路标相对自己的距离，用每个粒子周围路标的位置和传感器感知的路标位置做比较，传感器感知的路标和探测到的路标越接近则该粒子越有可能代表车辆位置。从预测到探测更新循环迭代，确认车辆的实际位置。

粒子滤波可以抽象为以下几步：

1. 初始化粒子
2. 预测
3. 探测更新
4. 重新分布粒子，重复2， 3步

下图是自动驾驶车辆使用粒子滤波的一般流程

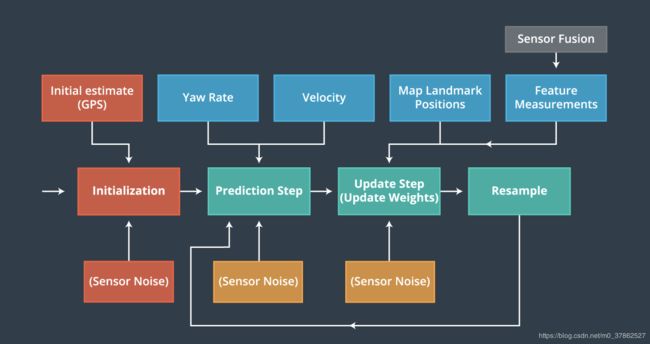
粒子滤波是一种比卡尔曼滤波更加简单的算法，下面对每一步进行更详细的说明并给出源码实现加深理解。

初始化粒子

第一步是撒粒子，但是粒子应该撒到什么位置呢？又该按什么规律撒呢？和其他传感器一样，gps数据应该也满足正态分布。所以先通过gps得到一个位置不精确的位置坐标$(x,y)$， 用正态分布的引擎以该位置为均值，以gps设备噪声为方差随机生成若干粒子。粒子数量是精度和计算时间的均衡，本次项目共生成300个粒子。对每个粒子依次编号，初始权重为1。

void ParticleFilter::init(double x, double y, double theta, double std[]) {
	// Set the number of particles. Initialize all particles to first position (based on estimates of 
    //   x, y, theta and their uncertainties from GPS) and all weights to 1. 
	// Add random Gaussian noise to each particle.
    Particle sample;
    default_random_engine gen;
    int particle_num = 300;
	// This line creates a normal (Gaussian) distribution for x
	normal_distribution dist_x(x, std[0]);
	// Create normal distributions for y and theta
	normal_distribution dist_y(y, std[1]);
	normal_distribution dist_theta(theta, std[2]);
	
	for (int i = 0; i < particle_num; ++i) {
		// Sample  and from these normal distrubtions like this: 
		//sample_x = dist_x(gen);
		//where "gen" is the random engine initialized earlier.
	    sample.id = i;	
		sample.x = dist_x(gen);
		sample.y = dist_y(gen);
		sample.theta = dist_theta(gen);
        sample.weight = 1.0;
        particles.push_back(sample);
        weights.push_back(1.0);
	}
    num_particles = particles.size();
    is_initialized = true;
}

预测

由于是定位自己的车辆，所以速度，方向都是已知量，根据状态方程计算$\Delta t$后每个粒子的位置即可，需要注意的是即使是自身速度和方向的值，也可能存在一定误差，所以每个粒子的预测值依然要考虑噪声影响。

void ParticleFilter::prediction(double delta_t, double std_pos[], double velocity, double yaw_rate) {
    std::random_device rd;
    std::mt19937 gen(rd());
    double x, y, theta;
    for (int i=0; i dist_x(x, std_pos[0]);
    	normal_distribution dist_y(y, std_pos[1]);
    	normal_distribution dist_theta(theta, std_pos[2]);
		particles[i].x = dist_x(gen);
		particles[i].y = dist_y(gen);
		particles[i].theta = dist_theta(gen);
        particles[i].id = i;
    }
    return;
}

更新粒子权重

我们将能代表特定坐标的物体称为路标（map_landmark），并且这些路标在地图中都是标明的，即坐标已知且精确。自身车辆通过传感器探测路标能得到一组变量，代表了某个路标和车辆的距离，我们逐个选取预测以后的粒子，以该粒子为坐标中心，就可以将距离变量映射到地图坐标中。映射以后的坐标和路标都在地图坐标系中可以相互比较，将距离最近传感器坐标和路标关联起来。

对每个粒子计算其探测到的路标和真实路标的位置差异的逆作为该粒子的权重。粒子的坐标位置和真实车辆的坐标位置越接近，则探测到的路标和真实路标位置也越接近，该粒子的权重就越大，反之相差越大权重越小。

对所有粒子权重归一化处理，使所有粒子权重值和为1.

double ParticleFilter::CalculateParticleWeight(double sensor_range, vector observations, Map map_landmarks, double sigma_x_2sq, double sigma_y_2sq, double outer_term, Particle& particle)
{
	particle.weight = 1;
    double x = particle.x;
    double y = particle.y;
    double theta = particle.theta;
    std::vector predictes;
    observations = observationtoMap(observations,x,y,theta);
    landmarkinrange(predictes, sensor_range, map_landmarks, particle);
    dataAssociation(predictes, observations);
    for (int k = 0; k < observations.size(); k++) {
        double x_m = observations[k].x;
        double y_m = observations[k].y;
        double id = observations[k].id;
        double x_l = map_landmarks.landmark_list[id].x_f;
        double y_l = map_landmarks.landmark_list[id].y_f;
        
        
	    double x_term = pow(x_l - x_m, 2) / sigma_x_2sq;
	    double y_term = pow(y_l - y_m, 2) / sigma_y_2sq;
	    double pow_term = -(x_term + y_term);
        particle.weight*=outer_term*exp(-((pow((x_l-x_m),2)/sigma_x_2sq)+(pow(y_l-y_m,2)/sigma_y_2sq)));
    }
    double sum = 0;
    for (int i = 0; i < weights.size(); i++)
    	sum+=weights[i];
    for (int i = 0; i < weights.size(); i++)
    	weights[i] = weights[i]/sum;
	return particle.weight;
}
void ParticleFilter::dataAssociation(std::vector predicted, std::vector &observations) {
	double min_dist = 100000;
    double dist1 = 0;
    for ( int j = 0; j < observations.size(); j++) {
        min_dist = 100000;
        for ( int i = 0; i < predicted.size(); i++) {
            dist1 = dist(predicted[i].x, predicted[i].y, observations[j].x,observations[j].y);
            if (min_dist > dist1&&dist1<=1.0) {
                min_dist = dist1;
                observations[j].id = predicted[i].id;
                break;
            }
        }
    }
    return ;
}
void ParticleFilter::updateWeights(double sensor_range, double std_landmark[],
                                   vector &observations, const Map &map_landmarks)
{
	auto sigma_x = std_landmark[0];
	auto sigma_y = std_landmark[1];
	auto sigma_x_2sq = 2 * sigma_x * sigma_x;
	auto sigma_y_2sq = 2 * sigma_y * sigma_y;
	auto outer_term = 1 / (2 * M_PI * sigma_x * sigma_y);

	weights.clear();
	for (int i = 0, m = particles.size(); i < m; i++)
        weights.push_back(CalculateParticleWeight(sensor_range, observations, map_landmarks, sigma_x_2sq, sigma_y_2sq,outer_term, particles[i]));
    return;
}

重采样

通过为每个粒子分配权重我们知道有的粒子更可能接近真实的车辆位置，但是由于预测和更新都存在一定误差，我们也不想直接去掉权重小的粒子，于是使用了一中根据权重大小的分布来选中重采样粒子的方法。我们将所有粒子组成一个饼状图，权重越大，其所占饼的面积就越大，然后在以某一步幅在饼状图上循环采样，落在哪个权重区间就将其代表的粒子作为重采样粒子。这样权重最大的粒子就可能多次被选中作为重采样粒子。由于预测会引入高斯噪声，所以这些重采样粒子又会在该粒子周围呈高斯分布。

通过以上步骤循环滤波，最终越接近真实位置的粒子分布越密集，从而有效定位出车辆位置。重采样代码如下：

void ParticleFilter::resample() {
    discrete_distribution<> distribution(weights.begin(),weights.end());
    std::random_device rd;  //Will be used to obtain a seed for the random number engine
    std::mt19937 gen(rd());
    std::vector particles_temp;
    int index = (int)distribution(gen);
    double bate = 0.0;
    double mw = 0;
    for (int i = 0; i < weights.size(); i++)
        if(mw < weights[i])
            mw = weights[i];
    for(int i = 0; i < num_particles; i++) {
       bate += (double)distribution(gen)/10.0 *2.0 * mw;
       while (bate>weights[index]){
          bate -=weights[index];
          index = (index+1) % num_particles;
       }
       particles_temp.push_back(particles[index]);
    }
    particles.clear();
    for( int i = 0; i< num_particles; i++) {
        particles.push_back(particles_temp[i]);
    }
    return;
}

完整代码请戳这里。