FLUENT算例 —— Turbulent Pipe Flow (LES) 圆管湍流流动（大涡模拟）

来自https://confluence.cornell.edu/pages/viewpage.action?pageId=191794314
将原本的非结构网格转化成了结构网格，同时添加了关于LES相关设置的说明。

Turbulent Pipe Flow (LES) 圆管湍流流动（大涡模拟）

以ANSYS 17.0为例

问题描述

考虑通过圆形截面直管道的流动问题，圆管直径$D=0.0127m$，长度$L=5D=0.0635m$。管道进口处的平均流速为$U_{bulk}=6.58m/s$，假设流体密度为定值，$\rho =1.331kg/m^3$，流体动力粘性系数$\mu =2.34\times 10^{-5}kg/(m\cdot s)$。那么基于圆管直径、平均流速、流体密度、动力粘性系数算得该问题的Reynold数（Re）为

$$Re=\frac{\rho U_{bulk}D}{\mu }=\frac{1.331\ast 6.58\ast 0.0127}{2.34\times 10^{-5}}\approx 4750$$

接下来咱们用ANSYS FLUENT中的LES方法来求解该流动问题，绘制在距离进口$x/D$处下游截面上随着半径变化的平均速度和均方根速度，并比较由LES方法和$k-ϵ$方法模拟得到的平均速度。

1 预分析和准备工作

预分析

在大涡模拟中，瞬时速度$U(x,t)$被分解为滤波后的分量$\bar{U}(x,t)$以及剩余的残差分量$U^{\prime }(x,t)$，滤波后的速度分量表征了大尺度的非定常运动。在LES中，大尺度的湍流运动被直接表征，而小尺度的湍流运动则用模型近似。关于滤波速度的滤波方程可以从Navier-Stokes方程推出，由于残差操作，动量方程中的非线性对流项引入了一个应力张量的残差项，该残差应力张量需要通过构造模型来完成方程组的封闭，而FLUENT中提供了从易到难的多种模型。

既然咱们要求解$\bar{U}(x,t)$，那么LES就是个非定常的模拟过程，需要在时域内向前推进。为了收集统计平均量，比如平均和均方根（root mean square（r.m.s.））速度，咱们需要首先达到统计上的稳定状态（然后再开展统计平均的处理）。作为对比，$k-ϵ$模型求得的平均速度也一并给出。

关于LES的详细理论和方程可以再很多湍流的书籍中找到。

准备工作

LES是三维非定常计算（只能适用于三维问题和非定常问题），那么计算域是全部的管道。

在打开ANSYS之前，先创建一个文件夹turbulent_pipe_LES，然后里面在创建一个ICEM文件夹和FLUENT文件夹，分别用来存放ICEM的建模和画网格文件，以及FLUENT的计算文件。

2 构建几何模型

打开ICEM CFD 17.0软件，在其中完成建模工作，咱们计算域是圆管内部流道，也就是一个圆柱体，让圆柱体的轴线沿着$x$方向，进口截面位于$yOz平面$上，圆心位于坐标原点$O$。

注意：在建模过程中所用长度单位为m。

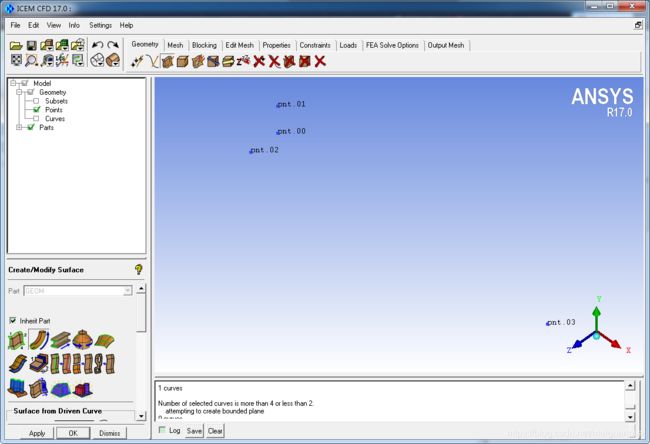
创建点

Geometry -> Create Point -> Explicit Coordinates
依次创建坐标$(x,y,z)$为$(0,0,0)$、$(0,0.00635,0)$、$(0,0,0.00635)$、$(0.0635,0,0)$的点0、1、2、3。

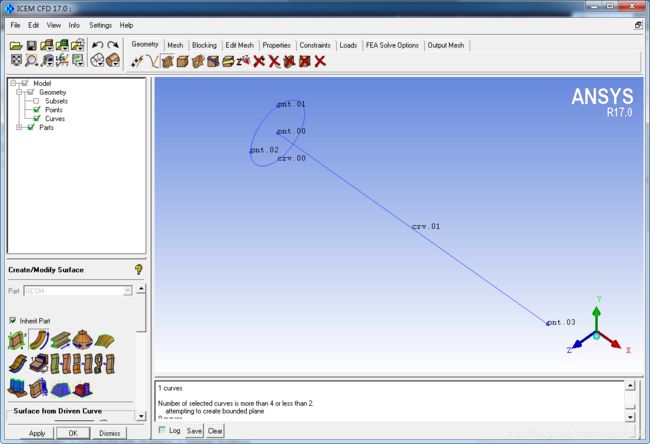
创建线

Geometry -> Create/Modify Curve -> Cricle or arc from Center point and 2 points on plane. Optional Radius
依次选中前3个点，即圆心、圆环上两个点，OK，生成进口圆环曲线crv.00

Geometry -> Create/Modify Curve -> From Points
选中第1和第4个点，即轴线上两个点，OK，生成轴线crv.01

创建面

Geometry -> Create/Modify Surface -> Simple Surface
将Simple Surface Method中由默认的From 2-4 Curves改为From Curves
选中进口的圆环，OK，生成进口面Suf.00

Geometry -> Create/Modify Surface -> Curve Driven
选择Driving Cruve为crv.01，Driven Curves为crv.00，OK，生成环面即为圆管的壁面Suf.01。

Geometry -> Create/Modify Surface -> Simple Surface
将Simple Surface Method中由默认的From 2-4 Curves改为From Curves
选中出口的圆环，OK，生成进口面Suf.02

创建体

Geometry -> Create Body -> Material Point
选中pnt.03和pnt.01两个点，则创建好了圆柱体Body

创建边界面

Parts 右击 Create Part，Part中命名为inlet，选中进口面，OK；
同样，将出口面命名为outlet；将侧面命名为pipeWall。

删除模型创建过程中多余的点、线

Geometry -> Delete Point，按下键盘中的A删除所有的点；
Geometry -> Delete Curve，按下键盘中的A删除所有的线；
Model -> Parts -> GEOM右击，Delete，删除没有几何元素的空Part。

现在就只剩下来了一个三维实体BODY，还有三个边界面INLET、OUTLET和PIPEWALL。

创建几何模型的拓扑结构

Geometry -> Repair Geometry，保持默认，Apply，再次生成表征几何体所必须的Point和Curve。
系统会根据体和面生成所必须的点和线。

之所以这么做，是为了保证体、面与点、线的关联性，便于后续网格剖分。

3 剖分网格

还是在ICEM软件中操作，接下来剖分几何体为分区结构化网格。
为确保完全，先保存下，Save Project到咱们最早新建的文件夹…\turbulent_pipe_LES\ICEM中，名字叫Pipe就好了。

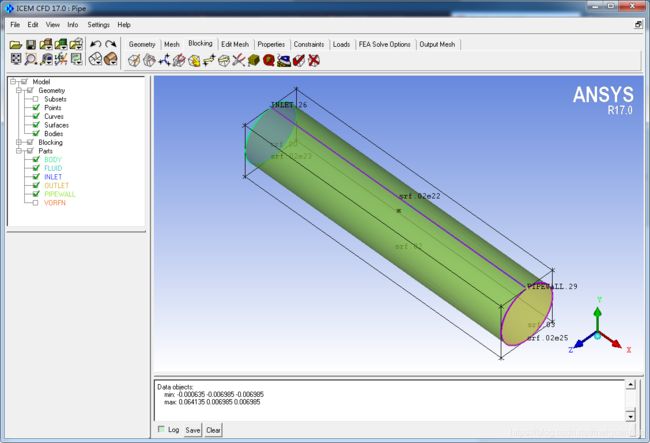
创建整体Block

Blocking -> Create Block，
Part命名为Fluid，保持默认的Initialize Blocks，选择默认的Type为3D Bounding Box，OK。

创建O-Block

Blocking -> Split Block，
选择Ogrid Block，
Select Block(s)，选择需要划分的Block；
Select Face(s)，选择进口与出口的两个面；
OK，即可看到切分好的O-型分区。

建立映射关系

Blocking -> Associate -> Snap Project Vertices，选择All Visible，OK。
则Block中的点自动和几何体中最近的点映射到一起了。

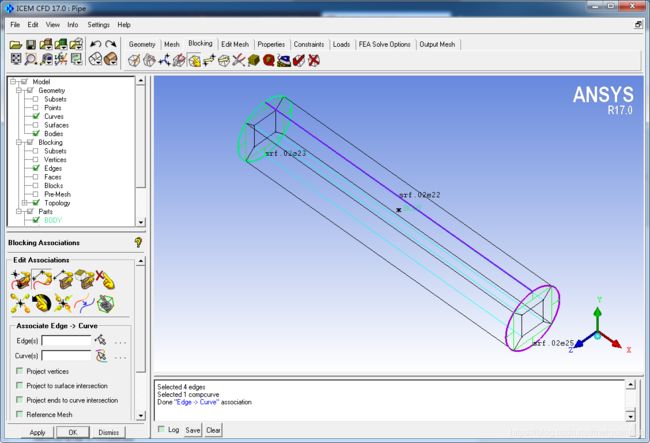
Blocking -> Associate -> Associate Edge to Curves -> Associate Edge to Curves，
将对应的Block中的Edge映射到几何体的Curves上。

定义网格节点数目

Blocking -> Pre-Mesh Params -> Edge Params

将所有轴向Edge设置为均分160个单元，这样单元尺度为$h=0.0635m/160\approx 4\times 10^{-4}m$；
将进出口处与1/4圆弧对应的Edge均分为25个单元，这样单元尺度为$h=0.0127m\ast \pi /4/25\approx 4\times 10^{-4}m$；
将壁面边界层网格，即O-结构网格的四个径向Edge设置为首层网格$h_0=5\times 10^{-6}m$，等比增长比例为1.1，总共40层网格。

生成网格

Model -> Blocking -> Pre-mesh，Yes。
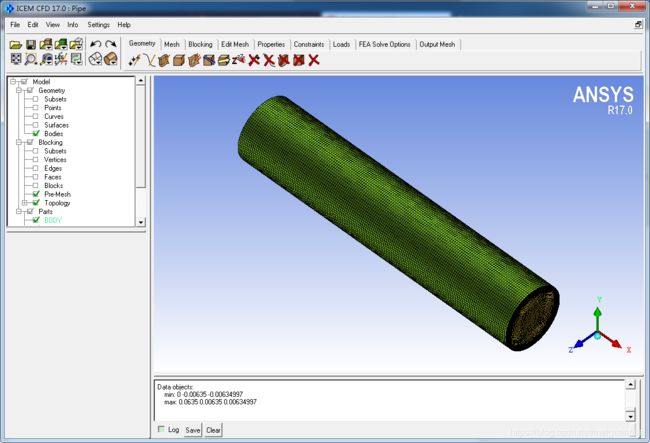
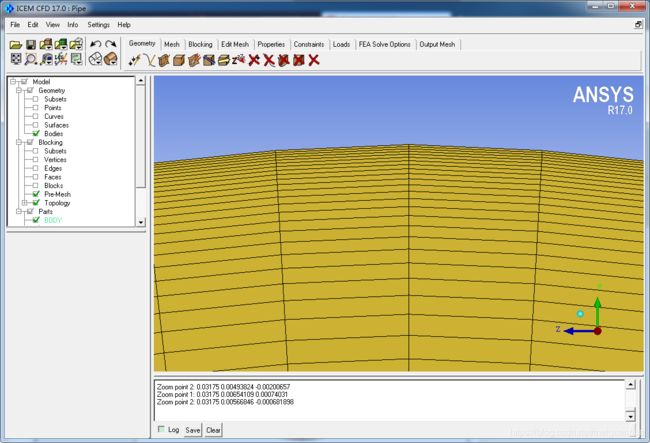Model -> Blocking -> Pre-mesh右击Pre-Mesh Info，可看网格信息：

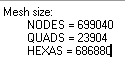
其节点总数约70万，其六面体单元总数约70万。

检查网格质量

Blocking -> Pre-Mesh Quality Histograms，
选择Criterion为Determinant 2x2x2，Apply。

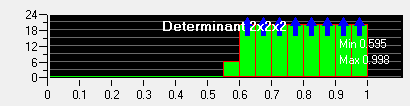
选择Criterion为Angle，Apply。

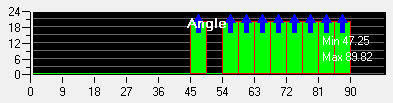
网格质量还好的，可以导出网格做计算了。

导出网格文件

Model -> Blocking -> Pre-Mesh，右击，选择Convert to Unstruct Mesh，
信息框出现“Current Coordinate system is global”，则表示转化完成。
File -> Mesh -> Save Mesh As，保存当前网格文件为Pipe_Str.uns。

Output Mesh -> Select solver，
保持Output Solver为默认的ANSYS Fluent，Apply。

Output Mesh -> Write input，
Yes保存现有Project，在跳出的窗口中选择刚才保存的网格文件Pipe_Str.uns，
在随后弹出的窗口中选择3D，可将Output file名字改为Pipe_Str，Done完成输出。

关闭ICEM软件。

4 物理问题设置（Setup设置）

接下来需要在FLUENT当中进行CFD设置和计算了。

打开FLUENT软件：
咱们求解的是三维问题，当然设置成3D了；
为了提高精度，一般都是用的Double Precision双精度模式，因为默认的单精度real计算误差太大了，没谁会拿它来跑计算的；
Precessing Options下，打开Parallel并行计算，然后把Processes中设置成你想用的CPU核数，由于LES是非定常和三维的运算，其计算量非常大，如果用Serial串行计算，那么可能要耗费数月的时间才能算好，所以条件允许的话，尽可能用多核并行计算吧，不然你要等到黄花菜都凉了。。。

读入/检查/缩放网格

File -> Read -> Mesh，找到刚才咱们输出的Pipe_Str.msh文件，把它读进来。

Setting Up Domain -> Info -> Size，查看下网格单元、面、节点数目。

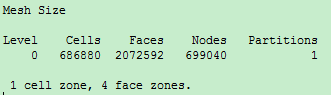
Setting Up Domain -> Display，显示网格。
Setting Up Domain -> Check，检查网格，注意看又没有负体积，计算域的x、y、z上下限是不是跟之前建模的一样，如果不一致，是不是差了一定倍数，那就需要做Scale缩放处理。这里一切都OK的，表明网格没问题。

通有设置

Setup -> General，保持默认Pressure-Based Solver，压力基求解器适用于不可压缩流动，将Time下的默认Steady改为Transient，因为LES只能是非定常三维计算。

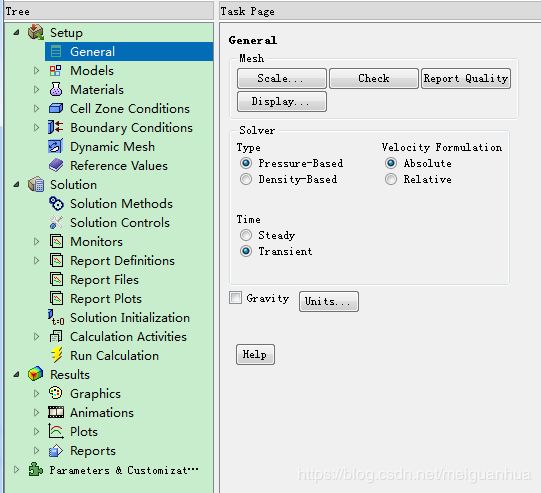
模型设置

Setup -> Models -> Viscous - Laminar，Edit…，Model选择Large Eddy Simulation (LES)，Subgrid-Scale Model选择WMLES，这个模型对网格的要求最低（可查看FLUENT帮助文档里的详细说明），OK。
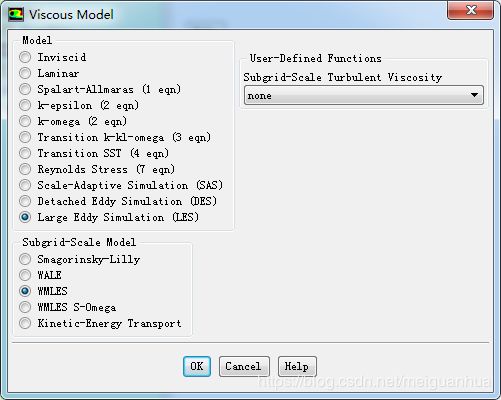跳出来个信息框，其实是告诉你，要是用LES的话，空间离散和时间离散都要求比较高，必须要用到它推荐的这些离散格式。即，空间用有界中心差分，时间用有界二阶隐式格式。当然，系统已经自动帮你设置好了。OK关掉它就好了。

物性参数

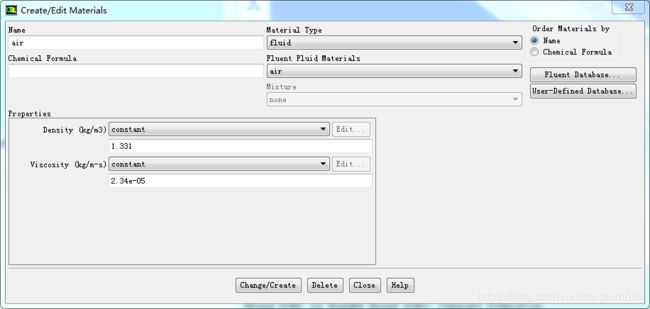
Setup > Materials > Fluid > Create/Edit… ，
在打开的窗口中，设置密度$\rho =1.331kg/m^3$，流体动力粘性系数$\mu =2.34\times 10^{-5}kg/(m\cdot s)$，Change/Create，Close。

边界条件

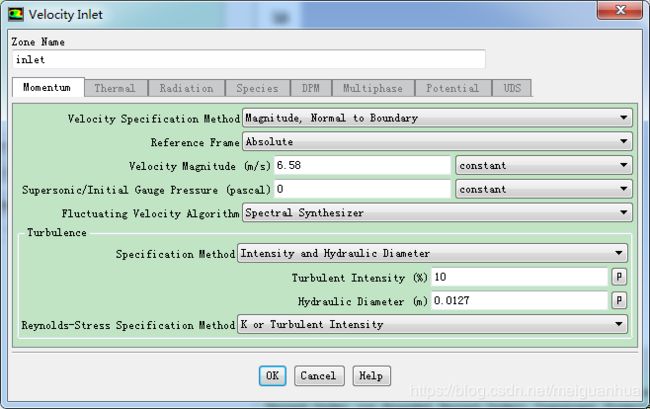
Setup > Boundary Conditions > inlet，确认其类型是velocity-inlet，Edit…，

设置Velocity Specification Method为Magnitude, Normal to Boundary：
设置Velocity Magnitude (m/s)为6.58 m/s，
设置Fluctuation Velocity Algorithm为Spectral Synthesizer （SS方法，在进口处生成扰动的湍流速度分布，而非均匀恒定的速度场）；

设置Turbulence Specification Method为Intensity and Hydraulic Diameter，用强度和水力直径设置湍流：
设置Turbulent Intensity (%)为10 %，湍流强度10%，
设置Hydraulic Diameter (m)为0.0127 m，水力直径用圆管直径给定即可；

设置Reynolds-Stress Specification Method为K or Turbulent Intensity。

OK关闭进口速度设置对话框。

确保outlet边界类型为Pressure-outlet，并保持默认设置即可。

确保pipewall边界类型为wall，并保持默认设置即可。

确保int_fluid边界类型为interior，这个实际上是计算域内部的面。

设置参考值

Setup > Reference Values，选择Compute from为inlet，即可。

至此，物理问题描述完毕，可以选择保存下文件到先前的文件夹…\turbulent_pipe_LES\FLUENT：
File -> Write -> Case，将Case命名为Pipe即可，OK。

5 求解器设置（Solution设置和求解）

求解方法

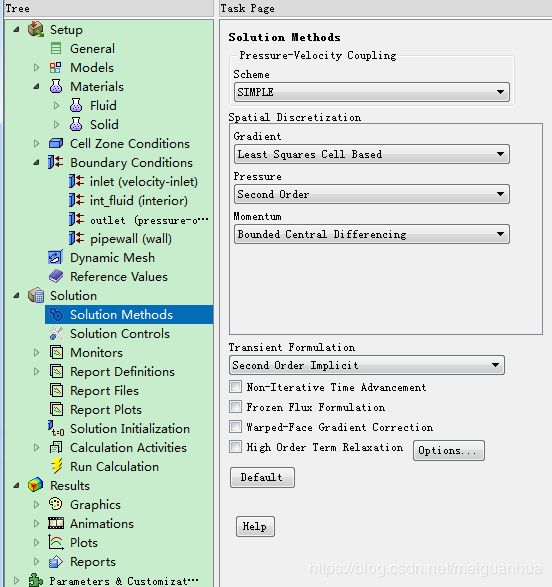
Solution -> Solution Methods，
设置Scheme为默认的SIMPLE，
设置Momentum为默认的Bounded Central Differencing，（还记得前面选择LES模型时的提示么）
设置Pressure为Second order，
设置Transient为Second Order Implicit。

初始流场设置

Solution -> Solution Initialization， 选择Compute from为inlet，然后点击initialize来完成初始化流场。

设置收敛标准

Solution -> Monitors > Residuals - Print, Plot，Edit…，
将连续方程和x、y、z速度的收敛指标全部设置为1e-6，OK。

开始计算

先算到统计稳态状态

Solution -> Run Calculation，
设置Time Step Size(s)为1e-05，
设置Number of Time Steps为10000，
勾选Extrapolate Variables选项，
设置Max Iterations/Time Step为默认的20次。

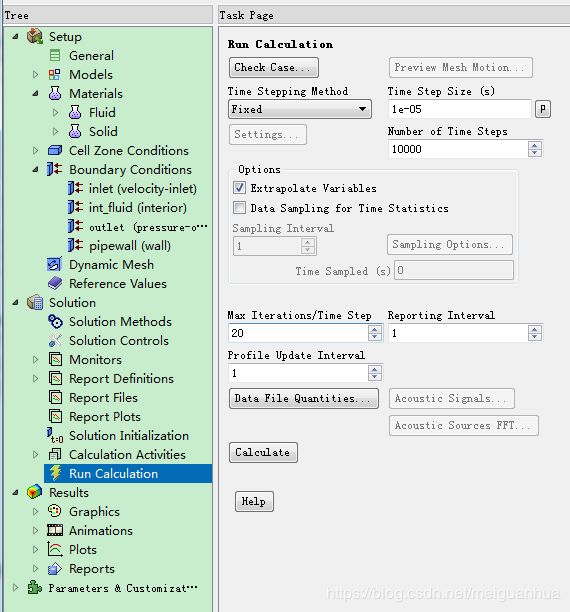
为确保万全，先保存下case和dat，然后点Calculate开始计算，愉快地出现了残差收敛曲线，虽然刚开始20步不足以收敛到1e-6，但没过几部之后，系统就不需要20步就能收敛到1e-6了，所以计算精度还是OK的。

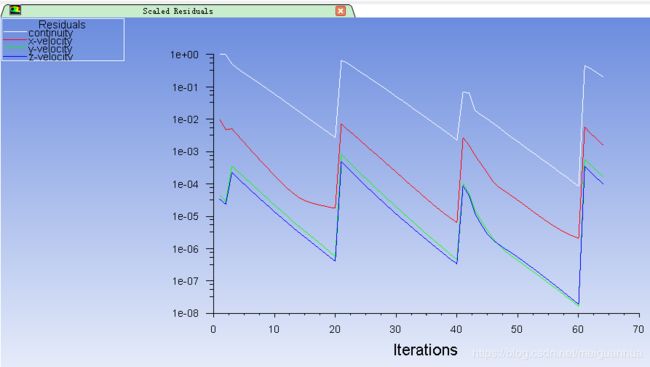
注意：这里的10000步算到0.1s，这样的计算值仅仅是为了让流场发展到统计稳定状态（也就是类似于振动力学里面的稳态响应状态），然后再从0.1s开始后续的10000步计算到0.2s，边算边统计，以获取0.1-0.2s的统计平均值。

由于我电脑比较烂，所以用的是单核串行计算……只能苦苦等待了……

经过多天等待，终于算完了前10000步的0-0.1s，那么接下来就要再次计算10000步从0.1-0.2s，并且再算的过程中开启统计功能。

再次计算前，可以看下中面上美丽的瞬态速度场、涡量场、压力场的云图，这些细碎凌乱、看似毫无规律、细思又隐含若干规则的结构，恰是湍流的瞬态特性。

速度场
涡量场

压力场

紧接着再次计算并开启统计量的计算

Solution -> Run Calculation，

设置和前面是一样的，即：设置Time Step Size(s)为1e-05，设置Number of Time Steps为10000，勾选Extrapolate Variables选项，设置Max Iterations/Time Step为默认的20次。

唯一的不同是，此时勾选Data Sampling for Time Statistics选项，来开启对时均统计量的数据采样处理工作，这样FLUENT在时域计算的同时便开始了对流场变量的时间平均计算（即统计平均量的计算），当时域计算完成后，除了能看到0.2s瞬时的物理量，还得到了0.1-0.2s的时均统计平均物理量。

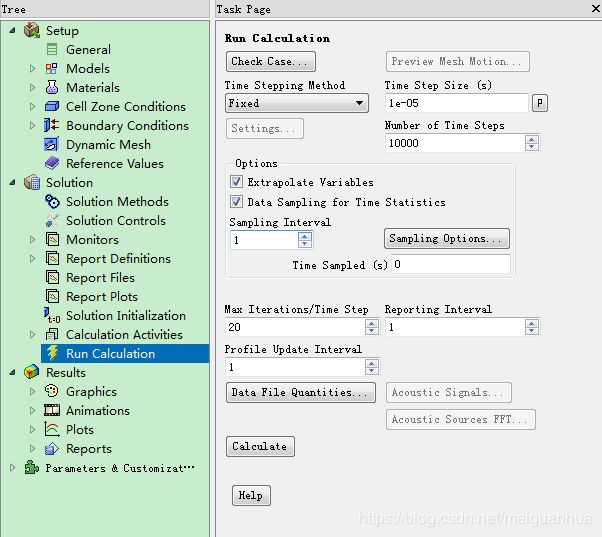
点击Calculate开始时域计算和统计量的计算，又是漫长的等待过程……

终于终于算好了，噢耶，可以后处理和结果分析了。

6 数值结果与分析

注意在LES模拟中有两种速度，瞬时速度和时均速度。瞬时速度是计算域在某个时刻的真实速度，当我们收集统计量的时候，将瞬时速度做时间平均来获取平均速度。让咱们在计算域中设置一个中面来看看在它上面的瞬时轴向速度和平均轴向速度的云图是个什么样子吧。

轴向速度云图

Results -> Graphics and Animation -> Contours -> Set Up…，
在Countours窗口，点击New Surface -> Plane…，
在Plane Surface窗口，勾选Point and Normal，输入点坐标为(x0 (m), y0 (m), z0 (m)) = (0,0,0)， 输入法向量为(ix (m), iy (m), iz (m)) = (0,0,1)，将New Surface Name命名为. Name the surface as plane-mid，点击Create完成中面创建。

可以用Graphics and Animations -> Mesh -> Set Up…，选择和查看这个创建好的面。

回到contour窗口，在Contours of中选择Velocity… 和X Velocity，在Surfaces中选择plane-mid，点击Display，下图显示出了瞬态轴向速度云图。

若想绘制平均轴向速度，则在Contours of中选择Unsteady Statistics…和Mean X Velocity，在Surfaces中选择plane-mid，点击Display，下图显示出了平均轴向速度云图。

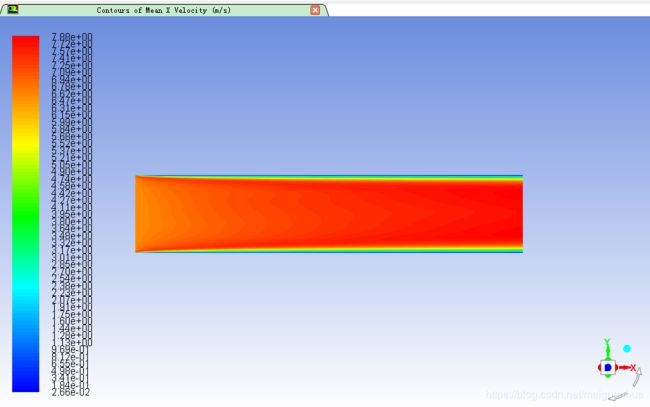
从这俩图中，可以很清晰地看出瞬态量和平均量的不同之处，平均量恰如是做了定常假设的湍流场，而瞬态量则是瞬时湍流结构的真实体现，很多细碎漂亮的小涡结构，即传说中的相干结构（拟序结构）。

轴向速度的XY图

咱们接下来整个横穿管道中心的线，来看看这根线上平均轴向速度的分布情况，并在下个小节中将结果与$k-ϵ$模型的结果作对比。

点击Plots -> XY Plot -> Set Up…，

在Solution XY Plot窗口，点击New Surface -> Line/Rake…，

在the Line/Rake Surface窗口，输入端部点坐标(x0 (m), y0 (m), z0 (m)) = (0.03175,-0.00635,0)和(x1 (m), y1 (m), z1 (m)) = (0.03175,0.00635,0)，将New Surface Name命名为line-mid，点击Create。完成中线的创建。

这根线可以在Graphics and Animations > Mesh > Set Up…中查看。

回到Solution XY Plot窗口，在Y Axis Function中选择Unsteady Statistics… 和Mean X Velocity，在Plot Direction输入(X,Y,Z) = (0,1,0)，在Surfaces下选择line-mid，点击Plot绘制平均轴向速度沿着中线的分布图。

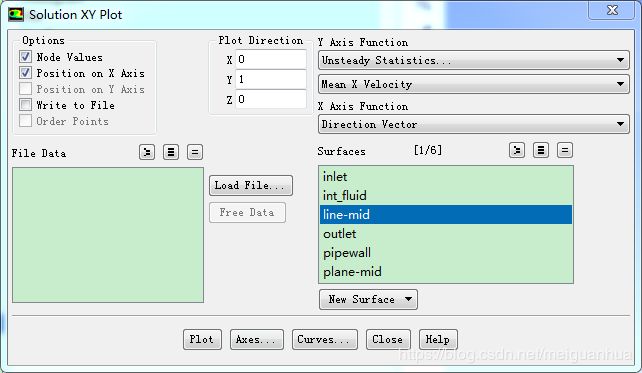
若要保存这些离散点，那么在Solution XY Plot窗口中选择Write to File，点击Write，选择位置并将其保存为MeanXVel_LES.xy文件即可。

当然，也可以查看瞬态x速度的分布情况，与平均值相比，它凌乱多了。

7 验证和确认（Verification & Validation）

用$k-ϵ$模型来计算湍流管道流动

当然要把原有的cas和dat再复制一个复件出来，然后在上面更改设置了：

Setup -> General，选择Steady定常问题，点击OK关掉跳出来的警告。它提示LES必须用非定航算，不能用定常，咱们后面把LES改成$k-ϵ$模型的。

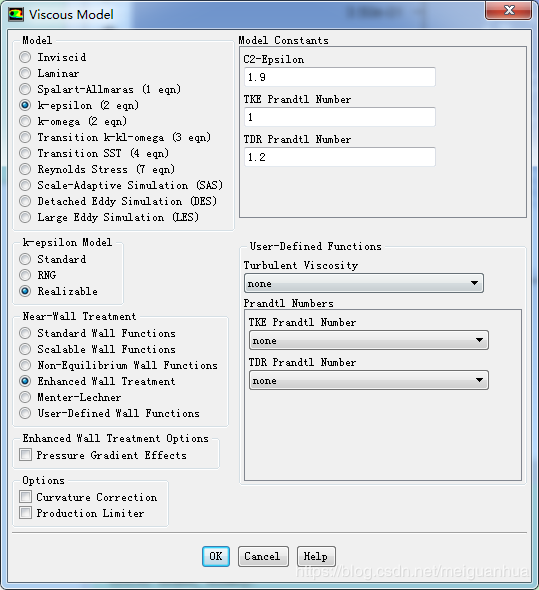
Setup -> Models -> Viscous，Edit…，

在Viscous Model窗口，Model中选择k-epsilon (2 eqn)， k-epsilon Model中选择Realizable，Near-Wall Treatment选择Enhanced Wall Treatment，点击OK确认。
因为咱们这个网格画的足够好（y+<1），所以可以用加强壁面处理方式来做近壁处理。

Setup -> Boundary Conditions，选择Outlet点击Edit…，将Turbulence Specification Method改为 Intensity and Hydraulic Diameter，将Backflow Turbulent Intensity设为10%，将Backflow Hydraulic Diameter设为0.0127m，OK确认。

接下来，Solution -> Solution Methods，对于Turbulent Kinetic Energy和Turbulent Dissipation Rate选择Second Order Upwind。

Solution -> Monitors > Residual，点击Edit…，对k和epsilon设置为1e-6。为了获得较快的收敛，将continuity设为1e-5，OK确认。

Solution -> Solution Initialization，点击Compute from选择inlet，点击initialize完成初始化。

Solutioin -> Run Calculation，将Number of Iterations设为1000，点击Calculate，开始计算。

大约600步便收敛了。

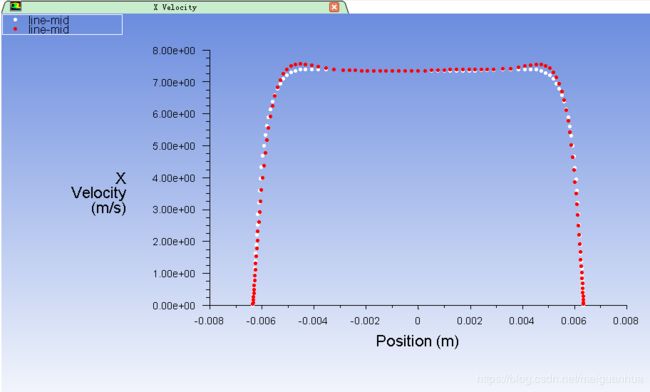
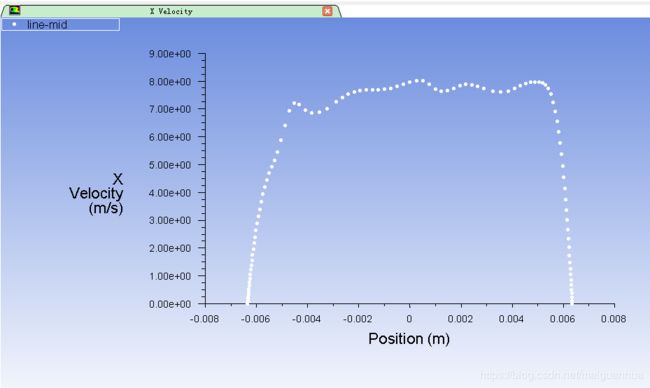
中线速度比较

算好后，绘制中线上的x-velocity，并load进之前LES算得的平均x-velocity，将两者绘制于同一个XY Plot中，白色为k-e，红色为LES的统计平均量，可见，两者吻合较好，从而验证了LES计算结果的正确性。