理解闭包的前置条件—— λ演算和作用域规则
前言
这几天用Scala写了一堆流计算程序,在翻阅Scala文档时看到了闭包一节,不知怎么就回忆起了自己上大二时用JavaScript做创新项目的经历——因为JS闭包的原理对当时的我来说很费解,以至于熬了一整个通宵才差不多弄明白。正好这几天博客素材有点缺乏,那么就总结一下“闭包”这个神叨叨的词背后的东西吧。
实际上,闭包的概念同时存在于离散数学和计算机科学的领域中,并且这两种“闭包”之间没有什么明显的关联。对程序员而言,我们接触到的闭包就是函数式编程(functional programming)情境下的一种语言特性,我主要想说的也就是这方面。当然,离散数学那边的事情也会抽空聊两句。
要想真正地搞懂闭包,我们就必须追根溯源。所以本文暂时不会请出本尊,而是介绍两个必备的前置知识:一为λ演算,二为作用域规则。
λ演算与函数式编程
λ演算(lambda calculus)是所有函数式编程语言的基础,而闭包又与函数式编程强相关,故有必要最先说说λ演算。
非正式地来讲,λ演算是一种“一元函数生万物”的演算规则,早在上世纪30年代由美国数学家阿隆佐·邱奇(Alonzo Church)提出。一言以蔽之,λ演算将我们正常理解的计算过程抽象为单变量(标量)及一元函数的定义和应用过程。这句话并不容易理解,下面举个栗子。
假设我们有个最简单的函数f(x) = x + 2,用λ演算来表示,如下:
λx.x + 2 (参数名x可以随意写)
用λ演算表示f(7) = 7 + 2 = 9的过程,如下:
(λx.x + 2) 7 = 7 + 2 = 9
如果是像g(x, y) = x - y这样的二元函数,该怎么办呢?答案是用高阶一元函数。简单说来就是拆成两个一元函数来表示,其中一个函数返回值是函数,如下:
λx.(λy.x - y) (λ演算是左结合的,所以这里括号删掉不会有歧义)
这其实就是之前曾简单谈过的函数柯里化(currying)思想。用λ演算表示g(7, 2) = 7 - 2 = 5的过程,如下:
(λx.λy.x - y) 7 2 = (λy.7 - y) 2 = 7 - 2 = 5
由此可见,λ演算实际上就是反复的函数求值过程。并且它的基本规则很简单,只有三种:
- x,定义变量标识符;
- λx.M,通过表达式M定义一元函数,其参数为x。此时就说变量x在表达式M中被约束(bound);
- M N,将表达式N作为参数应用到表达式M定义的函数上,也就是平时说的代入求值。
所以,λ演算的规则可以用上下文无关文法(即乔姆斯基分类中的2型文法)表示,以下是BNF范式的描述,也是相当容易:
<表达式> ::= <标识符>
<表达式> ::= (λ<标识符>.<表达式>)
<表达式> ::= (<表达式> <表达式>)
其中标识符从预先设定好的标识符集合中取得。括号用来表达运算优先级,在没有歧义的情况下可以去掉(比如上文的λx.λy.x - y)。
通过了解λ演算,看官要特别注意以下三个特征:
- 函数可以赋值给标识符(变量);
- 函数可以作为函数的参数进行传递;
- 函数的结果(返回值)可以是函数。
函数式编程语言(如JS、Scala)全部具有这三个从λ演算继承而来的特征,亦即函数是名正言顺的一类对象(first-class object),也称作“一等公民”(first-class citizen),与最常见的int、long等最原始的值类型享有相同的地位。相反地,我们熟识的以C系语言为代表的指令式(imperative)编程语言就不具备这些特点。
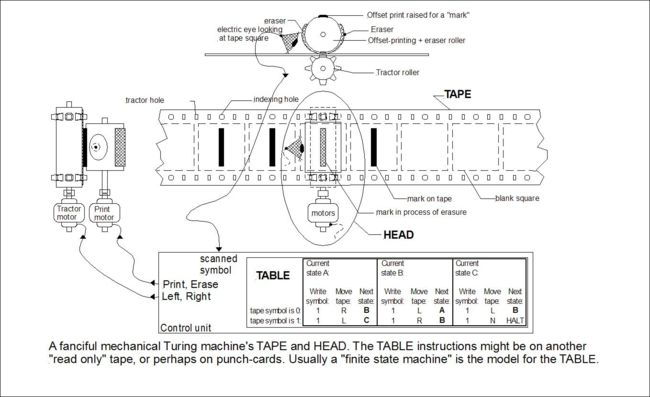
为什么要煞费苦心地搞出λ演算这么一套复杂的规则呢?因为邱奇与和他同时代的学者们希望发明一种通用的计算模型,通过它能够计算(当时的)任意表达式的结果。读了这句话,看官可能会想起图灵和他的图灵机。没错,图灵机和λ演算(以及前后出现的其他通用计算模型)都是计算机科学的起源,并且它们的计算能力是等价的。现代编程语言都是图灵完全的,而在λ演算的基础上,才产生了函数式编程,意义很重大。
下图示出一种机械式图灵机的构造。
下表则是邱奇本人发明的“邱奇数”(Church numeral)的λ演算定义及基础运算规则。
由此可见,自然数n其实就是将函数f应用n次的高阶函数,说明λ演算确实是一种有效的计算模型。为了避免陷入太多细节跳不出来,如果想看更多的内容(比如邱奇数是否可以表示负数),还请参见上面的传送门。
编程语言的作用域规则
作用域
通俗来讲,作用域(scope)就是指程序源码中标识符的定义有效的那部分区域。平时我们在说“全局变量”、“本地变量”这些词时,其实都是在描述它们的作用域,即在全局有效、在本地有效。当然,能够用标识符代表的东西不止变量,还有类、命名空间、函数、方法等等等等。但是在本文中,为了不致使问题复杂化,我们只关心变量和函数的作用域。
下面用JavaScript举个例子(因为它语法比Scala简单得多),图中每个不同颜色的框就代表一个作用域。
理解了作用域,那么一门编程语言的作用域规则自然就是确定标识符作用域的法则。目前只有两种作用域规则,分别来看看。
词法作用域规则
考虑以下JS代码。
var p = 1;
function f() {
console.log("p in f(): " + p);
p = 2;
}
function g() {
var p = 3;
f();
console.log("p in g(): " + p);
}
g();
console.log("p: " + p);
执行结果如下。
> "p in f(): 1"
> "p in g(): 3"
> "p: 2"
该结果显然是符合“常理”的。这是因为包括JS在内的绝大多数语言都遵循词法作用域规则(lexical scoping)。
以上面代码为例,函数g()执行时,会调用函数f()。虽然f()在g()的作用域内被调用,但是它的执行不会受到g()作用域环境的影响,所以f()向上在全局作用域内找到初值为1的变量p,并执行赋值为2的操作。而g()在执行时,首先找到的是自己作用域内定义的那个p,所以最终输出是3。
也就是说,在词法作用域规则下,作用域是严格按照标识符(函数)的定义来的——因为f()和g()一样被定义在全局作用域内,所以f()并不是g()的一部分。只有当f()嵌套定义在g()内部时,才能视为g()的一部分。标识符的定义就是代码,从代码能直观地看出作用域的范围,这就是lexical一词的由来。另外,作用域在代码编译期就可以确定不变,故词法作用域规则又叫静态作用域规则(static scoping)。
动态作用域规则
将上一小节的JS代码改写为Shell,如下。
p=1
function f() {
echo "p in f(): $p";
p=2;
}
function g() {
local p=3;
f;
echo "p in g(): $p";
}
g
echo "p: $p"
执行结果如下。
p in f(): 3
p in g(): 2
p: 1
神奇了,为什么会是3、2、1?
这是因为以Shell为代表的一小撮语言采用的是动态作用域规则(dynamic scoping)。与词法作用域规则相反,动态作用域规则按照标识符(函数)的调用来区分作用域。函数f()在g()内部被调用时,它就受到了g()作用域的影响,看到的变量p不再是全局作用域内的变量p,而是g()内定义的那个,全局的p最终没有被操作。也就是说,动态作用域是在程序运行期确定的,代码本身可能无法反映出正确的作用域。
动态作用域规则并不是重点。在后文探索闭包的过程中,我们就会理解它与λ演算和词法作用域规则之间的关系了。
To be continued
为了让自己能够善始善终,以及留个小悬念,最后引入一个经典的关于闭包与对象的故事。Scheme语言大佬Anton van Straaten在这里写道:
The venerable master Qc Na was walking with his student, Anton. Hoping to
prompt the master into a discussion, Anton said "Master, I have heard that
objects are a very good thing - is this true?" Qc Na looked pityingly at
his student and replied, "Foolish pupil - objects are merely a poor man's
closures."
Chastised, Anton took his leave from his master and returned to his cell,
intent on studying closures. He carefully read the entire "Lambda: The
Ultimate..." series of papers and its cousins, and implemented a small
Scheme interpreter with a closure-based object system. He learned much, and
looked forward to informing his master of his progress.
On his next walk with Qc Na, Anton attempted to impress his master by
saying "Master, I have diligently studied the matter, and now understand
that objects are truly a poor man's closures." Qc Na responded by hitting
Anton with his stick, saying "When will you learn? Closures are a poor man's
object." At that moment, Anton became enlightened.
“对象是穷人的闭包”、“闭包是穷人的对象”,这两句看似对立的话实际上都是正确的。只有合二为一,才能说真正理解了它们之间的异同。Anton本人也认为,对象与闭包的问题是非常有禅意(koan)在其中的。欲知后事如何,且听下回分解吧。
晚安。