数字图像处理（五）：频域滤波

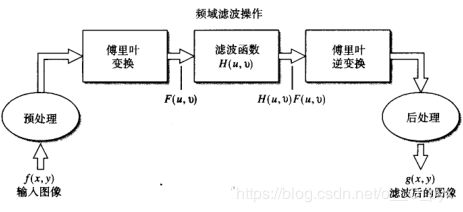
1 基本概念

你要是问傅里叶变换，请看这里

1.1 卷积定理

1.2 折叠误差

若使用DFT进行滤波操作，且周期关于函数的非零部分持续时间很靠近，相邻周期会产生干扰。
措施

函数paddedsize

用于计算满足前述等式的P和Q的最小偶数值。

1.3 快速DFT步骤

假设滤波函数H(u, v)的大小与填充后的图像大小相等

PQ = paddedsize（size（f））；%使用paddedsize获得填充参数；如果输入是彩色图像，必须要灰度化rgb2gray
F = fft2(f, PQ(1), PQ(2));%得到使用填充的傅里叶变化
%生成一个大小为PQ(1)  X  PQ(2) 的滤波函数H。如果该滤波函数已居中，使用前要令H = fftshift(H)
G = H.*F;%将变换乘以滤波函数
g = real(ifft2(G));%获得G的傅里叶逆变换的实部
g = g(1:size(f,1), 1:size(f, 2));%将左上部分的矩形剪切为原来尺寸大小

1.4 有限冲击响应（FIR）滤波器

若线性系统只是一个空间滤波器，通过简单地观察它对冲击的响应，就可以完全地确定该滤波器。

1.5 用于频域滤波的M函数

函数dffilt

function g = dffilt(f, H)
F = fft2(f, size(H, 1), size(H, 2)); %得到使用填充的傅里叶变化
g = real(ifft2(H.*F));%滤波处理
g = g(1:size(f, 1), 1:size(f, 2));%剪裁图像至原始尺寸

2 生成滤波器

2.1 从空间滤波器获得频域滤波器

函数freqz2

计算FIR滤波器的频率响应。

H = freqz2(h, R, C)

h 二维空间滤波器，H 相应的二维频域滤波器，R H的行数，C H的列数。R = PQ(1), C = PQ(2)
若freqz2无输出参量，则H的绝对值会在MATLAB桌面上显示为三维透视图。

%读入图像
f = imread(filename);
%获得图像f的傅里叶频谱
F = fft2(f);
S = fftshift(log(1 + abs(F)));
S = gscale(S);
imshow(S)
%生成空间滤波器
h = fspecial('sobel')'
%查看相应频域滤波器的图形
freqz2(h) 
%滤波器本身通过如下命令获得
PQ = paddedsize(size(f));
H = freqz2(h, PQ(1), PQ(2));
H1 = ifftshift(H);
%显示H和H1的绝对值
imshow(abs(H), [])
figure, imshow(abs(H1), [])

%在空间域中滤波后图像
%该语句默认用0填充边界。
gs = imfilter(double(f), h);
%频域滤波后图像
gf = dftfilt(f, H1);

imshow(gs, [])
figure, imshow(gf, [])

%灰色调是由于gs和gf存在负值，会使图像的平均值在使用imshow后增大
figure, imshow(abs(gs), [])
figure, imshow(abs(gf), [])
%创建一幅阈值二值图像
figure, imshow(abs(gs > 0.2*abs(max(gs(:)))))%仅显示强度比gs最大值的20%还要大的边缘
figure, imshow(abs(gf > 0.2*abs(max(gf(:)))))

d = abs(gs - gf);
max(d(:))
min(d(:))%通过计算最大差和最小差说明
%空间滤波和频域滤波得到的图像相同

2.2 从频域直接生成滤波器

函数dftuv

dftuv能够得到一个网格数组,利用网格数组能够得到任何一点到频率矩形中指定点的距离。

function [U,V]=dftuv(M,N)
u=single(0:(M-1));
v=single(0:(N-1));
idx=find(u>M/2);
u(idx)=u(idx)-M;
idy=find(v>N/2);
v(idy)=v(idy)-N;
[V,U]=meshgrid(v,u);

利用生成的网格数组能够得到任何一点到频率矩形中指定点的距离。
将 DSQ的ans进行fftshift（将零频分量移到频谱中心）后得到的就是各点相对频域中心点的距离的平方，如下

[U,V]=dftuv(8,5);
>> DSQ=U.^2+V.^2

DSQ =

  8×5 single 矩阵

     0     1     4     4     1
     1     2     5     5     2
     4     5     8     8     5
     9    10    13    13    10
    16    17    20    20    17
     9    10    13    13    10
     4     5     8     8     5
     1     2     5     5     2

>> fftshift(DSQ)

ans =

  8×5 single 矩阵

    20    17    16    17    20
    13    10     9    10    13
     8     5     4     5     8
     5     2     1     2     5
     4     1     0     1     4
     5     2     1     2     5
     8     5     4     5     8
    13    10     9    10    13

2.3 低通频域滤波器

**理想低通滤波器（ILPF）**的传递函数：

其中D0是正数，D(u,v)是点（u,v）到滤波器中心的距离。该滤波器乘以一幅图像的傅里叶变换，显然滤波器会切断以D0为半径的圆的圆外F(u,v)分量，圆内以及圆上保持不变。但是事实上电子元件无法实现理想的低通滤波器。
常用的有，巴特沃斯低通滤波器，高斯低通滤波器等。
**n阶巴特沃斯低通滤波器（BLPF）**的传递函数是：

在滤波器中心D0有截止频率，与理想滤波器的区别在于在D0出没有一个尖锐的不连接点。当D(u, v) = D0时，H(u, v) = 0.5
**高斯滤波器（GLPF）**的传递函数:

当D(u, v) = D0时，H(u, v) = 0.607

函数lpfilter

定义M函数生成低通滤波器的传递函数

function H=lpfilter(type,M,N,D0,n)
%LPFILTER Computes frequency domain lowpass filter
[U,V]=dftuv(M,N);
D=hypot(U,V);
switch type
    case 'ideal'
        H=single(D<=D0);
    case 'btw'
        if nargin==4
            n=1;
        end
        H=1./(1+(D./D0).^(2*n));
    case 'gaussian'
        H=exp(-(D.^2)./(2*(D0^2)));
    otherwise
        error('unkonw filter type.')
end

2.4 三维线框图和表面图

函数 mesh

绘制线框图的最简单方法是使用函数 mesh：mesh(H)
该函数将绘制一个 x = 1:M 和 y = 1:N 的线框图，其中 [M,N] = size(H)
若 M 和 N 很大，可以使用语法每隔 k 个点绘制：mesh(H(1:k:end,1:k:end))
通常，沿每个轴 40 到 60 个细分，外观和分辨率会得到较好的平衡
函数 mesh 仅支持 double 类和 uint8 类，如果 H 是一个滤波器函数，为节省内存，使用语法 mesh(double(H))

MATLAB默认情况下使用彩色绘制网线，命令：colormap([0 0 0])，将线框设置为黑色

MATLAB 还会将网格和坐标轴放到网格图上，可以使用以下命令
关闭网格：grid off ； 打开网格：grid on;
关闭坐标轴：axis off 打开坐标轴：axis on

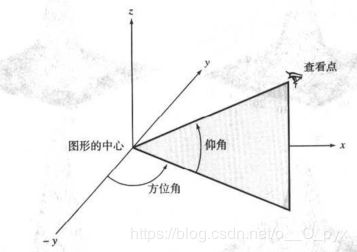
观察点(观察者的位置)由函数 view 控制：view(az,el)

% 使用高斯低通滤波器
>> H = fftshift(lpfilter('gaussian',500,500,50));
>> mesh(double(H(1:10:500,1:10:500)))
>> axis tight	% 将轴的上下限设置为数据范围
>> colormap([0 0 0])	% 将线条转换为黑色
>> axis off	% 去掉坐标轴
% 设置方位角为 -25，将仰角设置为0
>> view(-25,0)

函数surf

将函数绘制成表面图而不是线框图
该函数与函数 mesh 一样，生成相同的图形，只是网格中的四边形会被彩色填充（小面描影）。
可使用命令将彩色转换为灰度：colormap(gray)

>> H = fftshift(lpfilter('gaussian',500,500,50));
>> surf(double(H(1:10:500,1:10:500)))
>> axis tight
>> colormap(gray)
>> axis off
% 进行插值：平滑小面描影并去掉网格线
>> shading interp

双变量绘图

当目标是绘制双变量的一个解析函数时，可使用 meshgrid 生成坐标值，由这些坐标值，可生成将在 mesh 或 surf 中使用的离散矩阵。

% 在函数 meshgrid 中首先列出各列 (Y)，然后列出各行(X)
[Y,X] = meshgrid(-2:0.1:2,-2:0.1:2);
Z = X.*exp(-X.^2 - Y.^2);
mesh(Z)
figure,surf(Z)

2.5 锐化频域滤波器

函数hpfilter

function H=hpfilter(type,M,N,D0,n)
%HPFILTER Computes frequency domain highpass filters
if nargin == 4 %输入参数数目为4
    n = 1;%默认值
end
% 生成高通滤波器
Hlp = lpfilter(type, M, N, D0, n);
H = 1- Hlp;
end

2.6 高频强调滤波

a是偏移量，b是乘数，Hhp(u, v)是高通滤波器的传递函数。

PQ = paddedsize(size(f));
D0 = 0.05*PQ(1);
HBW = hpfilter('btw', PQ(1),PQ(2), D0, 2);
H = 0.5 + 2*HBW;
gbw = dftfilt(f, HBW);
gbw = gscale(gbw);
ghf = dftfilt(f, H);
ghf = gscale(ghf);
ghe = histeq(ghf, 256);