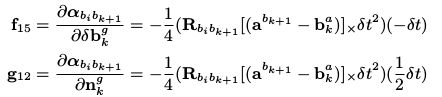手写VIO学习总结（三）

系列笔记:
手写VIO学习总结（一）
手写VIO学习总结（二）

1. 作业1

1 样例代码给出了使用LM 算法来估计曲线y = exp(ax2 + bx + c)
参数a, b, c 的完整过程。

作业1.1

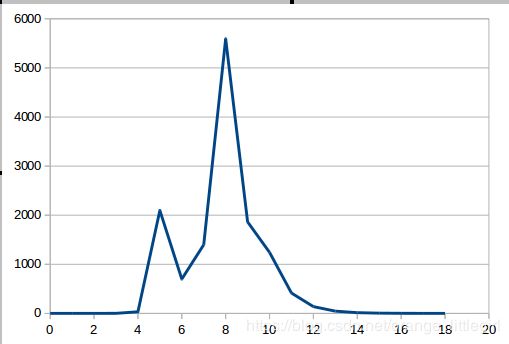
• （1）请绘制样例代码中LM 阻尼因子μ 随着迭代变化的曲线图。
  参考我以前的博文视觉slam14讲学习（四）之Ceres和G2O使用
  那篇博文是用高斯牛顿法求解的，具体原理：
  
• 我们现在要利用LM算法求解，具体原理：
  
• 阻尼因子作用：
  
• 阻尼因子迭代更新：
  
• 马夸尔特阻尼法

• ceres中LM求解器伪代码:
  
• 代码分析:

bool Problem::Solve(int iterations) {


    if (edges_.size() == 0 || verticies_.size() == 0) {
        std::cerr << "\nCannot solve problem without edges or verticies" << std::endl;
        return false;
    }

    TicToc t_solve;
    // 统计优化变量的维数，为构建 H 矩阵做准备
    SetOrdering();
    // 遍历edge, 构建 H = J^T * J 矩阵
    MakeHessian();
    // LM 初始化
    ComputeLambdaInitLM();
    // LM 算法迭代求解
    bool stop = false;
    int iter = 0;
    while (!stop && (iter < iterations)) {
        std::cout << "iter: " << iter << " , chi= " << currentChi_ << " , Lambda= " << currentLambda_
                  << std::endl;
        bool oneStepSuccess = false;
        int false_cnt = 0;
        while (!oneStepSuccess)  // 不断尝试 Lambda, 直到成功迭代一步
        {
            // setLambda
            AddLambdatoHessianLM();
            // 第四步，解线性方程 H X = B
            SolveLinearSystem();
            //
            RemoveLambdaHessianLM();

            // 优化退出条件1： delta_x_ 很小则退出
            if (delta_x_.squaredNorm() <= 1e-6 || false_cnt > 10) {
                stop = true;
                break;
            }

            // 更新状态量 X = X+ delta_x
            UpdateStates();
            // 判断当前步是否可行以及 LM 的 lambda 怎么更新
            oneStepSuccess = IsGoodStepInLM();
            // 后续处理，
            if (oneStepSuccess) {
                // 在新线性化点 构建 hessian
                MakeHessian();
                // TODO:: 这个判断条件可以丢掉，条件 b_max <= 1e-12 很难达到，这里的阈值条件不应该用绝对值，而是相对值
//                double b_max = 0.0;
//                for (int i = 0; i < b_.size(); ++i) {
//                    b_max = max(fabs(b_(i)), b_max);
//                }
//                // 优化退出条件2： 如果残差 b_max 已经很小了，那就退出
//                stop = (b_max <= 1e-12);
                false_cnt = 0;
            } else {
                false_cnt++;
                RollbackStates();   // 误差没下降，回滚
            }
        }
        iter++;

        // 优化退出条件3： currentChi_ 跟第一次的chi2相比，下降了 1e6 倍则退出
        if (sqrt(currentChi_) <= stopThresholdLM_)
            stop = true;
    }
    std::cout << "problem solve cost: " << t_solve.toc() << " ms" << std::endl;
    std::cout << "   makeHessian cost: " << t_hessian_cost_ << " ms" << std::endl;
    return true;
}

注意:
oneStepSuccess = IsGoodStepInLM();
//可能会出现rho无异常,跳出一次while,改变lambda
// 判断当前步是否可行以及 LM 的 lambda 怎么更新
//误差上升的时候,false,继续优化迭代;误差下降的时候,true,跳出循环记录下来

要记录完整的迭代lambda值必须把记录的方法写在第二个while()里面
record_lambdas.add(lambda_iter,currentLambda_);
lambda_iter++;

• 可视化结果(比写在外面多了7次迭代):
  

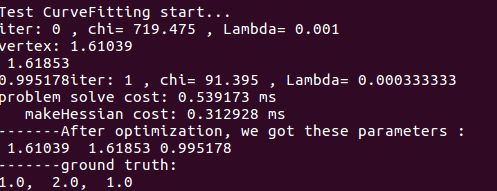
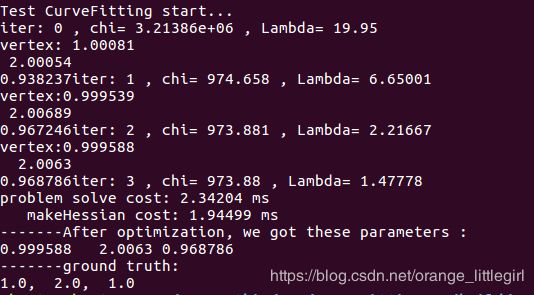
作业1.2

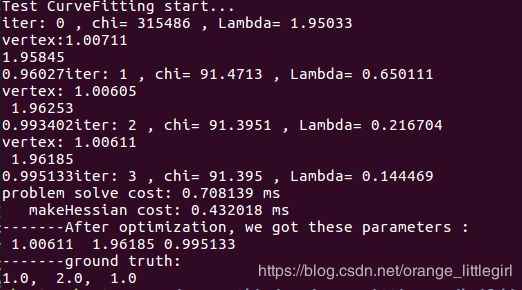
将曲线函数改成 y = ax 2 + bx + c,请修改样例代码中残差计算,雅克比计算等函数,完成曲线参数估计。

• 代码更改部分:

// 曲线模型的顶点，模板参数：优化变量维度和数据类型
class CurveFittingVertex: public Vertex
{
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW

    CurveFittingVertex(): Vertex(3) {}  // abc: 三个参数， Vertex 是 3 维的
    virtual std::string TypeInfo() const { return "abc"; }
};

// 误差模型 模板参数：观测值维度，类型，连接顶点类型
class CurveFittingEdge: public Edge
{
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW
    CurveFittingEdge( double x, double y ): Edge(1,1, std::vector{"abc"}) {
        x_ = x;
        y_ = y;
    }
    // 计算曲线模型误差
    virtual void ComputeResidual() override
    {
        Vec3 abc = verticies_[0]->Parameters();  // 估计的参数
        residual_(0) = ( abc(0)*x_*x_ + abc(1)*x_ + abc(2) ) - y_;  // 构建残差
    }

    // 计算残差对变量的雅克比
    virtual void ComputeJacobians() override
    {
        // Vec3 abc = verticies_[0]->Parameters();
        // double exp_y = std::exp( abc(0)*x_*x_ + abc(1)*x_ + abc(2) );

        Eigen::Matrix jaco_abc;  // 误差为1维，状态量 3 个(a,b,c)，所以是 1x3 的雅克比矩阵
        jaco_abc << x_ * x_ , x_  , 1 ;
        jacobians_[0] = jaco_abc;
    }
    /// 返回边的类型信息
    virtual std::string TypeInfo() const override { return "CurveFittingEdge"; }
public:
    double x_,y_;  // x 值， y 值为 _measurement
};

• 结果显示:
  
• 发现拟合效果较差
  初步分析是数据点太少,增加至1000之后,再次打印:
  
  还有一种方法,增加数据步子长度:double x = i/100.;改成double x=i/10.;
  

作业1.3

如果有实现其他阻尼因子更新策略可加分(选做)

• 代码迭代lambda策略分析及优化策略:
  
• 代码分析及优化:

bool Problem::IsGoodStepInLM() {
    double scale = 0;
    scale = delta_x_.transpose() * (currentLambda_ * delta_x_ + b_);
    scale += 1e-3;    // make sure it's non-zero :)

    // recompute residuals after update state
    // 统计所有的残差
    double tempChi = 0.0;
    for (auto edge: edges_) {
        edge.second->ComputeResidual();
        tempChi += edge.second->Chi2();//当前残差

    }

    double rho = (currentChi_ - tempChi) / scale;
    if (rho > 0 && isfinite(tempChi))   // last step was good, 误差在下降
    {
        double alpha = 1. - pow((2 * rho - 1), 3);
        alpha = std::min(alpha, 2. / 3.);
        double scaleFactor = (std::max)(1. / 3., alpha);
        currentLambda_ *= scaleFactor;
        ni_ = 2;// 控制 Lambda 缩放大小
        currentChi_ = tempChi;
        return true;
    } else {// 误差在上升
        currentLambda_ *= ni_;
        ni_ *= 2;
        return false;
    }

}

bool Problem::IsGoodStepInLM2() {


    // recompute residuals after update state
    // 统计所有的残差
    double tempChi = 0.0;
    for (auto edge: edges_) {
        edge.second->ComputeResidual();
        tempChi += edge.second->Chi2();//当前残差

    }

    double frac1 = delta_x_.transpose()* b_;
    double alpha = frac1 / (((tempChi - currentLambda_)/2) + 2*frac1);

    RollbackStates();
    delta_x_ *= alpha;
    UpdateStates();

    double scale = 0;
    scale = delta_x_.transpose() * (currentLambda_ * delta_x_ + b_);
    scale += 1e-3;

    double rho = (currentChi_ - tempChi) / scale;

    //迭代策略2
    if (rho > 0 && isfinite(tempChi))   // last step was good, 误差在下降
    {
        currentLambda_ = std::max(currentLambda_/(1. + alpha), 1e-7);
        currentChi_ = tempChi;
        return true;
    } else {// 误差在上升
        currentLambda_ += abs(tempChi - currentChi_)/(2.*alpha);
        return false;
    }

}

2.作业2

公式推导,根据课程知识,完成 F, G 中如下两项的推导过程:

3.作业3

证明公式9:

作业2&3的解答: