数值计算 复合梯形公式、复合辛普森公式、龙贝格序列、自适应辛普森Python实现(不调用函数库)

概念介绍

复合梯形公式

将区间$[a,b]$ 划分 $n$ 等分，分点 $x_k=a+kh$ ，$h=\frac{b-a}{n}$ ，$k=0,1,...,n$，在每个子区间$[x_k,x_k+1]]$上采用梯形公式，则得
$$T_n=\frac{h}{2}\sum _{k=0}^{n-1}[f(x_k)+f(x_{k+1})]$$

复合辛普森公式

将区间$[a,b]$ 划分 $n$ 等分，分点 $x_k=a+kh$ ，$h=\frac{b-a}{n}$ ，$k=0,1,...,n$，在每个子区间$[x_k,x_k+1]]$上采用辛普森公式，并记$x_{k+1/2}=x_k+\frac{1}{2}h$，则得
$$S_n=\frac{h}{6}\sum _{k=0}^{n-1}[f(x_k)+4f(x_{k+1/2}+f(x_{k+1}))]$$

龙贝格序列

设以$T_0^{(k)}$表示二分$k$次后求得的梯形值，且以$T_m^{(k)}$表示序列的第$m$次加速值，则依递推公式可得
$$T_m^{(k)}=\frac{4^m}{4^m-1}{T}_{m-1}^{(k+1)}-\frac{1}{4^m-1}{T}_{m-1}^{(k)}$$

自适应辛普森公式

就是先对被积函数计算辛普森公式值，然后计算二分后两个区间的辛普森公式值的和，如果小于期望误差值则继续二分，对满足要求的区间不再二分，直到误差小于期望值。
这里重点提一下，大家可能在某些地方会看到在计算精度和积分值的时候会有15之类的字样，有人说是误差修正，个人理解是做了一次外推加速。

代码实现

目的是计算${\int }_0^1\sqrt{x}ln(x)dx$

import numpy as np
import matplotlib.pyplot as plt
import pylab as mpl

def func(x_: float):
    if x_ == 0:
        return 0
    else:
        return np.sqrt(x_) * np.log(x_)
        # return 1/x_


def CTR(start: float, end: float, n: int):
    h = (end - start) / n
    x = [start + k * h for k in range(0, n + 1)]
    return h / 2 * sum(func(x[k]) + func(x[k + 1]) for k in range(0, n))


def CSR(start: float, end: float, n: int):
    h = (end - start) / n
    x = [start + k * h for k in range(0, n + 1)]
    return h / 6 * sum(func(x[k]) + 4 * func(x[k] + 1 / 2 * h) + func(x[k + 1]) for k in range(0, n))


def RA(start: float, end: float, k: int):
    I_table = [CTR(start, end, 2 ** _) for _ in range(k + 1)]
    # print(I_table)
    for i in range(k):
        m = i + 1
        for j in range(len(I_table) - 1, m-1, -1):
            I_table[j] = (4 ** m / (4 ** m - 1)) * I_table[j] - 1 / (4 ** m - 1) * I_table[j-1]
        # print(I_table)
    return I_table[len(I_table)-1]


def CSR_AQ(start: float, end:float, eps:float): #递归计算
    # print(1)
    mid = (start + end) / 2
    S = CSR(start, end, 1)
    # print(S)
    Sleft = CSR(start, mid, 1)
    Sright = CSR(mid, end, 1)
    # print(Sleft+Sright-S)
    if abs(Sleft+Sright-S) <= eps:
        return Sleft + Sright
    else:
        return CSR_AQ(start, mid, eps/2) + CSR_AQ(mid, end, eps/2)





def draw(start: float, end: float):
    ans_ctr = []
    ans_csr = []
    ans_r = []
    h_r = []
    h = []
    for i in range(1, 129):
        h.append(1 / i)
        if i==1:
            h_r.append(1)
        else:
            h_r.append(1 / 2**int(np.log2(i)))
            # print(int(np.log2(i)))
        ans_r.append(RA(start, end, int(np.log2(i))))
        ans_ctr.append(CTR(start, end, i))
        ans_csr.append(CSR(start, end, i))
    plt.plot(h, ans_ctr, label="复合梯形", color='red')
    plt.plot(h, ans_csr, label="复合辛普森", color='blue')
    plt.plot(h_r, ans_r, label="龙贝格序列", color='green')
    plt.axhline(-4 / 9, label="精确值", color='black')
    plt.xticks(np.arange(0, 1, 0.1))
    plt.yticks(np.arange(0, -0.5, -0.05))
    plt.legend(loc="upper left")
    plt.title("积分逼近")
    mpl.rcParams['font.sans-serif'] = ['SimHei']
    mpl.rcParams['axes.unicode_minus'] = False
    plt.show()


if __name__ == "__main__":
    rv = -4 / 9
    print("精确值:", -4 / 9)

    for i in range(1, 5):
        ans_ctr = CTR(0, 1, i)
        ans_csr = CSR(0, 1, i)
        print("T_%d:" % i, ans_ctr, "步长:", 1 / i, "绝对误差:", abs(rv - ans_ctr))
        print("S_%d:" % i, ans_csr, "步长:", 1 / i, "绝对误差:", abs(rv - ans_csr))
        print("\n")

    for i in range(1, 15):
        ans_ra = RA(0, 1, i)
        print("T^%d:" % i, ans_ra, "步长:", 1 / 2 ** i, "绝对误差:", abs(rv - ans_ra))

    print("\n")
    ans_csr_aq = CSR_AQ(0, 1, 1e-4)
    print("S_A:", ans_csr_aq, "绝对误差:", abs(rv - ans_csr_aq))

    draw(0, 1)

结果展示

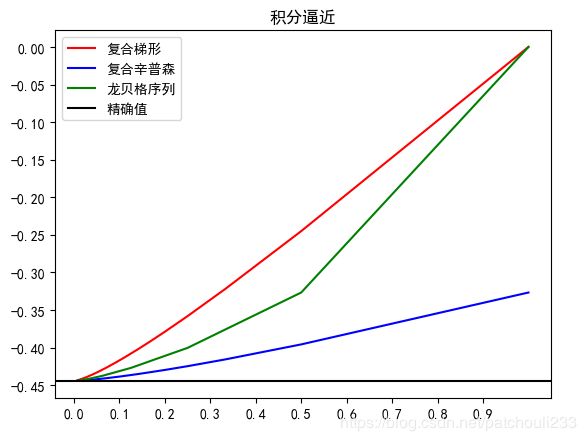
这个自己跑一下就行，参数都是作业需要。
这里就解释一下上图是各公式所得积分值随步长变化的曲线图，由于龙贝格序列要求区间数为$2^n$，所以取的点会少一点。