随机森林基本原理与算法描述
一. 前言
在前几篇博文中我们介绍了boosting系列的几个主要算法GBDT、AdaBoost和XGboost的基本原理与算法描述。本篇博文将介绍集成学习的另一大分支bagging方法的代表算法随机森林（Random Forest）算法。
bagging系列的算法原理相较于boosting系列的算法要简单不少。bagging方法各个子树并行的生成，而不像boosting系列算法，下一棵子树的形成是建立在上一棵的基础之上的。bagging方法使用强学习器作为基学习器的时候效果会更好，这也是防止过拟合的一种方式，而boosting方法使用弱学习器作为基学习器的时候效果会更好。
本文的主要内容：首先介绍随机森林的基本原理，然后再介绍随机森林家族中的其他一些方法，接着会讨论关于方差与偏差的问题以及方差和偏差是如何影响着我们的机器学习模型，最后总结随机森林的优缺点。
下面我们就开始介绍随机森林吧！
二. 随机森林算法基本原理介绍
2.1 随机森林简单介绍
随机森林是在bagging算法的基础之上加了一点小小的改动演化过来的。我们知道bagging算法是在原始的数据集上采用有放回的随机取样的方式来抽取m个子样本，从而利用这m个子样本训练m个基学习器，从而降低了模型的方差。而我们的随机森林的改动有两处，第一：不仅随机的从原始数据集中随机的抽取m个子样本，而且在训练每个基学习器的时候，不是从所有特征中选择最优特征来进行节点的切分，而是随机的选取k个特征，从这k个特征中选择最优特征来切分节点，从而更进一步的降低了模型的方差；第二：随机森林使用的基学习器是CART决策树。
随机森林随机选择的样本子集大小m越小模型的方差就会越小，但是偏差会越大，所以在实际应用中，我们一般会通过交叉验证的方式来调参，从而获取一个合适的样本子集的大小。所以随机森林除了基学习器使用CART决策树和特征的随机选择以外，其他方面与bagging方法没有什么不同。
2.2 随机森林的算法描述
输入：训练数据集
，样本子集的个数T
输出：最终的强分类器
（1）对
:
（a）从原始样本集中随机的抽取m个样本点，得到一个训练集
;
（b）用训练集，训练一个CART决策树，这里在训练的过程中，对每个节点的切分规则是先从所有特征中随机的选择k个特征，然后在从这k个特征中选择最优的切分点在做左右子树的划分。
（2）如果是分类算法，则预测的最终类别为该样本点所到叶节点中投票数最多的类别；如果是回归算法，则最终的类别为该样本点所到叶节点的均值。
注意：我们随机森林的基学习器并不是弱学习器而是强学习器，是有很高深度的强决策树组成的，为什么基学习器是强学习器，我们会在下面从另一个角度来说明。
随机森林的基本原理与算法描述介绍完毕，接下来我们就介绍一下，随机森林的推广Extremely Randomized Trees和Isolation Forest。
三. 随机森林家族的其它成员
3.1 Extremely Randomized Trees介绍
Extremely Randomized Trees（以下简称extra trees）是RF的一个变种, 原理几乎和RF一模一样，仅有区别有：
（1）对于每个决策树的训练集，RF采用的是随机采样bootstrap来选择子集作为每个决策树的训练集，而extra trees一般不采用随机采样，即每个决策树采用原始训练集。
（2）在选定了划分特征后，RF的决策树会基于信息增益，基尼系数，均方差之类的原则，选择一个最优的特征值划分点，这和传统的决策树相同。但是extra trees比较的激进，他会随机的选择一个特征值来划分决策树。
从第二点可以看出，由于随机选择了特征值的划分点位，而不是最优点位，这样会导致生成的决策树的规模一般会大于RF所生成的决策树。也就是说，模型的方差相对于RF进一步减少，但是偏差相对于RF进一步增大。在某些时候，extra trees的泛化能力比RF更好。
3.2 Isolation Forest介绍
Isolation Forest（以下简称iForest）是南大周志华老师的团队在2008年提出的，它是一个在高维数据集中使用随机的森林有效的进行异常值检测的方法。iForest有如下的特点：
（1）iForest用部分模型不隔离所有正常点的情况下效果很好，并且模型的建立仅使用很小的样本数量（子采样数量远远小于原始训练集的数量），因为iForest目标是异常点检测，只需要部分样本就可以将异常点区分出来；
（2）iForest中的树的建立是任意选择一个特征，然后在该特征中任意选择一个值作为划分左右子树的标准；
（3）iForest使用不放回的随机子采样策略；
对于异常点的判断，用训练好的iForest预测样本点
。计算该样本点落在每棵树上的叶子节点的深度。从而可以计算出iForest中该样本点所在的所有叶子节点的平均高度
。此时我们用下面的公式计算样本点的异常概率：
其中，n为样本个数，
的表达式为：
， 
（a）当接近于时，
接近于0.5；
（b）当接近于0时，接近于1；
（c）当接近于n-1时，接近于0；
所以根据上面可以得到如下的结论：
（a）如果样本点的预测越接近于1，则该样本点就越有可能为异常点；
（b）如果样本点的预测小于0.5，则它被视为正常点是比较安全的；
（c）如果样本点的预测接近0.5，则该点不能被判断是否为异常点。
到这里，关于随机森林及其家族其他成员已经简单介绍完毕。下面我们将探讨一个有趣的问题。
四. 为什么用xgboost/gbdt/Adaboost在调参的时候把树的最大深度调成6就有很高的精度了，但是用RandomForest的时候需要把树的深度调到15或更高。
在回答这个问题之前我们先介绍一下在机器学习中方差与偏差的概念。了解不同的误差来源是如何导致偏差和方差的，有助于我们改进数据拟合过程，从而获得更精确的模型。下面我们将从是三个方面介绍偏差和方差。
（1）从概念上：
（a）误差来源于偏差。误差来源于偏差是我们的模型的预测值与真实值之间的差异。意思就是我们的数据集在拟合的好不好。所以想要拟合的好必须要有第偏差，而偏差越低，我们的模型就越复杂，就会更容易的过拟合。
（b）误差来源于方差。误差来源于方差是给定数据点模型预测的变化性。意思就是模型在测试集上的表现如何，想要模型的泛化能力好那么就必须要低方差，而方差越低模型越简单，就会容易造成欠拟合。
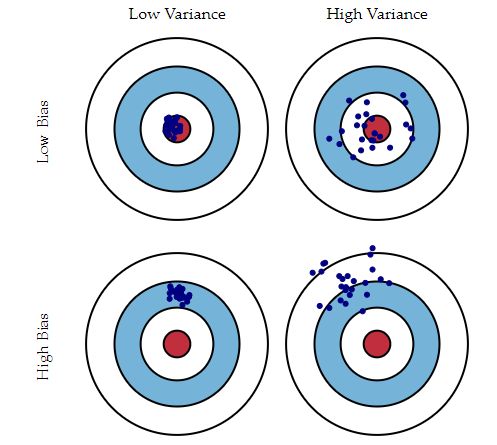
（2）从图形上：
从上图可以看出，数据里靶心越近说明数据的拟合的越好偏差越低；数据越分散说明方差越大。而我们在机器学习中的目标就是尽量的做到低偏差的同时也要低方差。这样我们模型在训练集上拟合的很好，在测试集上的泛化能力也好。
（3）从数学公式上：
![Err(x)=E[(Y-\hat{f}(x))^2]=(E[\hat{f}(x)]-f(x))^2+E[(\hat{f}(x)-E[\hat{f}(x)])^2]+\sigma {_{e}}^2](http://img.e-com-net.com/image/info8/d913ea3a060a4ea580a1d32aac123ad8.gif){kind=small}
上式中，
表示我们模型的总误差，右边第一项表示模型偏差的平方，第二项表示模型的方差，第三项表示模型本身就具有的误差，是一个常数。所以我们的目标就是最小化上式，最好的办法就是同时使
和V
。而要使它们为0，则需要一个正确的模型和无限的数据集去调整它们，这在现实中是不可能的，所以我们的只能尽量的最小化它们。
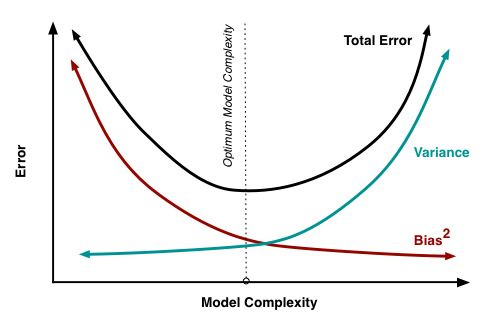
在上图中我们可以看到模型越复杂的模型的偏差越小而方差越大，模型越简单模型的偏差越大而方差越小，所以对于模型的偏差与方差我们需要对它们进行一个权衡。
接下来回到我们的问题中，对于boosting系列的算法我们说过，boosting的基本思想是在每次迭代中生成的一个弱学习器是基于前一个弱学习器的表现来的，即在boosting算法中我们弱学习器的构造都是一步步的减小样本的偏差，使我们的最终强学习器的偏差很小，而导致更高的方差，所我们需要更简单的基学习器来使我们的模型更加的简单，从而降低模型的方差。而在随机森林算法中，我们随机的抽取子样本和随机的选择特征来构建决策树，使我们的生成的模型的方差会很小，但是由于每个基学习器使用的数据不全，这造成了相对较大的偏差，所以我们的随机森林的基学习器一般使用的是强学习器，即决策树的深度很高，目的就是为了增加模型的复杂度，降低模型的偏差。所以我们在boosting系列算法中我们把树的深度设置的很小，而在随机森林算啊中我们把树的深度设置的很大。
五. 随机森林优缺点
优点：
（1）训练可以高度并行化，对于大数据时代的大样本训练速度有优势；
（2） 由于可以随机选择决策树节点划分特征，这样在样本特征维度很高的时候，仍然能高效的训练模型；
（3）在训练后，可以给出各个特征对于输出的重要性（在sklearn中有方法feature_importances_可以输出特征的重要性）；
（4）由于采用了随机采样，训练出的模型的方差小，泛化能力强；
（5）相对于Boosting系列的Adaboost和GBDT等， RF实现比较简单；
（6）对部分特征缺失不敏感。
缺点：
（1）在某些噪音比较大的样本集上，RF模型容易陷入过拟合；
（2）取值划分比较多的特征容易对RF的决策产生更大的影响，从而影响拟合的模型的效果。
六. 参考文献/博文
（1）L. Breiman, “Random Forests”, Machine Learning, 45(1), 5-32, 2001.
（2）IsoLation Forest原论文
（3）了解模型的偏差与方差
（4）比较好的博客
（5）sklearn官方网站