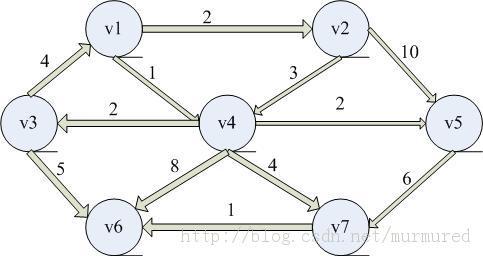
最短路径
最短路算法详解(dijkstra/SPFA/floyd)
一、Dijkstra
Dijkstra单源最短路算法,即计算从起点出发到每个点的最短路。所以Dijkstra常常作为其他算法的预处理。
使用邻接矩阵的时间复杂度为O(n^2),用优先队列的复杂度为O(mlogn)
(一) 过程
每次选择一个未访问过的到已经访问过(标记为Known)的所有点的集合的最短边,并用这个点进行更新,过程如下:
Dv为最短路,而Pv为前面的顶点。
1. 初始
| V |
Known |
Dv |
Pv |
| V1 |
F |
0 |
0 |
| V2 |
F |
∞ |
0 |
| V3 |
F |
∞ |
0 |
| V4 |
F |
∞ |
0 |
| V5 |
F |
∞ |
0 |
| V6 |
F |
∞ |
0 |
| V7 |
F |
∞ |
0 |
2. 在v1被标记为已知后的表
| V |
Known |
Dv |
Pv |
| V1 |
T |
0 |
0 |
| V2 |
F |
2 |
V1 |
| V3 |
F |
∞ |
0 |
| V4 |
F |
1 |
V1 |
| V5 |
F |
∞ |
0 |
| V6 |
F |
∞ |
0 |
| V7 |
F |
∞ |
0 |
3. 下一步选取v4并且标记为known,顶点v3,v5,v6,v7是邻接的顶点,而他们实际上都需要调整。如表所示:
| V |
Known |
Dv |
Pv |
| V1 |
T |
0 |
0 |
| V2 |
F |
2 |
V1 |
| V3 |
F |
3 |
V4 |
| V4 |
T |
1 |
V1 |
| V5 |
F |
3 |
V4 |
| V6 |
F |
9 |
V4 |
| V7 |
F |
5 |
V4 |
4. 接下来选取v2,v4是邻接点,但已经是known的,不需要调整,v5是邻接的点但不做调整,因为经过v2的值为2+10=12而长为3的路径已经是已知的。
| V |
Known |
Dv |
Pv |
| V1 |
T |
0 |
0 |
| V2 |
T |
2 |
V1 |
| V3 |
F |
3 |
V4 |
| V4 |
T |
1 |
V1 |
| V5 |
F |
3 |
V4 |
| V6 |
F |
9 |
V4 |
| V7 |
F |
5 |
V4 |
5. 接下来选取v5,值为3,v7 3+6>5不需调整,然后选取v3,对v6的距离下调到3+5=8
| V |
Known |
Dv |
Pv |
| V1 |
T |
0 |
0 |
| V2 |
T |
2 |
V1 |
| V3 |
T |
3 |
V4 |
| V4 |
T |
1 |
V1 |
| V5 |
T |
3 |
V4 |
| V6 |
F |
8 |
V3 |
| V7 |
F |
5 |
V4 |
6. 再选下一个顶点是v7,v6变为5+1=6
| V |
Known |
Dv |
Pv |
| V1 |
T |
0 |
0 |
| V2 |
T |
2 |
V1 |
| V3 |
T |
3 |
V4 |
| V4 |
T |
1 |
V1 |
| V5 |
T |
3 |
V4 |
| V6 |
F |
6 |
V7 |
| V7 |
T |
5 |
V4 |
7. 最后选取v6
| V |
Known |
Dv |
Pv |
| V1 |
T |
0 |
0 |
| V2 |
T |
2 |
V1 |
| V3 |
T |
3 |
V4 |
| V4 |
T |
1 |
V1 |
| V5 |
T |
3 |
V4 |
| V6 |
T |
6 |
V7 |
| V7 |
T |
5 |
V4 |
(二) 局限性
Dijkstra没办法解决负边权的最短路径,如图
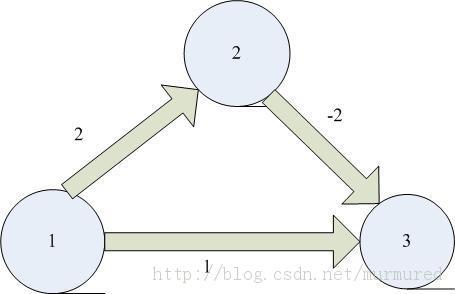
运行完该算法后,从顶点 1 到顶点 3 的最短路径为 1,3 ,其长度为 1 ,而实际上最短路径为 1,2,3 ,其长度为 0. (因为过程中先选择 v3 , v3 被标记为已知,今后不再更新)
(三) 算法实现。
1 .普通的邻接表 以(HDU 1874 畅通工程续 SPFA || dijkstra)为例
用vis作为上面标记的known,dis记录最短距离(记得初始化为一个很大的数)。
void dijkstra(int s)
{
memset(vis,0,sizeof(vis));
int cur=s;
dis[cur]=0;
vis[cur]=1;
for(int i=0;ifor(int j=0;jif(!vis[j] && dis[cur] + map[cur][j] < dis[j]) //未被标记且比已知的短,可更新
dis[j]=dis[cur] + map[cur][j] ;
int mini=INF;
for(int j=0;jif(!vis[j] && dis[j] < mini) //选择下一次到已知顶点最短的点。
mini=dis[cur=j];
vis[cur]=true;
}
} 要重载个比较函数。
struct point
{
int val,id;
point(int id,int val):id(id),val(val){}
bool operator <(const point &x)const{
return val>x.val;
}
};
void dijkstra(int s)
{
memset(vis,0,sizeof(vis));
for(int i=0;i q;
q.push(point(s,0));
vis[s]=true;
dis[s]=0;
while(!q.empty())
{
int cur=q.top().id;
q.pop();
vis[cur]=true;
for(int i=head[cur];i!=-1;i=e[i].next)
{
int id=e[i].to;
if(!vis[id] && dis[cur]+e[i].val < dis[id])
{
dis[id]=dis[cur]+e[i].val;
q.push(point(id,dis[id]));
}
}
}
}
二、SPFA(bellman-ford)
SPFA是bellman-ford的改进算法(队列实现),效率也更高,故直接介绍SPFA。
相比于Dijkstra,SPFA可以计算带负环的回路。
邻接表的复杂度为:O(kE)E为边数,k一般为2或3
(一)原理过程:
bellman-ford算法的基本思想是,对图中除了源顶点s外的任意顶点u,依次构造从s到u的最短路径长度序列dist[u],dis2[u]……dis(n-1)[u],其中n是图G的顶点数,dis1[u]是从s到u的只经过1条边的最短路径长度,dis2[u]是从s到u的最多经过G中2条边的最短路径长度……当图G中没有从源可达的负权图时,从s到u的最短路径上最多有n-1条边。因此,
dist(n-1)[u]就是从s到u的最短路径长度,显然,若从源s到u的边长为e(s,u),则dis1[u]=e(s,u).对于k>1,dis(k)[u]满足如下递归式,dis(k)[u]=min{dis(k-1)[v]+e(v,u)}.bellman-ford最短路径就是按照这个递归式计算最短路的。
SPFA的实现如下:用数组dis记录更新后的状态,cnt记录更新的次数,队列q记录更新过的顶点,算法依次从q中取出待更新的顶点U,按照dis(k)[u]的递归式计算。在计算过程中,一旦发现顶点K有cnt[k]>n,说明有一个从顶点K出发的负权圈,此时没有最短路,应终止算法。否则,队列为空的时候,算法得到G的各顶点的最短路径长度。
1.邻接矩阵的SPFA 以(HDU 1874 畅通工程续 SPFA || dijkstra)为例
void SPFA(int s)
{
for(int i=0;ibool vis[MAXN]={0};
vis[s]=true;
dis[s]=0;
queue<int> q;
q.push(s);
while(!q.empty())
{
int cur=q.front();
q.pop();
vis[cur]=false;
for(int i=0;iif(dis[cur] + map[cur][i] < dis[i])
{
dis[i]=dis[cur] + map[cur][i];
if(!vis[i])
{
q.push(i);
vis[i]=true;
}
}
}
}
} 2.邻接表的SPFA(推荐) 以(HDU 1874 畅通工程续 SPFA || dijkstra)为例
void spfa(int s)
{
memset(vis,0,sizeof(vis));
for(int i=0;iint> q;
q.push(s);
vis[s]=true;
dis[s]=0;
while(!q.empty())
{
int cur=q.front();
q.pop();
vis[cur]=false;
for(int i=head[cur];i!=-1;i=e[i].next)
{
int id=e[i].to;
if(dis[id] > dis[cur]+e[i].val)
{
dis[id] = dis[cur] + e[i].val;
if(!vis[id])
{
vis[id]=true;
q.push(id);
}
}
}
}
}
bool spfa()
{
for(int i=0;i<=n;i++)
dis[i]=INF;
bool vis[MAXN]={0};
int cnt[MAXN]={0};
queue<int> q;
dis[0]=0;
vis[0]=true;
cnt[0]=1;
q.push(0);
while(!q.empty())
{
int cur=q.front();
q.pop();
vis[cur]=false;
for(int i=head[cur];i!=-1;i=e[i].next)
{
int id=e[i].to;
if(dis[cur] + e[i].val > dis[id])
{
dis[id]=dis[cur]+e[i].val;
if(!vis[id])
{
cnt[id]++;
if(cnt[cur] > n)
return false;
vis[id]=true;
q.push(id);
}
}
}
}
return true;
} (三):优化
SLF(Small Label First)是指在入队时如果当前点的dist值小于队首, 则插入到队首, 否则插入到队尾。
LLL不太常用,我也没研究。
眼见的同学应该发现了,上面的差分约束四个字,是的SPFA可以很好的实现差分约束系统。
近几天会把差分约束也整理出来~
三、floyd
全称Floyd-Warshall。记得离散数学里面有Warshall算法,用来计算传递闭包。而数据结构每次都简称floyd,当时就觉得两个都差不多,有神马关系,后来google一下发现是同一个算法。。。。改个名字出来走江湖啊!!!!!
这个算法用于求所有点对的最短距离。比调用n次dijkstra的优点在于代码简单。
时间复杂度为O(n^3)
(一)原理过程:这是一个dp(动态规划的过程)
dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
即从顶点i到j且经过顶点k的最短路径长度。
(二)实现: 以(HDU 1874 畅通工程续 SPFA || dijkstra)为例
void floyd()
{
for(int k=0;kfor(int i=0;ifor(int j=0;j 四、其他
如走迷宫经常用的BFS,以一个点出发,向外扩散。
如:
UVA 10047 - TheMonocycle BFS
HDU 1728 逃离迷宫 BFS
POJ3984 迷宫问题 BFS
UVA 11624 - Fire! 图BFS
除了上面的
HDU 1874 畅通工程续 SPFA || dijkstra||floyd
还有:
UVA11280 - Flying to Fredericton SPFA 变形
UVA11090 - Going in Cycle!! SPFA
UVA10917 Walk Through the Forest SPFA
POJ 3259Wormholes 邻接表的SPFA 判断负权回路
POJ 1932XYZZY (ZOJ 1935)SPFA+floyd
UVA11374 Airport Express SPFA||dijkstra
UVA11367 - Full Tank? dijkstra+DP
POJ 1511Invitation Cards (ZOJ 2008) 使用优先队列的dijkstra
POJ 3268Silver Cow Party (Dijkstra~)
POJ 2387Til the Cows Come Home (Dijkstra)
UVA10603 - Fill BFS~