《统计学习方法》第7章 课后习题

这一章尤为复杂，我看了好多资料还有博客，数学功底差总是吃亏的

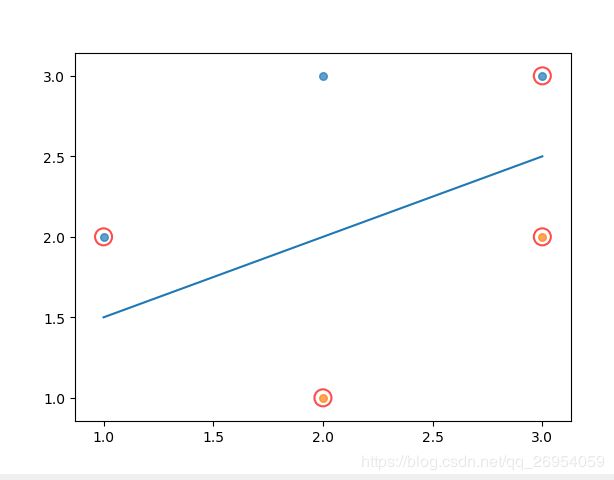
1.1 比较感知机的对偶形式与线性可分支持向量机的对偶形式。

可以根据线性向量机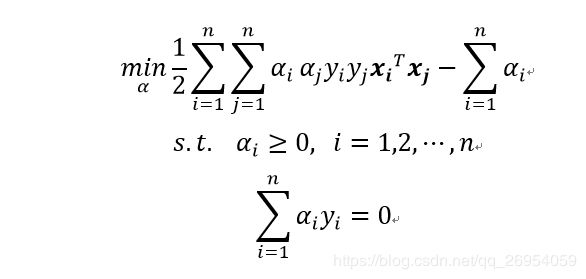：求解，这边我直接只用自己写的程序求解。w,b为

https://cuijiahua.com/blog/2017/11/ml_8_svm_1.html 这网站很不错，讲解的很清楚

转载注明：机器学习实战教程（八）：支持向量机原理篇之手撕线性SVM | Jack Cui

自己写的程序很有问题，只是能来对算法流程加深印象，程序性能并不好

#-*- coding:UTF-8 -*-
import matplotlib.pyplot as plt
import numpy as np

class SVM:
    def __init__(self,datamat,labelmat,model='RBF'):
        self.X = datamat
        self.Y = labelmat
        #实验时得出
        #在非线性时30-33会有最好效果，我参考的代码能达到0.04的错误率，我只能0.06的，应该是选择alpha1，2时有些问题
        #但在线性时将会因松弛因子大将所有xi都考虑，过拟合
        self.C = 33.0 if model == 'RBF' else 0.02
        self.N,self.M = np.array(self.X).shape
        self.alpha = np.array([0.0]*self.N)
        self.b = 0.0
        self.model = model
        self.updateTrainParam()  
    
    #推导L(w,b,a)时xi的转置是由w的转置带过来的，书中默认有
    #注意所有xi输入时已经是xi的转置了
    def K(self,xi,xj,e=0.1):
        #np中矩阵转置，[1,2,3]没有转置 一维[[1,2,3]]^T = 三维[[1],[2],[3]]
        #由于[]取值方便，在这里进行转换
        xi_arr = np.array([xi])
        xj_arr = np.array([xj])        
        if self.model == 'liner':
            #这时点乘为一个数，但依旧是矩阵表示 [[]]
            return (xi_arr.dot(xj_arr.T))[0][0]
        #高斯核函数
        elif self.model == 'RBF':
            x = xi_arr-xj_arr
            return np.exp(x.dot(x.T)/(-1*e**2))[0][0]
    #计算g(xi)          
    def computGx(self,i):
        gxi = 0.0
        for j in range(self.N):
            gxi += self.alpha[j]*self.Y[j]*self.K(self.X[j], self.X[i])    
        return gxi+self.b
    #计算yi*g(xi)
    def computyMg(self,i):
        return self.Y[i]*self.Gx[i]
    #是否满足kkt条件
    def KKT(self,i):
        if self.alpha[i] == 0:
            return self.computyMg(i) >= 1
        elif 0 < self.alpha[i] < self.C:
            return self.computyMg(i) == 0
        else:
            return self.computyMg(i) <= 1
    #计算误差Ei
    def computEi(self,i):
        return self.Gx[i] - self.Y[i]
    #名字取错，由于不用全部重新更新，只调用一次初始化
    def updateTrainParam(self):
        self.Gx = [self.computGx(i) for i in range(self.N)]
        self.Ei = [self.computEi(i) for i in range(self.N)]    
       
    
    #不使用精度，限制迭代次数
    def train(self,max_itar,rate):  
        #计算上下限L,H
        def computLH(i,j):
            L = 0.0
            H = 0.0
            s = self.alpha[j]-self.alpha[i]
            a = self.alpha[j]+self.alpha[i]
            if self.Y[i] == self.Y[j]:
                L = max([0,a-self.C])
                H = min([self.C,a])
            else:
                L = max([0,s])
                H = min([self.C,self.C+s]) 
            return L,H
        #计算a2new,unc
        def computAlp2newunc(i,j):
            n = self.K(self.X[i], self.X[i])+self.K(self.X[j], self.X[j])-2*self.K(self.X[i], self.X[j])
            return self.alpha[j] + self.Y[j]*(self.Ei[i] - self.Ei[j])/n
        #计算a2new
        def computAlp2new(i,j):
            a2newunc = computAlp2newunc(i, j)
            L,H = computLH(i, j)
            if a2newunc > H:
                return H
            elif a2newunc < L:
                return L
            else:
                return a2newunc
        #计算a1new,a2new
        def computA1A2new(i,j):
            a2new = computAlp2new(i, j)
            a1new = self.alpha[i] + self.Y[i]*self.Y[j]*(self.alpha[j]-a2new)
            return a1new,a2new
        #计算a1new,a2new,bnew
        def computAllnew(i,j):
            bnew = 0.0
            a1new,a2new = computA1A2new(i,j)
            b1new = -self.Ei[i]-self.Y[i]*self.K(self.X[i], self.X[i])*(a1new - self.alpha[i])\
                -self.Y[j]*self.K(self.X[i], self.X[j])*(a2new - self.alpha[j])+self.b 
            b2new = -self.Ei[j]-self.Y[i]*self.K(self.X[i], self.X[j])*(a1new - self.alpha[i])\
                -self.Y[j]*self.K(self.X[j], self.X[j])*(a2new - self.alpha[j])+self.b            
            if 0< a1new < self.C:
                bnew = b1new
            elif 0< a2new < self.C:   
                bnew = b2new 
            else:
                bnew = (b1new+b2new)/2  
            return a1new,a2new,bnew
        
        #训练开始处     
        for k in range(max_itar):
            #外循环列表
            supvet_indx = [i for i in range(self.N) if 0< self.alpha[i] 0:
                    j = self.Ei.index(min(self.Ei))
                else:
                    j = self.Ei.index(max(self.Ei))
                #4.a1!=a2 
                if i == j:
                    continue
                a2old = self.alpha[j]
                #计算a1new,a2new,bnew
                a1new,a2new,bnew = computAllnew(i, j)
                #a2的变化率足够小
                if(abs(a2old - a2new) < rate):
                    break  
                #更新a1,a2,b
                self.alpha[i] = a1new
                self.alpha[j] = a2new
                self.b = bnew

                #更新G(x)和Ei,减少计算
                self.Gx[i] = self.computGx(i)
                self.Gx[j] = self.computGx(j)                
                self.Ei[i] = self.computEi(i)
                self.Ei[j] = self.computEi(j)
            print(k)
    #计算w        
    def computW(self):
        w =  np.array([[0.0]*self.M])
        X = np.array(self.X)
        for i in range(self.N):
            w += self.alpha[i]*self.Y[i]*X[i]
        return w[0]
    #预测分数
    def predict(self,X_test,Y_test):
        def K_arr(xi):
            return np.array([[self.K(xi, xj) for xj in self.X]])
        
        err_count = 0
        for i,xi in enumerate(X_test):
            
            Karr = K_arr(xi)
            fsign = np.sign(Karr.dot(np.array([self.Y*self.alpha]).T)[0][0]+self.b)
            if fsign != Y_test[i]:
                err_count += 1
                
        return err_count/self.N
    

def loadDataSet(filename):
    datamat = []
    labelmat = []
    with open(filename) as fr:
        for line in fr.readlines():
            lineArr = line.strip().split('\t')
            datamat.append([float(lineArr[0]),float(lineArr[1])])
            labelmat.append(float(lineArr[2]))
            
    return datamat,labelmat

def showDataSet(dataMat,labelMat):
    data_plus = []
    data_minus = []
    for i in range(len(dataMat)):
        if labelMat[i] > 0:
            data_plus.append(dataMat[i])
        else:
            data_minus.append(dataMat[i])
            
    data_plus_np = np.array(data_plus)
    data_minus_np = np.array(data_minus)
    plt.scatter(np.transpose(data_plus_np)[0],np.transpose(data_plus_np)[1])
    plt.scatter(np.transpose(data_minus_np)[0],np.transpose(data_minus_np)[1])
    plt.show()
    
def showClassifer(dataMat, labelMat,w, b,alphas):
    #绘制样本点
    data_plus = []                                  #正样本
    data_minus = []                                 #负样本
    for i in range(len(dataMat)):
        if labelMat[i] > 0:
            data_plus.append(dataMat[i])
        else:
            data_minus.append(dataMat[i])
    data_plus_np = np.array(data_plus)              #转换为numpy矩阵
    data_minus_np = np.array(data_minus)            #转换为numpy矩阵
    plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1], s=30, alpha=0.7)   #正样本散点图
    plt.scatter(np.transpose(data_minus_np)[0], np.transpose(data_minus_np)[1], s=30, alpha=0.7) #负样本散点图
    #绘制直线
    x1 = max(dataMat)[0]
    x2 = min(dataMat)[0]
    a1, a2 = w
    b = float(b)
    a1 = float(a1)
    a2 = float(a2)
    y1, y2 = (-b- a1*x1)/a2, (-b - a1*x2)/a2
    plt.plot([x1, x2], [y1, y2])
    #找出支持向量
    for i, alpha in enumerate(alphas):
        if alpha > 0:
            x, y = dataMat[i]
            plt.scatter([x], [y], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolor='red')
    plt.show()
    
def main():
    #习题2    
    x=[[1, 2], [2, 3], [3, 3], [2, 1], [3, 2]]
    y=[1, 1, 1, -1, -1]
    svm_lin = SVM(x, y,'liner')
    svm_lin.train(100,0.0001)
    w = svm_lin.computW()
    print(w,svm_lin.b)
    showClassifer(x, y,w,svm_lin.b,svm_lin.alpha) 
    """
    X_lin,Y_lin = loadDataSet('testSet.txt')
    svm_lin = SVM(X_lin, Y_lin,'liner')
    #svm_lin = SVM(X_lin, Y_lin,'RBF')#非线性比较通用，虽然所构造的线我不知如何体现
    svm_lin.train(100,0.0001)
    print(svm_lin.predict(X_lin, Y_lin))
    showClassifer(X_lin, Y_lin,svm_lin.computW(),svm_lin.b,svm_lin.alpha)   
    
    X_test,Y_test = loadDataSet('testSetRBF2.txt')
    X_RBF,Y_RBF = loadDataSet('testSetRBF.txt')
    svm_RFB = SVM(X_RBF, Y_RBF,'RBF')
    svm_RFB.train(100,0.0001)
    print(svm_RFB.predict(X_test, Y_test))    
    showDataSet(X_test,Y_test)
    
    """
    pass

if __name__=='__main__':
    main()

看了一些博主的没理解，先放放