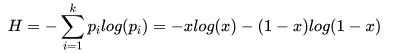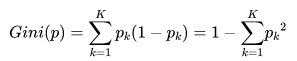【机器学习】（七）——决策树

学习目标：

1、决策树：决策树、信息熵与最优划分、基尼系数、CART

2、实现：决策树实现

学习内容：

【1】

决策树：（decision tree）是一类常见的机器学习方法。它的思想十分朴素，类似于我们平时利用选择做决策的过程。它是类似流程图的结构，其中每个内部节点表示一个测试功能，即类似做出决策的过程（动作），每个叶节点都表示一个类标签，即在计算所有特征之后做出的决定（结果）。标签和分支表示导致这些类标签的功能的连接。从根到叶的路径表示分类规则。

用决策树分类：从根节点开始，对实例的某一特征进行测试，根据测试结果将实例分配到其子节点，此时每个子节点对应着该特征的一个取值，如此递归的对实例进行测试并分配，直到到达叶节点，最后将实例分到叶节点的类中。

信息熵：熵是热力学中的概念，表示混乱程度。熵越大，热力系统中粒子无规则的运动越剧烈；熵越小，粒子越趋近于静止的状态。

  引申到信息论和概率统计中，信息熵表示随机变量的不确定度。对于一组数据来说，越随机、不确定性越高，信息熵越大；不确定性越低，信息熵越小。

  为了计算熵，我们需要计算所有类别所有可能值所包含的信息期望值，著名的香农公式：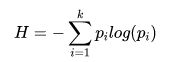

  在一个系统中，有k类的信息， 其中是选择该分类的概率（n/k），再乘p的对数，求和后加上负号。这是因为概率 是小于1的数，是小于0的数，我们要求得到的熵是大于0的。

  如果在二分类的情况下，信息熵公式也可以写为下面的形式：

    

最优划分：

决策树算法的三个步骤：特征选择、决策树生成、决策树剪枝。其中特征选择要解决的核心问题就是：

• 每个节点在哪个维度上做划分？

• 某个维度在哪个值上做划分？

划分的依据是： 要让数据划分成两部分之后，系统整体的信息熵降低。

具体方法是： 对所有的划分可行性进行搜索。下一篇我们模拟在一个节点上进行搜索，找到一个节点上信息熵的最优划分。

基尼系数：（Gini），也被称为基尼不纯度，表示在样本集合中一个随机选中的样本被分错的概率。

  Gini系数越小表示集合中被选中的样本被分错的概率越小，也就是说集合的纯度越高，反之，基尼指数集合越不纯。

  即：基尼指数（基尼不纯度）= 样本被选中的概率 * 样本被分错的概率

  有如下公式：

  

 公式说明：

•  表示选中的样本属于k类别的概率，则这个样本被分错的概率是(1-)

• 因为样本集合中有k个类别，一个随机选中的样本可以属于这k个类别中的任意一个，因而累加所有的k个类别。

• 当二分类时，

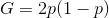
样本集合D的基尼系数：假设集合中有K个类别，每个类别的概率是，其中表示类别k的样本个数，表示样本总数，则：

CART：Classification And Regression Tree。顾名思义，CART算法既可以用于创建分类树（Classification Tree），也可以用于创建回归树（Regression Tree）、模型树（Model Tree），两者在建树的过程稍有差异。既可以解决分类问题，也可以解决回归问题。根据某一个维度d和某一个阈值v进行二分，得到的决策树是二叉树。

  CART分类树算法使用基尼系数来代替信息增益比，基尼系数代表了模型的不纯度，基尼系数越小，不纯度越低，特征越好。这和信息增益（比）相反。

  CART作为分类树时，特征属性可以是连续类型也可以是离散类型，但观察属性(即标签属性或者分类属性)必须是离散类型。

   离散特征：

  CART分类树算法对离散值的处理，采用的思路：不停的二分离散特征。

  在ID3、C4.5，特征A被选取建立决策树节点，如果它有3个类别A1,A2,A3，我们会在决策树上建立一个三叉点，这样决策树是多叉树。

  CART采用的是不停的二分。会考虑把特征A分成{A1}和{A2,A3}、{A2}和{A1,A3}、{A3}和{A1,A2}三种情况，找到基尼系数最小的组合。

  比如{A2}和{A1,A3}，然后建立二叉树节点，一个节点是A2对应的样本，另一个节点是{A1,A3}对应的样本。**由于这次没有把特征A的取值完全分开，各分支下的子数据集必须依旧包含该特征，该连续特征在接下来的树分支过程中可能依旧起着决定性作用。后面还有机会对子节点继续选择特征A划分A1和A3。这和ID3、C4.5不同，在ID3或C4.5的一颗子树中，离散特征只会参与一次节点的建立。

  连续特征：

  CART分类树算法对连续值的处理，思想和C4.5相同，都是将连续的特征离散化。唯一区别在选择划分点时，C4.5是信息增益比，CART是基尼系数。

  具体思路：m个样本的连续特征A有m个，从小到大排列，则CART取相邻两样本值的平均数做划分点，一共取m-1个，其中第i个划分点Ti表示为：。分别计算以这m-1个点作为二元分类点时的基尼系数。选择基尼系数最小的点为该连续特征的二元离散分类点。比如取到的基尼系数最小的点为，则小于的值为类别1，大于的值为类别2，这样就做到了连续特征的离散化。另外，对于连续属性先进行排序（升序），只有在决策属性（即分类发生了变化）发生改变的地方才需要切开，这可以显著减少运算量。

  注意的是，与ID3、C4.5处理离散属性不同的是，如果当前节点为连续属性，则该属性在后面还可以参与子节点的产生选择过程。

  CART分类树算法流程：

 CART分类树建立算法流程，之所以加上建立，是因为CART分类树算法有剪枝。

 算法从根节点开始，用训练集递归建立CART分类树。

输入:训练集D，基尼系数的阈值，样本个数阈值。

输出:决策树T。

1）对于当前节点的数据集为D，如果样本个数小于阈值或没有特征，则返回决策子树，当前节点停止递归。

2）计算样本集D的基尼系数，如果基尼系数小于阈值，则返回决策树子树，当前节点停止递归。

3）计算当前节点现有的各个特征的各个特征值对数据集D的基尼系数。

4）在计算出来的各个特征的各个特征值对数据集D的基尼系数中，选择基尼系数最小的特征A和对应的特征值a。根据这个最优特征和最优特征值，把数据集划分成两部分D1和D2，同时建立当前节点的左右节点，做节点的数据集D为D1，右节点的数据集D为D2。

5）对左右的子节点递归的调用1-4步，生成决策树。算法从根节点开始，用训练集递归建立CART分类树。

  对生成的决策树做预测的时候，假如测试集里的样本A落到了某个叶子节点，而节点里有多个训练样本。则对于A的类别预测采用的是这个叶子节点里概率最大的类别。

 

【2】

# 数据引入及可视化
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

iris = datasets.load_iris()
X = iris.data[:,2:] # iris有四个特征，这里取后两个，形成一个坐标点
y = iris.target
# 绘图
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.scatter(X[y==2,0],X[y==2,1])
plt.show()

# 进行分类
from sklearn.tree import DecisionTreeClassifier
# 创建决策树对象，最大深度max_depth为2层，criterion评判标准为entropy（熵）
dt_clt = DecisionTreeClassifier(max_depth=2,criterion='entropy')
# 将训练数据送给模型
dt_clt.fit(X,y)

# 绘制决策边界
def plot_decision_boundary(model, axis): # model是模型，axis是范围
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1),
        np.linspace(axis[2], axis[3],int((axis[3]-axis[2])*100)).reshape(-1,1),
    )
    X_new = np.c_[x0.ravel(), x1.ravel()]

    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)

    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    
    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)

# 数据可视化    
plot_decision_boundary(dt_clt, axis=[0.5,7.5,0,3])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.scatter(X[y==2,0],X[y==2,1])
plt.show()