序列模式
什么是序列模式
Apriori处理的数据没有考虑每个客户在超市多次购物的情况。
序列模式:一个用户在不同时间点的交易记录就构成了一个购买序列,
N个用户的购买序列就组成一个规模为N的序列数据集.。
Apriori目的:挖掘出频繁集,找到其中的关联规则
对于Apriori处理的数据集设置支持度阈值为:2
则(面包机、面包)为频繁集
设置可信度为:0.7
则关联规则:面包机 ——> 面包
这条关联规则的意义:在一次交易中买了面包机,就很可能买面
序列模式目的:挖掘满足最小支持度的频繁序列
对于序列模式处理的数据集设置支持度阈值为:2
则<面包机 面包> 为频繁序列
这条频繁序列的意义:如果一个顾客买了面包机,那么他以后就回来买面包
如果我来经营一家超市,通过Apriori算法,我需要将面包机与面包放在一起,通过序列模式,我知道如果一段时间内面包机卖了很多,我将多进货面包
序列模式三个算法GSP SPADE PrifixSpan
GSP

举例:

设置支持度阈值为:3

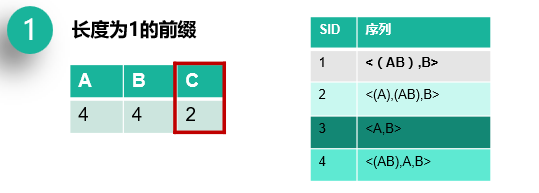
(1)扫描序列数据库,对每一项进行支持度统计,得到长度为1的频繁序列模式
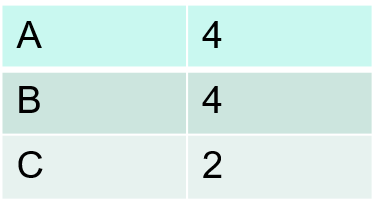

(2)根据长度为1的频繁序列,通过连接操作生成长度为2的候选序列模式,然后扫描序列数据库,计算每个候选序列的支持度,通过删除操作产生长度为2的频繁序列模式
![]()
(3)根据长度为2的频繁序列,通过连接操作生成长度为3的候选序列模式,然后扫描序列数据库,计算每个候选序列的支持度,通过删除操作产生长度为3的频繁序列模式

这里没有统计
没有统计
SPADE
SPADE算法是Zaki在2001年发表的《An efficient algorithm for mining frequent sequences》提出的。
SPADE的算法过程和GSP类似,只是在扫描的时候不是扫描整个数据库,而是扫描ID_LIST.
举例:
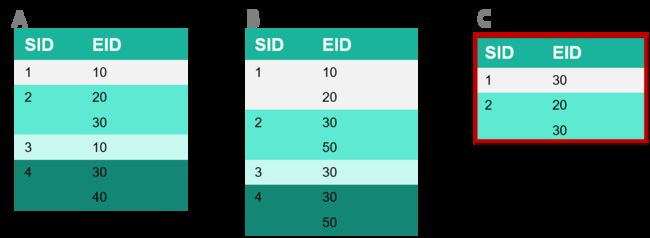
红色框代表非频繁序列
2序列的ID_list
注意:
3序列的ID_list
注意:
SPADE:通过便利一次数据库得到的经验知识来降低多次对数据库的扫描。
SPADE不仅通过减少对数据库的扫描降低I/O成本通过搜索ID_list降低计算成本。
PrefixSpan

设置支持度阈值为:3
(1)对数据库中所有的项进行支持度统计,将支持度低于阈值的项从数据库中删除,得到长度为1的前缀
注意:
B和_B不一样,前者是前缀A与B在不同的项集,后者是和前缀A在相同的项集中。
a,b,c 分别对应PrefixSpan算法步骤第二步中的a,b,c
(3)重复第二步
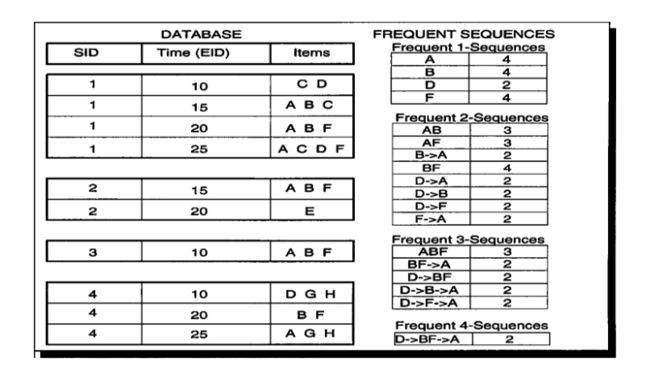
GSP实验
数据集采用的是Zaki在2001年发表的《An efficient algorithm for mining frequent sequences》中的一个例子。#coding=utf-8
import itertools
import sys
import datetime
#-----------------
class GSP(object):
def __init__(self):
self.queue = []
#----------------------------------------------------------#
# 计算freq1 #
#----------------------------------------------------------#
def freq1(self, data, frequent_num):
appear = ''
freq1 = []
appear_ele = []
appear_ele2 = []
for i in range(len(data)):
appear = ''
for j in range(len(data[i])):
appear += data[i][j]
appear_ele += list(set(appear))
# print(appear_ele)
appear_ele2 = list(set(appear_ele))
# print(appear_ele2)
for item in appear_ele2:
itmes = appear_ele.count(item)
if itmes >= frequent_num:
freq1.append(item)
print('频繁1项集为:%s' %freq1)
return freq1
#----------------------------------------------------------#
# 计算freq_more #
#----------------------------------------------------------#
def freq_more(self, data, freq1):
queue = []#所有的备选序列放在这里面
queue_new = []#最终结果在这里面
top = 0 #这个是queue_new的队尾标号
times = 3
while True:
if (queue_new == []): #为空则代表这是第一次遍历,python中的&&是and,||是or
for i in range(len(freq1)):
for j in range(i+1, len(freq1)):
item = freq1[i] + freq1[j]
queue.append(item)
for i in range(len(freq1)):
for j in range(len(freq1)):
if j != i:
item = freq1[i] +'->'+ freq1[j]
queue.append(item)#第一次遍历后全部可能出现的情况
for i in range(len(queue)):
freq_item = self.isFreq(queue[i], data)
if freq_item != 0:
queue_new.append(freq_item)
queue = []#清空queue(备选序列)
if (queue_new != []): #后几次遍历时要把所有的情况写入空的queue中
if top == len(queue_new) - 1: #表示没有新加入元素,那么终止 while 循环
print('频繁多项集为:%s' %queue_new)
break
else:
demo_list = []#专门放'AB','BF','AF'这样的频繁序列,后面将他们合成为更多成员的备选频繁序列
for i in range(top, len(queue_new)):
if '->' not in queue_new[i]:
demo_list.append(queue_new[i])
demo_string = self.List_to_String(demo_list) #将列表中的元素拼接成字符串,诸如拼成'ABBFAF'
demo_ele = "".join(set(demo_string)) #删除串中的重复元素,输出'ABF'
if len(demo_ele) >= times:
if len(demo_ele) == times :#那么demo_ele是唯一的备选成员
queue.append(demo_ele)
times += 1
else: #否则对备选字母进行排列组合,比如'ABCDE',一共能排列出10钟情况,并把它们推入queue(待判断成员队列)
combin = self.Combinations(demo_ele, times)
for i in range(len(combin)):
queue.append(combin[i])
times += 1
###-----####至此已经把备选频繁寻列推入 queue ####-----###
queue = self.Make_time_queue(top, freq1, queue, queue_new)
###-----#### 至此已经把 queue 放满了备选成员 ####-----###
top = len(queue_new)# 更新队尾指针 top 的位置
###-----#### 检测 queue 中的备选序列是否频繁 ####-----###
for i in range(len(queue)):
freq_item = self.isFreq(queue[i], data) #---->> isFreq
if freq_item != 0: #如果这个成员是频繁的
queue_new.append(freq_item)
queue = []
#将列表中的字母合并成字符串
def List_to_String(self, list):
demo_string = ''
for i in range(len(list)):
demo_string = demo_string + list[i]
return demo_string
#demo_ele是待排列的字符串, times是将它们排列成几个元素
def Combinations(self, item, times):
demo_list = []
combin = []
element = ''
for i in range(1, len(item) +1):
iter = itertools.combinations(item, i)
demo_list.append(list(iter))
demo_combin = demo_list[times -1]
for i in range(len(demo_combin)):
for j in range(len(demo_combin[0])):
element += demo_combin[i][j]
combin.append(element)
element = ''
return combin
#判断item是不是频繁的
def isFreq(self, item, data):
num = 0
if '->' not in item: #类似如'ABF'
for i in range(len(data)):
for j in range(len(data[i])):
if self.isIn_Item(item, data, i, j) != 0:
num += 1
if num >= 2:
return item
else:
return 0
else: #类似如‘D->B->A’
item0 = item.split('->')
for i in range(len(data)):
array = 0
j = 0
while True:
if array == len(item0) or j == len(data[i]):
break
if len(item0[array]) >= 2: #如果类似 'BA' 形式
if self.isIn_Item(item0[array], data, i, j) == 1:
array += 1
j += 1
else:
j += 1
else:
if item0[array] in data[i][j]:
array += 1
j += 1
else:
j += 1
if array == len(item0):
num += 1
if num >= 2:
return item
else:
return 0
#判断 item 是否在 data[i][j]中
def isIn_Item(self, item, data, i, j):
demo_num = 0
for k in range(len(item)):
if item[k] in data[i][j]:
demo_num += 1
if demo_num == len(item):
return 1
else:
return 0
#
def isIn_Time(self, item0, data, i, j):
num = 0
item0_lenth = len(item0)
if item0_lenth == 2:
for m in range(j+1, len(data[i])):
if item0[1] in data[i][m]:
num += 1
else:
if item0[item0_lenth -2] in data[i][j]:
for m in range(j+1, len(data[i])):
if item0[item0_lenth -1] in data[i][m]:
num += 1
break
return num
#创造新的备选时间序列
def Make_time_queue(self, top, freq1, queue, queue_new):
for i in range(top, len(queue_new)):
# for j in range(len(freq1)):
if '->' not in queue_new[i]:
difference = self.Difference(queue_new[i], freq1)
for j in range(len(difference)):
queue.append(difference[j] + '->' +queue_new[i]) #诸如 'D->AB'
queue.append(queue_new[i] + '->' +difference[j]) #诸如 'AB->D'
else:
difference = self.Difference(queue_new[i], freq1)
for j in range(len(difference)):
queue.append(queue_new[i] + '->' + difference[j]) #诸如'B->A' 扩展成 'B->A->D'
return queue
#寻找两个字符串中的不同字母,并提取出来
def Difference(self, item, freq1):
demo_list = []
if '->' not in item:
for i in range(len(freq1)):
if freq1[i] not in item:
demo_list.append(freq1[i])
else:
demo_item = item.split('->') #将诸如'A->B'拆分成 'A','B'
demo_item_string = self.List_to_String(demo_item) #合并成'AB'
for i in range(len(freq1)):
if freq1[i] not in demo_item_string:
demo_list.append(freq1[i])
return demo_list
# main #
#----------------------------------------------------------#
data = {0:['CD','ABC','ABF','ACDF'],
1:['ABF','E'],
2:['ABF'],
3:['DGH','BF','AGH']}
starttime = datetime.datetime.now()
g= GSP()
freq1 = g.freq1(data,2)
g.freq_more(data, freq1)
endtime = datetime.datetime.now()
print(endtime - starttime)
问题:
序列模式挖掘出频繁序列假设为