关于TensorFlow的卷积函数conv2d的参数解释
一、卷积操作原理
卷积运算
虽然卷积层得名于卷积(convolution)运算,但我们通常在卷积层中使用更加直观的互相关(cross-correlation)运算。在二维卷积层中,一个二维输入数组和一个二维核(kernel)数组通过互相关运算输出一个二维数组。 我们用一个具体例子来解释二维互相关运算的含义。如图5.1所示,输入是一个高和宽均为3的二维数组。我们将该数组的形状记为 3×3 或(3,3)。核数组的高和宽分别为2。该数组在卷积计算中又称卷积核或过滤器(filter)。卷积核窗口(又称卷积窗口)的形状取决于卷积核的高和宽,即 2×2 。图5.1中的阴影部分为第一个输出元素及其计算所使用的输入和核数组元素: 0×0+1×1+3×2+4×3=19

填充和步幅
在上一节的例子里,我们使用高和宽为3的输入与高和宽为2的卷积核得到高和宽为2的输出。一般来说,假设输入形状是 nh×nw ,卷积核窗口形状是 kh×kw ,那么输出形状将会是
(nh−kh+1)×(nw−kw+1).
所以卷积层的输出形状由输入形状和卷积核窗口形状决定。本节我们将介绍卷积层的两个超参数,即填充和步幅。它们可以对给定形状的输入和卷积核改变输出形状。

一般来说,如果在高的两侧一共填充 ph 行,在宽的两侧一共填充 pw 列,那么输出形状将会是
(nh−kh+ph+1)×(nw−kw+pw+1),
也就是说,输出的高和宽会分别增加 ph 和 pw 。
在很多情况下,我们会设置 ph=kh−1 和 pw=kw−1 来使输入和输出具有相同的高和宽。这样会方便在构造网络时推测每个层的输出形状。假设这里 kh 是奇数,我们会在高的两侧分别填充 ph/2 行。如果 kh 是偶数,一种可能是在输入的顶端一侧填充 ⌈ph/2⌉ 行,而在底端一侧填充 ⌊ph/2⌋ 行。在宽的两侧填充同理。
卷积神经网络经常使用奇数高宽的卷积核,如1、3、5和7,所以两端上的填充个数相等。对任意的二维数组X,设它的第i行第j列的元素为X[i,j]。当两端上的填充个数相等,并使输入和输出具有相同的高和宽时,我们就知道输出Y[i,j]是由输入以X[i,j]为中心的窗口同卷积核进行互相关计算得到的。
多输入通道和多输出通道
前面两节里我们用到的输入和输出都是二维数组,但真实数据的维度经常更高。例如,彩色图像在高和宽2个维度外还有RGB(红、绿、蓝)3个颜色通道。假设彩色图像的高和宽分别是 h 和 w (像素),那么它可以表示为一个 3×h×w 的多维数组。我们将大小为3的这一维称为通道(channel)维。本节我们将介绍含多个输入通道或多个输出通道的卷积核。
当输入数据含多个通道时,我们需要构造一个输入通道数与输入数据的通道数相同的卷积核,从而能够与含多通道的输入数据做互相关运算。假设输入数据的通道数为 ci ,那么卷积核的输入通道数同样为 ci 。设卷积核窗口形状为 kh×kw 。当 ci=1 时,我们知道卷积核只包含一个形状为 kh×kw 的二维数组。当 ci>1 时,我们将会为每个输入通道各分配一个形状为 kh×kw 的核数组。把这 ci 个数组在输入通道维上连结,即得到一个形状为 ci×kh×kw 的卷积核。由于输入和卷积核各有 ci 个通道,我们可以在各个通道上对输入的二维数组和卷积核的二维核数组做互相关运算,再将这 ci 个互相关运算的二维输出按通道相加,得到一个二维数组。这就是含多个通道的输入数据与多输入通道的卷积核做二维互相关运算的输出。
图5.4展示了含2个输入通道的二维互相关计算的例子。在每个通道上,二维输入数组与二维核数组做互相关运算,再按通道相加即得到输出。图5.4中阴影部分为第一个输出元素及其计算所使用的输入和核数组元素: (1×1+2×2+4×3+5×4)+(0×0+1×1+3×2+4×3)=56 。

二、conv2d()函数
TensorFlow中的函数声明和python API
tf.nn.conv2d(
input,
filter,
strides,
padding,
use_cudnn_on_gpu=True,
data_format='NHWC',
dilations=[1, 1, 1, 1],
name=None
)
-
input: A Tensor. Must be one of the following types: half, bfloat16,
float32, float64. A 4-D tensor. The dimension order is interpreted
according to the value of data_format, see below for details. -
filter: A Tensor. Must have the same type as input. A 4-D tensor of
shape [filter_height, filter_width, in_channels, out_channels] -
strides: A list of ints. 1-D tensor of length 4. The stride of the
sliding window for each dimension of input. The dimension order is
determined by the value of data_format, see below for details. -
padding: A string from: “SAME”, “VALID”. The type of padding
algorithm to use. -
use_cudnn_on_gpu: An optional bool. Defaults to True.
-
data_format: An optional string from: “NHWC”, “NCHW”. Defaults to
“NHWC”. Specify the data format of the input and output data. With
the default format “NHWC”, the data is stored in the order of:
[batch, height, width, channels]. Alternatively, the format could be
“NCHW”, the data storage order of: [batch, channels, height, width]. -
dilations: An optional list of ints. Defaults to [1, 1, 1, 1]. 1-D
tensor of length 4. The dilation factor for each dimension of input.
If set to k > 1, there will be k-1 skipped cells between each filter
element on that dimension. The dimension order is determined by the value of data_format, see above for details. Dilations in the batch
and depth dimensions must be 1. -
name: A name for the operation (optional).
主要讲解前四个参数:
在默认data_format=“NHWC”时,
4D张量的格式为[batch, height, width, channels],以图片处理为例:分别为图片的批量(每次处理的图片张数),图片高度像素数,图片宽度的像素数,图片通道数(彩色为3通道,灰度为一通道,其余可能还有深度等)
此时
input的四个参数分别为输入张量的上述参数
filter的四个参数[filter_height, filter_width, in_channels, out_channels],分别为卷积核/滤波器的像素高度,像素宽度,输入通道数(与input中的通道数相等),输出通道数(卷积核个数,卷积层学习的特征个数)
注意:一个卷积核可能有多个通道,其通道数与输入的张量通道数相同。
strides:四维张量,[----,高度步长,宽度步长,----],第一和第四个数没用,但是默认为1
padding:填充方式:
“SAME”:用0填充边缘,使得卷积后的图像尺寸和原始图像一致,
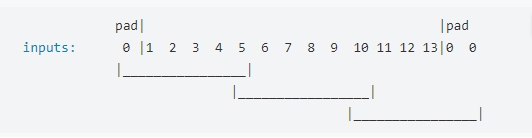
“VALID”:不填充,右边和下边多余的行和列丢弃
