数据结构和算法——排序算法(2)——基于比较的O(n^2)的排序算法(2)——选择排序、插入排序
目录
1.选择排序
1.1 基本思想
1.2 图解原理:
1.3 Java代码实现
1.4 性能分析
2.插入排序
2.1 基本思想
2.2 图解原理
2.3 代码实现
2.4 优化——折半插入排序
2.5 性能测试
(1)直接插入排序和选择排序性能测试代码:(输入数据为随机数据)
(2)直接插入排序和折半插入排序性能测试代码:(输入数据为随机数据)
3.三种基于比较的O(n^2)的排序算法总结
分享一个超级好的理解算法的网站(会以动画的形式显示每一步执行结果):https://visualgo.net/en
1.选择排序
1.1 基本思想
- 第一次从arr[0]~arr[n-1]中选取最小值,与arr[0]交换,
- 第二次从arr[1]~arr[n-1]中选取最小值,与arr[1]交换
- ......
- 第i次从arr[i-1]~arr[n-1]中选取最小值,与arr[i-1]交换
- ......
- 第n-1次从arr[n-2]~arr[n-1]中选取最小值,与arr[n-2]交换
- 总共通过n-1次,得到一个从小到大排列的有序序列
- 之所以叫选择排序,是因为它在不断地选择剩余元素之中的最小者
1.2 图解原理:
小结:
- 一共进行n-1次排序(n为数组的长度)
- 冒泡排序是从未排序的数组中把最大值交换到未排序的最右边,而选择排序是每次从未排序的序列中选出最小值放置在未排序的最左边
- 每次排序都要进行一次交换,每次交换都能确定一个元素,所以算法的时间效率取决于比较的次数
1.3 Java代码实现
import java.util.Arrays;
public class SelectionSort extends Sort{
@Override
public void sort(Comparable[] arr) {
int min = 0; //用来存放每一趟的最小值
//外部循环为排序次数
for (int i = 0; i < arr.length-1; i++)
{
min = i;
//每一趟将未排序的数组遍历比较每个元素与最小值来找出最小值所在位置的索引
for (int j = i; j < arr.length; j++) //这里不存在访问j+1的情况,而是要将数组访问完
{
//如果当前位置小于最小值,则更新最小值
if (arr[j].compareTo(arr[min]) < 0)
min = j;
//否则就继续迭代下一个位置
}
//每一趟结束找到最小值后,将最小值与未排序的第一个元素做交换
swap(arr, i,min);
//以下两步不是必须,此处打印只是为了结果能清楚的观察
System.out.println("第"+(i+1)+"趟排序后的数组为:");
System.out.println(Arrays.toString(arr));
}
}
}
import java.util.Arrays;
public class SortTest {
public static void main(String[] args) {
Integer[] arr = new Integer[]{3, 9, -1, 10, -2};
System.out.println("未排序前的数组为:");
System.out.println(Arrays.toString(arr));
SelectionSort selectionSort = new SelectionSort();
selectionSort.sort(arr);
}
}
1.4 性能分析
- 运行时间与输入无关,即与输入的数组是否排序无关
- 选择排序的数据移动是最少的,每次交换都会改变两个数组元素的值,因此选择排序用了n-1次交换,交换次数和数组的大小是线性关系,其他任何算法都不具备这个特征
- 遍历次数:n-1(n为数组长度)
- 比较次数:

- 交换次数:n-1
优化前的冒泡排序和选择排序性能测试代码:
public class SortPerformanceTest {
public static void main(String[] args) {
//创建100000个随机数据
Double[] arr1 = new Double[100000];
for (int i = 0; i < arr1.length; i++) {
arr1[i] = (Double) (Math.random() * 10000000); //这里使用10000000是为了让数据更分散
}
//赋值上述创建的数组arr1的值到数组arr2
Double[] arr2 = new Double[100000];
for (int i = 0; i < arr1.length; i++) {
arr2[i] = arr1[i];
}
//创建两种排序类的对象
BubbleSort bubbleSort = new BubbleSort();
SelectionSort selectionSort = new SelectionSort();
//使用优化前的冒泡排序对arr1进行排序
long bubbleSort_start = System.currentTimeMillis();
bubbleSort.sort(arr1);
long bubbleSort_end = System.currentTimeMillis();
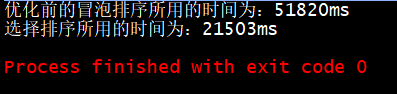
System.out.println("优化前的冒泡排序所用的时间为:"+(bubbleSort_end - bubbleSort_start)+"ms");
//使用选择排序对arr2进行排序
long selectionSort_start = System.currentTimeMillis();
selectionSort.sort(arr2);
long selectionSort_end = System.currentTimeMillis();
System.out.println("选择排序所用的时间为:"+(selectionSort_end - selectionSort_start)+"ms");
}
}
可以发现,选择排序要比未优化的冒泡排序要快一些,它们的遍历次数和比较次数相同的,但是大多数情况选择排序的交换次数比冒泡排序要少
2.插入排序
2.1 基本思想
- 把n个待排序的元素看成为一个有序表和一个无序表,开始时有序表中只包含第一个元素,无序表中包含n-1个元素,
- 排序过程中每次从无序表中取出第一个元素,把它的值依次与有序表元素的排序码进行比较,将它插入到有序表中的适当位置,使之成为新的有序表
- 直到无序表为空为止,即所有元素都在有序表中排好顺序
2.2 图解原理
- 插入的次数为n-1,即将无序表中n-1个值插入到有序表中
2.3 代码实现
(1)通过交换元素实现的直接插入排序
import java.util.Arrays;
public class DirectInsertionSort_Swap extends Sort{
@Override
public void sort(Comparable[] arr) {
//第一种写法
// 保存插入值的位置
// 比较该插入值和它前面的值,小于就交换(顺便就发生了元素的移动),大于等于就插入成功
//外层循环为插入的次数
//默认第一个元素是有序的
for (int i = 1; i < arr.length; i++) {
//定义一个临时变量保存插入值的位置,因为插入值的位置会随着交换而变化,我们需要记录
int insertValuePos = i;
//内层循环为将无序表中第一个元素从后向前遍历有序表比较进行插入
for (int j = i-1; j >= 0; j--) {
//要插入的元素小于正在遍历的元素
if(arr[insertValuePos].compareTo(arr[j]) < 0){
//小于就交换
swap(arr,insertValuePos,j);
//并且此时原来要插入的值的位置发生了变化
insertValuePos--;
}else{
//如果没有发生交换,表明已经插入到了合适的位置
break;
}
}
System.out.println("第"+i+"轮插入后数组为:");
System.out.println(Arrays.toString(arr));
}
}
}
import java.util.Arrays;
public class SortTest {
public static void main(String[] args) {
Integer[] arr = new Integer[]{3, -1, 10, 9, -2};
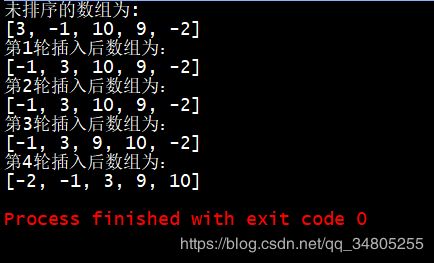
System.out.println("未排序的数组为:");
System.out.println(Arrays.toString(arr));
DirectInsertionSort_Swap directInsertionSort_swap = new DirectInsertionSort_Swap();
directInsertionSort_swap.sort(arr);
}
}
(2)通过移动元素实现的直接插入排序
import java.util.Arrays;
public class DirectInsertionSort_Move extends Sort{
@Override
public void sort(Comparable[] arr) {
//第二种写法:
// 先保存插入元素,找到它要插入的位置,
// 移动该位置后的所有元素(有序序列中),最后将保存的值插入该位置
//外层循环为插入的次数
//默认第一个元素是有序的
for (int i = 1; i < arr.length; i++) {
//保存要插入的元素的值
Comparable insertVal = arr[i];
//从要插入的元素的前一个位置开始寻找当前要插入元素的位置,并将它后面的元素后移
int j = i-1;
for (; j >= 0; j--) {
//插入值小于当前遍历元素
if(insertVal.compareTo(arr[j]) < 0){
//当前元素右移
arr[j+1] = arr[j];
}else {
//插入值大于等于当前遍历元素,结束比较
break;
}
}
//通过上述移动,最后确定j+1为插入的位置,进行插入
arr[j+1] = insertVal;
System.out.println("第"+i+"轮插入后数组为:");
System.out.println(Arrays.toString(arr));
}
}
}
import java.util.Arrays;
public class SortTest {
public static void main(String[] args) {
Integer[] arr = new Integer[]{3, -1, 10, 9, -2};
System.out.println("未排序的数组为:");
System.out.println(Arrays.toString(arr));
DirectInsertionSort_Move directInsertionSort_move = new DirectInsertionSort_Move();
directInsertionSort_move.sort(arr);
}
}
(3)上述两种实现方式性能比较
public class SortPerformanceTest {
public static void main(String[] args) {
//创建100000个随机数据
Double[] arr1 = new Double[100000];
for (int i = 0; i < arr1.length; i++) {
arr1[i] = (Double) (Math.random() * 10000000); //这里使用10000000是为了让数据更分散
}
//赋值上述创建的数组arr1的值到数组arr2
Double[] arr2 = new Double[100000];
for (int i = 0; i < arr1.length; i++) {
arr2[i] = arr1[i];
}
//创建两种排序类的对象
DirectInsertionSort_Swap directInsertionSort_swap = new DirectInsertionSort_Swap();
DirectInsertionSort_Move directInsertionSort_move = new DirectInsertionSort_Move();
//使用交换实现的直接插入排序对arr1进行排序
long swap_start = System.currentTimeMillis();
directInsertionSort_swap.sort(arr1);
long swap_end = System.currentTimeMillis();
System.out.println("使用交换实现的直接插入排序所用的时间为:"+(swap_end - swap_start)+"ms");
//使用移动元素实现的直接插入排序对arr2进行排序
long move_start = System.currentTimeMillis();
directInsertionSort_move.sort(arr2);
long move_end = System.currentTimeMillis();
System.out.println("使用移动元素实现的直接插入排序所用的时间为:"+(move_end - move_start)+"ms");
}
}
可以发现使用移动元素来实现比交换的性能高,所以我们应该第二种方式来实现插入排序,即:
- 1.保存插入元素
- 2.找到插入位置
- 3.将插入位置及以后的元素右移一位
- 4.插入该元素
2.4 优化——折半插入排序
- 我们可以看到每次插入,我们都是向一个有序的序列当中插入元素,那么我们可以利用这个有序,来缩短它的比较次数,
- 每次都要从有序序列中查找插入位置,有序序列——查找,我们可以立马想到二分查找算法,
- 我们可以在搜索位置的时候利用二分查找来缩短比较次数
实现代码:
import java.util.Arrays;
public class HalfInsertionSort extends Sort{
@Override
public void sort(Comparable[] arr) {
//外层循环为插入的次数
//默认第一个元素是有序的
for (int i = 1; i < arr.length; i++) {
//保存要插入的元素的值
Comparable insertVal = arr[i];
//通过折半查找寻找要插入的位置
int left = 0;
int right = i-1;
/**
* 结束循环的前一步:
* left+1=right,此时循环,middle=left,
* 此时执行if的话,left便和right相等,此时循环,middle = left = right,
* 此时执行if表示要插入的值大于arr[middle],此时执行后left = right + 1,
* 如果执行else表示要插入的值小于arr[middle],此时执行后left = right + 1
* 执行else,left = right + 1
*
* 综上:下述写法最终left = right + 1
* 这样下来就确定了left是最终的插入位置,
* 因为最终的left = right最后一次移动之前的middle,大于left最后一次移动之前的middle,
* 所以最终的位置在这两个值中间插入,所以只需要将left及其之后的元素右移即可
*/
while(left <= right){
int middle = (left + right)/2;
if(insertVal.compareTo(arr[middle]) > 0){
left = middle + 1;
}else {
right = middle - 1;
}
}
//将从left开始的所有数据右移1位
for (int j = i-1; j >= left; j--) {
arr[j+1] = arr[j];
}
//将
arr[left] = insertVal;
System.out.println("第"+i+"轮插入后数组为:");
System.out.println(Arrays.toString(arr));
}
}
}
折半查找只是减少了比较次数,但是元素的移动次数不变,所以时间复杂度仍然为O(n^2)
2.5 性能测试
- 运行时间与输入有关,即运行时间取决于输入中元素的初始顺序
- 数据有序程度越高,越高效
- 插入排序也很适合小规模数组
- 时间复杂度:O(n^2)
- 空间复杂度:O(1)
- 遍历次数:n-1(n为数组长度)
- 比较次数:
- 交换次数:
(1)直接插入排序和选择排序性能测试代码:(输入数据为随机数据)
public class SortPerformanceTest {
public static void main(String[] args) {
//创建100000个随机数据
Double[] arr1 = new Double[100000];
for (int i = 0; i < arr1.length; i++) {
arr1[i] = (Double) (Math.random() * 10000000); //这里使用10000000是为了让数据更分散
}
//赋值上述创建的数组arr1的值到数组arr2
Double[] arr2 = new Double[100000];
for (int i = 0; i < arr1.length; i++) {
arr2[i] = arr1[i];
}
//创建两种排序类的对象
DirectInsertionSort_Move directInsertionSort = new DirectInsertionSort_Move();
SelectionSort selectionSort = new SelectionSort();
//使用直接插入排序对arr1进行排序
long directInsertionSort_start = System.currentTimeMillis();
directInsertionSort.sort(arr1);
long directInsertionSort_end = System.currentTimeMillis();
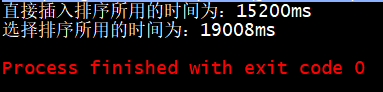
System.out.println("直接插入排序所用的时间为:"+(directInsertionSort_end - directInsertionSort_start)+"ms");
//使用选择排序对arr2进行排序
long selectionSort_start = System.currentTimeMillis();
selectionSort.sort(arr2);
long selectionSort_end = System.currentTimeMillis();
System.out.println("选择排序所用的时间为:"+(selectionSort_end - selectionSort_start)+"ms");
}
}
可以发现对随机排序的无重复主键的数组,插入排序比选择排序快一个较小的常数倍
但对于主键有重复或是排列不随机的情况,上述结论就不一定适用
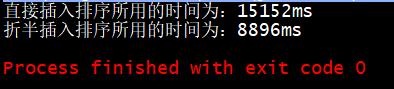
(2)直接插入排序和折半插入排序性能测试代码:(输入数据为随机数据)
public class SortPerformanceTest {
public static void main(String[] args) {
//创建100000个随机数据
Double[] arr1 = new Double[100000];
for (int i = 0; i < arr1.length; i++) {
arr1[i] = (Double) (Math.random() * 10000000); //这里使用10000000是为了让数据更分散
}
//赋值上述创建的数组arr1的值到数组arr2
Double[] arr2 = new Double[100000];
for (int i = 0; i < arr1.length; i++) {
arr2[i] = arr1[i];
}
//创建两种排序类的对象
DirectInsertionSort_Move directInsertionSort = new DirectInsertionSort_Move();
HalfInsertionSort halfInsertionSort = new HalfInsertionSort();
//使用直接插入排序对arr1进行排序
long directInsertionSort_start = System.currentTimeMillis();
directInsertionSort.sort(arr1);
long directInsertionSort_end = System.currentTimeMillis();
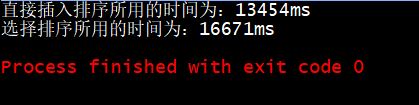
System.out.println("直接插入排序所用的时间为:"+(directInsertionSort_end - directInsertionSort_start)+"ms");
//使用折半插入排序对arr2进行排序
long halfInsertionSort_start = System.currentTimeMillis();
halfInsertionSort.sort(arr2);
long halfInsertionSort_end = System.currentTimeMillis();
System.out.println("折半插入排序所用的时间为:"+(halfInsertionSort_end - halfInsertionSort_start)+"ms");
}
}
可以看到通过折半查找位置来优化插入排序效果还是很明显
3.三种基于比较的O(n^2)的排序算法总结
| 最好情况 | 平均情况 | 最差情况 | ||||
| 排序算法 | 比较次数 | 交换次数 | 比较次数 | 交换次数 | 比较次数 | 交换次数 |
| 冒泡排序 | ||||||
| 选择排序 | ||||||
| 插入排序 | ||||||