tensorflow实战之二：MNIST手写数字识别的优化1-代价函数优化

     上一节我们介绍了最简单的tensorflow的手写识别模型，这一节我们将会介绍其简单的优化模型。我们会从代价函数，多层感知器，防止过拟合，以及优化器的等几个方面来介绍优化过程。

   1.代价函数的优化：

            我们可以这样将代价函数理解为真实值与预测值的差距，我们神经网络训练的目的就是调整W,b等参数来让这个代价函数的值最小。上一节我们用到的是二次代价函数：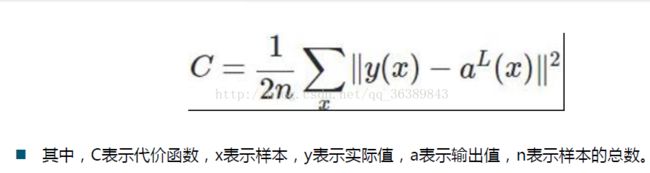

在TensorFlow中的实现为：loss = tf.reduce_mean(tf.square(y-prediction))，但是这个代价函数会带来一定的问题，比如说刚开始学习的会很慢。我们知道神经网络的学习是通过梯度的反向传播来更新参数W,b的：

但是我们的sigmoid激活函数为：

当z很大的时候，例如在B点时，σ'(z)即改点切线的斜率将会很小，导致W,b的梯度很小，神经网络更新的将会很慢。为了解决这个问题，这一节我们将会引入交叉熵代价函数：

其中C为代价函数，x为样本，y为实际值，a为预测值，n为样本总数。

 我们先来观察一下这个代价函数:

当实际值y=1时，C= -1/n *∑ylna,    此时当a->1时，C->0    ,当a->0时C->无穷大

当实际值y=0时，C=-1/n *∑ln(1-a)  此时当a->1时，C->无穷大  ,当a->0时C->0

可以发现当预测值a=实际值y时，这个代价函数将会最小。

接下来我们对其求梯度得：

可以发现其对于W,b的梯度是与σ'(z)无关的，不会因为Z过大引起学习过慢的问题，而且我们发现W,b的梯度与σ(z)-y有关，而这个差值就是预测值与真实值的差值，也就是说当预测值与真实值的偏差很大时，神经网络的更新会很快，当预测值与真实值的偏差很小时，神经网络的更新会减慢，这恰恰符合了我们神经网络的更新策略。因此我们将会用

交叉熵代价函数来代替二次代价函数。也就是会用loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y,logits=prediction))代替之前的loss = tf.reduce_mean(tf.square(y-prediction))。其代码如下：

# coding: utf-8
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data

mnist = input_data.read_data_sets("MNIST_data",one_hot=True)

#每个批次的大小
batch_size = 100
#计算一共有多少个批次
n_batch = mnist.train.num_examples // batch_size

#定义两个placeholder
x = tf.placeholder(tf.float32,[None,784])
y = tf.placeholder(tf.float32,[None,10])

#创建一个简单的神经网络
W = tf.Variable(tf.zeros([784,10]))
b = tf.Variable(tf.zeros([10]))
prediction = tf.nn.softmax(tf.matmul(x,W)+b)

#二次代价函数
# loss = tf.reduce_mean(tf.square(y-prediction))
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y,logits=prediction))
#使用梯度下降法
train_step = tf.train.GradientDescentOptimizer(0.2).minimize(loss)

#初始化变量
init = tf.global_variables_initializer()

#结果存放在一个布尔型列表中
correct_prediction = tf.equal(tf.argmax(y,1),tf.argmax(prediction,1))#argmax返回一维张量中最大的值所在的位置
#求准确率
accuracy = tf.reduce_mean(tf.cast(correct_prediction,tf.float32))

with tf.Session() as sess:
    sess.run(init)
    for epoch in range(21):
        for batch in range(n_batch):
            batch_xs,batch_ys =  mnist.train.next_batch(batch_size)
            sess.run(train_step,feed_dict={x:batch_xs,y:batch_ys})
        
        acc = sess.run(accuracy,feed_dict={x:mnist.test.images,y:mnist.test.labels})
        print("Iter " + str(epoch) + ",Testing Accuracy " + str(acc))

运行结果如下：

上一章的运行结果：

可以发现应用交叉熵代价函数后训练的速率明显加快，在第三轮就达到了90%，而之前的却在第6轮达到90%。

我们可以有这样的结论：如果输出神经元是 线性的，那么二次代价函数就一种合适选择。如果神经元是S型函数的话，那么比较适合用交叉熵代价函数。