BFS广度优先遍历寻找最短路径(超详细实现过程)

广度优先遍历寻找最短路径

      最近一直想搞A*算法，发现有部分没理解清楚。于是找到了广度优先遍历寻路算法学习了下，想看看可不可以对写A*有什么帮助。广度优先遍历寻路算法本身并不难，概括来说就是像雷达一样，一层一层进行寻找目标点。当找到目标点后进行回溯。从而找到最佳路径。也就是说每走一步都要找到到达该点的最短的路径，最终得到到达所有点的最短路径。

废话不多说上代码。具体解释在代码后面

Point.java

public class Point {
	private int x;
	private int y;
	public int getX() {
		return x;
	}
	public void setX(int x) {
		this.x = x;
	}
	public int getY() {
		return y;
	}
	public void setY(int y) {
		this.y = y;
	}
	public Point(int x, int y) {
		super();
		this.x = x;
		this.y = y;
	}
	
}

MyMap.java

public class MyMap {
	//记录上一个父亲位置
	private int preX;
	private int preY;
	//记录权值
	private int price;
	public MyMap() {
		preX = 0;
		preY = 0;
		price = 0;
	}
	public int getPreX() {
		return preX;
	}
	public void setPreX(int preX) {
		this.preX = preX;
	}
	public int getPreY() {
		return preY;
	}
	public void setPreY(int preY) {
		this.preY = preY;
	}
	public int getPrice() {
		return price;
	}
	public void setPrice(int price) {
		this.price = price;
	}
}

test.java

import java.util.LinkedList;
import java.util.Queue;

public class test {
	static  char[][] M = {
			{' ',' ',' ',' ',' ',' ',' ',' ',' ',' '},
			{' ',' ',' ',' ','#','#','#',' ',' ',' '},
			{' ',' ',' ',' ',' ',' ','#',' ',' ',' '},
			{' ',' ',' ',' ','#','E','#',' ',' ',' '},
			{' ',' ',' ',' ','#','#','#',' ',' ',' '},
			{' ',' ',' ',' ',' ',' ',' ',' ',' ',' '},
			{' ',' ',' ',' ',' ',' ',' ',' ',' ',' '},
			{'#','#','#','#','#','#','#','#','#',' '},
			{' ',' ',' ',' ',' ',' ',' ',' ',' ',' '},
			{'S',' ',' ',' ',' ',' ',' ',' ',' ',' '}
	};
	static int[] dx = { -1,0,1,1,1,0,-1,-1 };  //x方向
	static int[] dy = { -1,-1,-1,0,1,1,1,0};//y方向
	public static Point start = null;
	public static Point end = null;
	
	public static void main(String[] args) {
		
		//获取起始点和结束点
		for(int i = 0;i < 10;i++) {
			for(int j = 0;j < 10;j++) {
				if(M[i][j] == 'S') {
					start = new Point(j,i);
				}
				if(M[i][j] == 'E') {
					end = new Point(j,i);
				}
			}
		}
		//开始遍历
		bfs();
		
		//从结束点开始打印出路径
		for(int i = 0;i < 10;i++) {
			for(int j = 0;j < 10;j++) {
				System.out.print(M[i][j]);
			}
			System.out.println();
		}
		
		
	}
	/////////////广度优先部分,主要寻路在这里//////////
	public static void bfs() {
		//队列进行记录待遍历的点
		Queue queue = new LinkedList<>();
		//将起始点加入队列
		queue.add(start);
		//设置与地图等大的MyMap
		MyMap[][] my = new MyMap[10][10];
		for(int m = 0;m < 10;m++) {
			for(int n = 0;n < 10;n++) {
				my[m][n] = new MyMap();
			}
		}
		//开始遍历
		while(queue.size() > 0) {
			//队列头进行遍历
			Point p = queue.poll();
			//8个方向
			for(int i = 0;i < 8;i++) {
				int nx = p.getX() + dx[i];
				int ny = p.getY() + dy[i];
				
				if(nx >= 0 && nx < 10 && ny >= 0 && ny < 10 && M[ny][nx] != '#') {
					//第一次访问
					if(my[ny][nx].getPrice() == 0) {
						queue.add(new Point(nx,ny));
						if((dx[i] == -1 && dy[i] == -1) || (dx[i] == -1 && dy[i] == 1) || (dx[i] == 1 && dy[i] == -1) || (dx[i] == 1 && dy[i] == 1)) {
							my[ny][nx].setPrice(my[p.getY()][p.getX()].getPrice() + 14);
						}else {
							my[ny][nx].setPrice(my[p.getY()][p.getX()].getPrice() + 10);
						}
						my[ny][nx].setPreX(p.getX());
						my[ny][nx].setPreY(p.getY());
						
					}else {
						//二次访问不用加入队列，
						if((dx[i] == -1 && dy[i] == -1) || (dx[i] == -1 && dy[i] == 1) || (dx[i] == 1 && dy[i] == -1) || (dx[i] == 1 && dy[i] == 1)) {
							if(my[p.getY()][p.getX()].getPrice() + 14 <= my[ny][nx].getPrice()) {
								my[ny][nx].setPrice(my[p.getY()][p.getX()].getPrice() + 14);
								my[ny][nx].setPreX(p.getX());
								my[ny][nx].setPreY(p.getY());
							}
						}else {
							if(my[p.getY()][p.getX()].getPrice() + 10 < my[ny][nx].getPrice()) {
								my[ny][nx].setPrice(my[p.getY()][p.getX()].getPrice() + 10);
								my[ny][nx].setPreX(p.getX());
								my[ny][nx].setPreY(p.getY());
							}
						}
					}
					
					
				}
				
			}
			
			//////////////////以下部分只是打印不重要//////////////////
			//到达目的地后
			if(p.getX() == end.getX() && p.getY() == end.getY()) {
				int x = p.getX();
				int y = p.getY();
				int tmpx = 0;
				int tmpy = 0;
				//打印
				while(x != start.getX() || y != start.getY()) {
					tmpx = my[y][x].getPreX();
					tmpy = my[y][x].getPreY();
					x = tmpx;
					y = tmpy;
					if(M[y][x] != 'S') {
						M[y][x] = '*';
					}
				}
				break;
			}
		}
	}
}

效果

类的解释：

      Point.java里面写的就是一个点的类里面就是装的x，y没啥说的。MyMap.java写的类就是记录前一个点的位置prex 和prey其实这两个参数用一个Point来记就好了。还有一个最重要的就是那个price，记录到达当前点所需要的消耗。也就是路径长度。然后就是test.java了。test当中就是bfs函数最重要了。

大体遍历的思路：

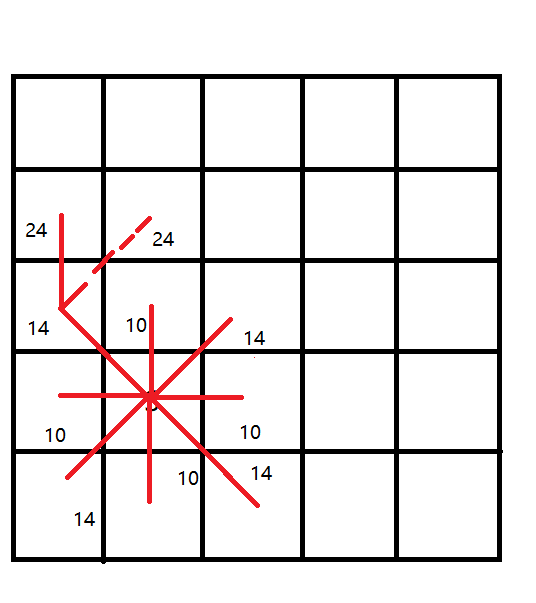
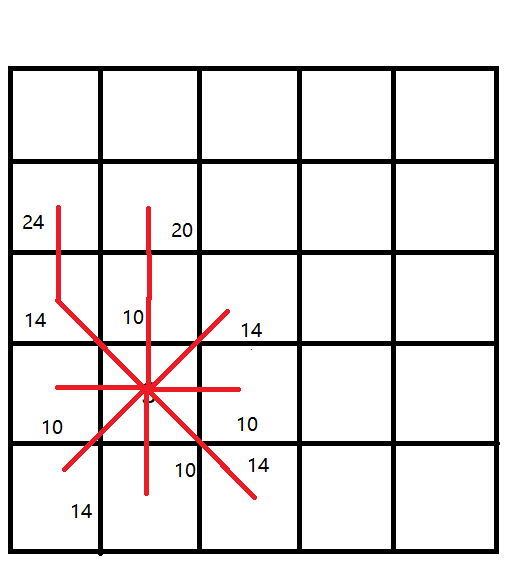
      将开始节点加入队列，然后在循环中先读出队列头，即出队列，读出的头就是当前节点，围绕该节点遍历周围的所有节点，分为：左上，上，右上，右，右下，下，左下，左共8个方向。然后将周围的节点依次加入到队列中，并且设置该节点的权值和前一节点坐标。不断循环重复以上操作，逐层遍历直到找到目的节点，或者队列为空，若队列为空都没有找到目标节点那么就是该节点不可达。

程序的超详细实现过程：

       首先为了方便起见设置一个char类型的二维数组当做地图，大小是10*10的。然后遍历找到起始点和结束点的位置坐标，Point类型的start和end。还有dx和dy两个数组。里面存的是遍历的顺序，也就是坐标的偏移量，两个数组每个都是8个元素，因为是8个方向的嘛。然后直接进重点bfs()函数，先建立一个queue队列，将开始节点加入队列，设置与地图等大的MyMap类的一个数组，并初始化。

      开始遍历，一个while循环，循环条件是queue大小要大于0，循环体中则是读出队列头，出队列，一个for循环用来遍历该点周围8个方向的点，当然要有约束条件周围的点不能超过10*10的范围同时不能为墙壁，判断墙壁用的是之前char数组的地图，而遍历记录price和前一个点的坐标的是那个MyMap数组。queue出来的点为当前点，遍历的是周围点，周围的点因为是8个方向，当扩大的时候必然会存在重复遍历的问题，不能单纯的用一个布尔来标记是否重复遍历，因为如果遍历到就进行标记的话，得到的路径不一定是最短的。因此我用的是一个price来记录到达该点的路径长度，判断是否遍历过了也很简单，如果price为0的话那么说就是第一次遍历，若不为0那就说明不是第一次遍历。两种情况分开讨论。（1）第一次遍历到该点：因为是第一次遍历到，所以要先将其加入到队列中，然后将设置消耗price，就是获取当前点（队列里出来的点）的price加上两点间路径长度，两点间路径长度：斜对角是14，上下左右相邻是10。为什么这么设，其实就是勾股定理的出来乘以10，也可以不这么设定只要相邻的距离相加大于斜对角距离就可以，满足三角形两边之和大于第三边就可以。然后设置前一点坐标为当前点。（2）第二次遍历到该点：因为不是第一次了，所以这里就不用再将其加入队列中，这里要做的就是判断应不应该与这个点连线，怎么说呢，因为他已经有price记录了，说明他已经有主子了，那么此时就要判断他指向的主子称不称职。那他的price与自己的price加上距离进行比较，如果他的price较小说明主子很称职，也就是路径较短，如果自己的price加距离要小于他自己的price说明他当前的主子不称职，就改变他的前一点的标记，改成当前点的坐标，并改变price值。如此一来可以保证到达每个点都是最小权值，按照点记录的前一点坐标进行回溯即可得到到达点的最短路径。

发现节点重复后判断消耗，发现有更好的路径则改记录坐标和消耗值

然后找到路径直接回溯，更改地图，将走过的节点改为‘*’符号，最后整体打印地图。即为最短路径。这个算法寻路效率与A*算法相比还是比较低。不过还是挺好理解的。