实验3 hopfield实现八皇后问题
传送门(所有的实验都使用python实现)
实验1 BP神经网络实验
实验2 som网实验
实验3 hopfield实现八皇后问题
实验4 模糊搜索算法预测薄冰厚度
实验5 遗传算法求解tsp问题
实验6 蚁群算法求解tsp问题
实验7 粒子群优化算法求解tsp问题
实验8 分布估计算法求解背包问题
实验9 模拟退火算法求解背包问题
实验10 禁忌搜索算法求解tsp问题
一、实验目的
理解并使用hopfile算法
二、实验内容
用hopfile实现八皇后问题。
三、实验环境
使用Python3.0 在 eclipse进行编辑
四、实验步骤
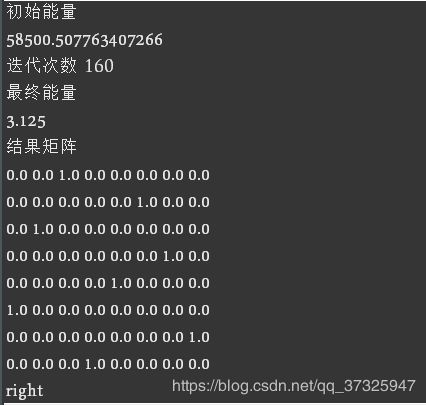
运行结果展示:
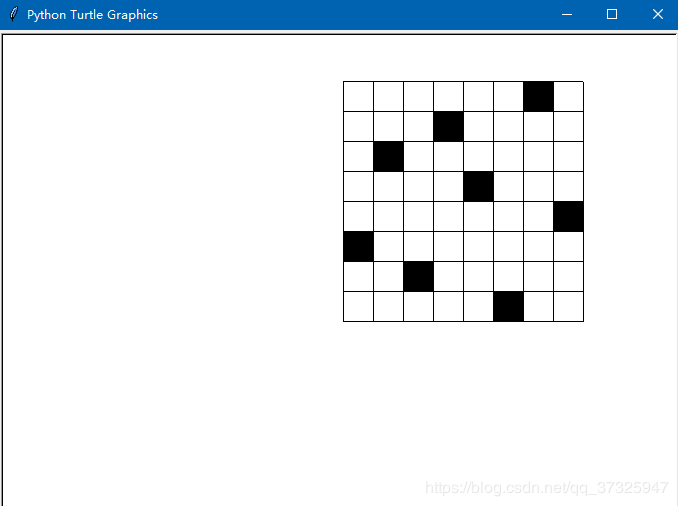
棋盘展示:
五、总结
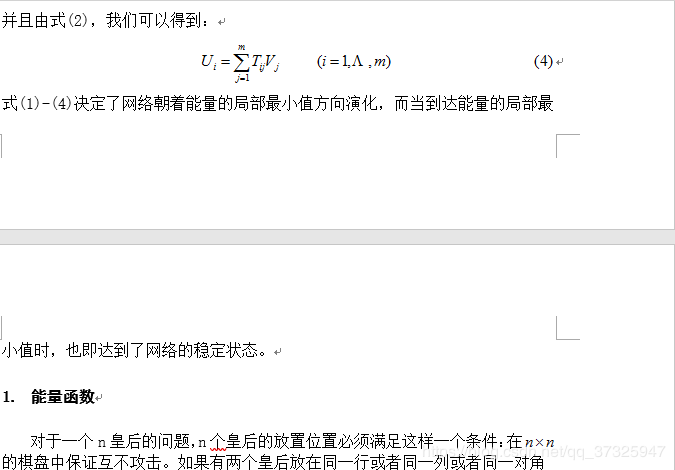
实验表明Hopfield网络具有一定的不稳定性,虽然大多数时候能够收敛到一个可行解,但有时会出现能量函数的收敛结果依然较大,主要是因为sumA、sumB1、sumB2、sumB3、sumB4某个值不为0,只要这几个值均为0,则收敛的结果必为可行解。另外实验也发现A、B、C值的设定也影响较大,如果一旦没设定好,有可能根本就不收敛,一直迭代下去。
python源码
#coding:gbk
import random
import math
import turtle
u = [[0.0]*100 for i in range(100)] #输入电压
v = [[0.0]*100 for i in range(100)] #输出电压
que = [0.0]*10; pos=0; #que数组与pos模拟队列,当连续25次的能量函数的方差为0就是稳定状态
A=100;B=100;C=100; #能量系数
n=0; g=15; n_=8.25; # n为棋盘直径,g为是sigmoid函数的增益 n_为常量
class no: #该类记录每个点的坐标
def __init__(self,x,y):
self.x=x;
self.y=y;
def draw(i ,j): #画图函数 将坐标为(i,j)空格涂黑
turtle.goto(i, j)
turtle.pendown()
turtle.begin_fill()
turtle.color("black")
turtle.forward(30)
turtle.left(90)
turtle.forward(30)
turtle.left(90)
turtle.forward(30)
turtle.left(90)
turtle.forward(30)
turtle.left(90)
turtle.end_fill()
turtle.penup()
def process(x): #算法实现函数 x为棋盘直径
global n,pos;
n=x;
init();
co = 0;
while checkEng()== 0:
co+=1;
for k in range(1,n+1):
for l in range(1,n+1):
i=random.randint(1,n);
j=random.randint(1,n);
u[i][j] = calcU(i, j); #输入电压更新
v[i][j] = calcV(i, j); #输出电压更新
if(co%5==0): #每五次记录一次能量值
que[pos]=calcEnergy(); #加入队列
#print(co,"++",que[pos])
pos+=1;
pos%=5;
print("迭代次数",co)
print("最终能量")
print(calcEnergy())
def checkEng(): #方差检查函数
sum1=0.0;
for i in range(5):
sum1+=que[i];
sum1/=5;
cnt=0.0;
for i in range(5):
cnt+=math.pow(que[i]-sum1,2);
# print("cnt=",cnt);
if(cnt/5==0):
return 1;
else:
return 0;
def init(): #能量值初始化
for i in range(1,n+1):
for j in range(1,n+1):
v[i][j]=random.random();
for i in range(5): #队列初始化
que[i]=i;
print("初始能量")
print(calcEnergy())
def calcEnergy(): #能量值计算
sumA=0.0; #sumA计算
for i in range(1,n+1):
for j in range(1,n+1):
sumRow=0.0;
for k in range(1,n+1):
if(k!=j):
sumRow+=v[i][k];
sumColumn=0.0;
for k in range(1,n+1):
if(k!=i):
sumColumn+=v[k][j];
sumA+=(sumRow + sumColumn) * v[i][j];
sumA *= A;
sumB1 = 0.0; #sumB1计算
for i in range(2,n+1):
for j in range(1,i):
sumDiagonal=0.0;
for k in range(i-j+1,n+1):
if(k!=i):
sumDiagonal += v[k][k - i + j];
sumB1 += sumDiagonal * v[i][j];
sumB1 *= B;
sumB2 = 0; #sumB2计算
for i in range(1,n+1):
for j in range(i,n+1):
sumDiagonal=0.0;
for k in range(1,n+i-j):
if(k!=i):
sumDiagonal += v[k][k - i + j];
sumB2 += sumDiagonal * v[i][j];
sumB2 *= B;
sumB3 = 0; #sumB3计算
for i in range(1,n+1):
for j in range(n-i+1,n+1):
sumDiagonal=0.0;
for k in range(i+j-n,n+1):
if(k!=i):
sumDiagonal += v[k][i + j - k];
sumB3 += sumDiagonal * v[i][j];
sumB3 *= B;
sumB4 = 0; #sumB4计算
for i in range(1,n):
for j in range(1,n-i+1):
sumDiagonal=0.0;
for k in range(1,i+j-1):
if(k!=i):
sumDiagonal += v[k][i + j - k];
sumB4 += sumDiagonal * v[i][j];
sumB4 *= B;
sumC = 0.0; #sumC计算
for i in range(1,n+1):
for j in range(1,n+1):
sumC +=v[i][j];
sumC=C*math.pow(sumC-n_,2);
#print("sumA=",sumA,"sumB1=",sumB1,"sumB2=",sumB2,"sumB3=",sumB3,"sumA=",sumA,"sumC=",sumC);
return 0.5 * (sumA + sumB1 + sumB2 + sumB3 + sumB4 + sumC);
def calcU(i,j): #输入电压计算
sumA = 0.0;
for k in range(1,n+1):
if (k != j):
sumA += v[i][k];
for k in range(1,n+1):
if (k != i):
sumA += v[k][j];
sumA *= A;
sumR = 0.0;
if (i - j > 0):
for k in range(i-j+1,n+1):
if (k != i):
sumR += v[k][k - i + j];
else:
for k in range(1,n+i-j+1):
if (k != i):
sumR += v[k][k - i + j];
sumR *= B;
sumS = 0.0;
if (i + j > n):
for k in range(i+j-n,n+1):
if (k != i):
sumS += v[k][i + j - k];
else:
for k in range(1,i+j):
if (k != i):
sumS += v[k][i + j - k];
sumS *= B;
sumC = 0.0;
for k in range(1,n+1):
for l in range(1,n+1):
sumC += v[k][l];
sumC = C * (sumC - n_);
return -(sumA + sumR + sumS + sumC);
def calcV(i,j): #输出电压计算
return 0.5 * (1 + math.tanh(g * u[i][j]));
def printResult(): #结果打印
print("结果矩阵")
p =[] #将n个皇后的坐标存在序列中
for i in range(1,n+1):
for j in range(1,n+1):
print(v[i][j],end=" "); #打印该位置状态
if(v[i][j]!=0): #如果有皇后,加入序列
p.append(no(i,j));
print("");
ok = 1;
for i in range(8):#对于加入的八个皇后的坐标进行暴力检查是否冲突
t1=p[i];
for j in range(8):
t2=p[j];
if(i==j):
continue;
if(t1.x+t1.y==t2.x+t2.y or t2.x-t1.x==t2.y-t1.y or t1.x==t2.x or t1.y==t2.y): #其中一项符合即为冲突
ok=0;
if(ok == 1): #ok==1说明此次计算结果为正确
print("right")
else:
print("wrong")
def drawResult(): #将8*8的棋盘画出来
# turtle.Turtle().screen.delay(0)
turtle.speed(8) #画笔速度
# turtle.pensize(1)
turtle.penup()
turtle.color("black") #黑色画笔
for i in range(0,270,30):
turtle.goto(0, i)
turtle.pendown()
turtle.forward(240)
turtle.penup()
turtle.left(90)
for i in range(0,270,30):
turtle.goto(i, 0)
turtle.pendown()
turtle.forward(240)
turtle.penup()
turtle.right(90)
for i in range(1,n+1): #将8个皇后的位置涂黑
for j in range(1,n+1):
if(v[i][j] != 0):
draw((i-1)*30,(j-1)*30)
turtle.hideturtle() #隐藏画笔
turtle.done()
#x = input();
x=8
process(int(x)); #执行算法
printResult(); #打印结果
drawResult(); #描绘棋盘