深度学习之卷积神经网络详解及代码演示
一、卷积神经网络介绍
卷积神经网络广泛应用于计算机视觉领域。就处理图像数据来说,由于一幅图像有许多像素点和通道数,人工神经网络需要很多的权重值w,这样会大大损耗计算资源,也很容易造成过拟合现象。因此,产生了卷积神经网络,仅需很少的神经元就可以对图像进行很好地训练。
卷积神经网络主要有以下层次:
1、数据输入层/ input layer
2、卷积计算层/ conv layer
3、ReLU激励层/ ReLU layer
4、池化层/ Pooling layer
5、全连接层/ FC layer
6、Batch Normalization层(一般没有)
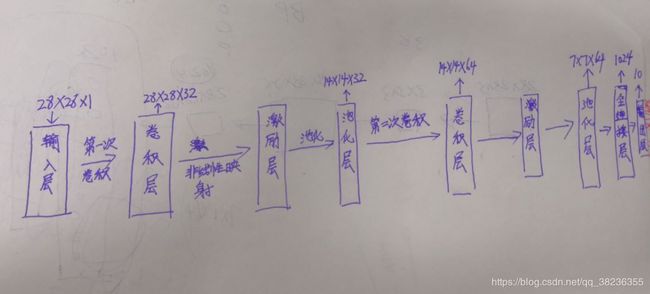
各层之间连接顺序如下图所示:
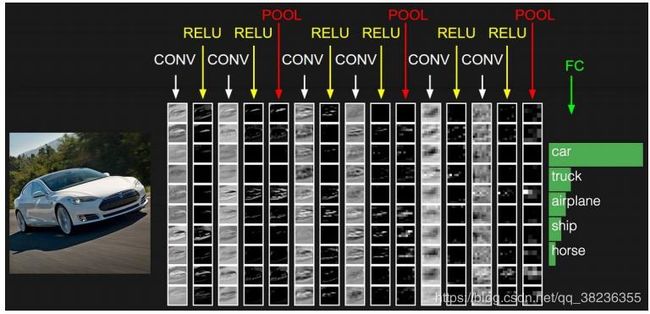
该图演示了卷积神经网络识别汽车图片的过程,经过几层卷积和池化后,输出的为预测的概率大小。
下面详细讲解下每一层次的结构内容:
1、数据输入层:
该层要做的处理主要是对原始图像数据进行预处理,其中包括:
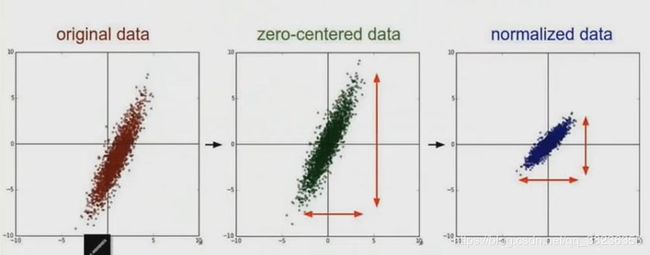
• 去均值:把输入数据各个维度都中心化为0,如下图所示,其目的就是把样本的中心拉回到坐标系原点上。(每个数据都减去该维度数据的平均值)
• 归一化:幅度归一化到同样的范围,如下所示,即减少各维度数据取值范围的差异而带来的干扰,比如,我们有两个维度的特征A和B,A范围是0到10,而B范围是0到10000,如果直接使用这两个特征是有问题的,好的做法就是归一化,即A和B的数据都变为0到1的范围。
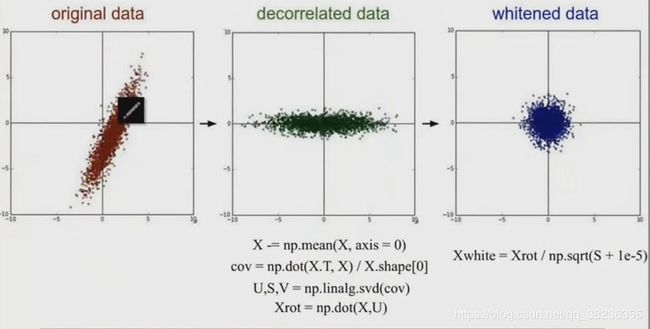
• PCA/白化:用PCA降维;白化是对数据各个特征轴上的幅度归一化
去均值与归一化效果图:
PCA和白化效果图:
2、卷积计算层
这一层就是卷积神经网络最重要的一个层次,也是“卷积神经网络”的名字来源。
在这个卷积层,有两个关键操作:
• 局部关联。每个神经元看做一个滤波器(filter)
• 窗口(receptive field)滑动, filter对局部数据计算
先介绍卷积层遇到的几个名词:
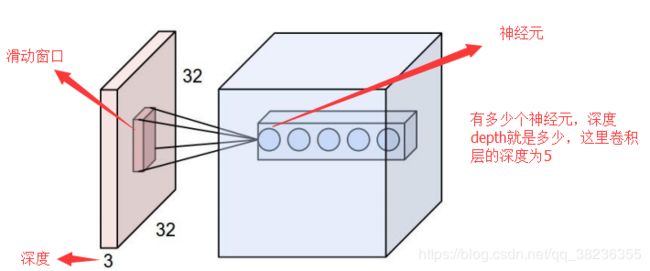
• 深度/depth(解释见下图)
• 步长/stride (窗口一次滑动的长度)
• 填充值/zero-padding
卷积层深度/depth与神经元的个数相等,如下图中有五个神经元ABCDE,卷积层的深度就是5,即有5组不同的窗口分别对图像进行卷积计算,得到的特征图像的通道数也是5。
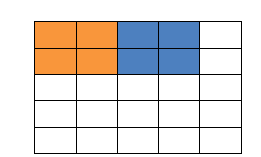
填充值是什么呢?以下图为例子,比如有这么一个55的图片(一个格子一个像素),我们滑动窗口取22,步长取2,那么我们发现还剩下1个像素没法滑完,那怎么办呢?
那我们在原先的矩阵加了一层填充值,使得变成6*6的矩阵,那么窗口就可以刚好把所有像素遍历完。这就是填充值的作用。
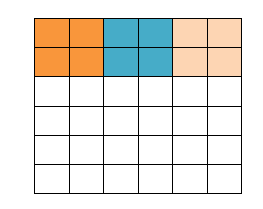
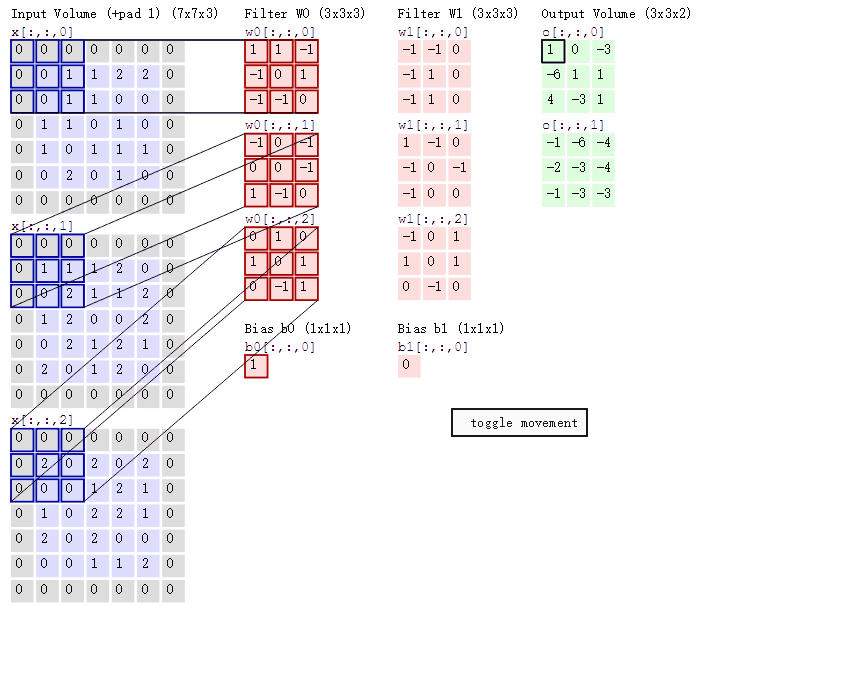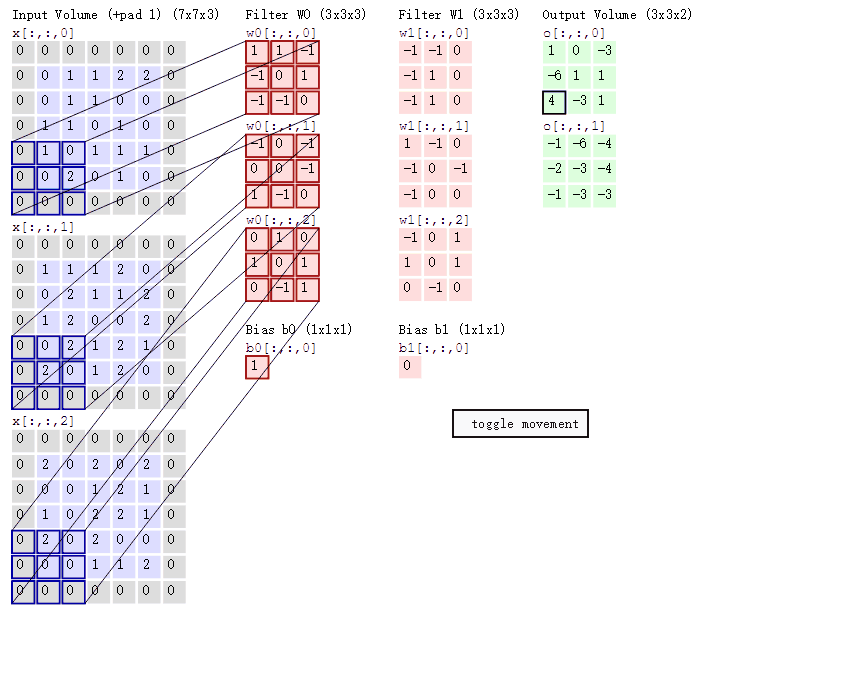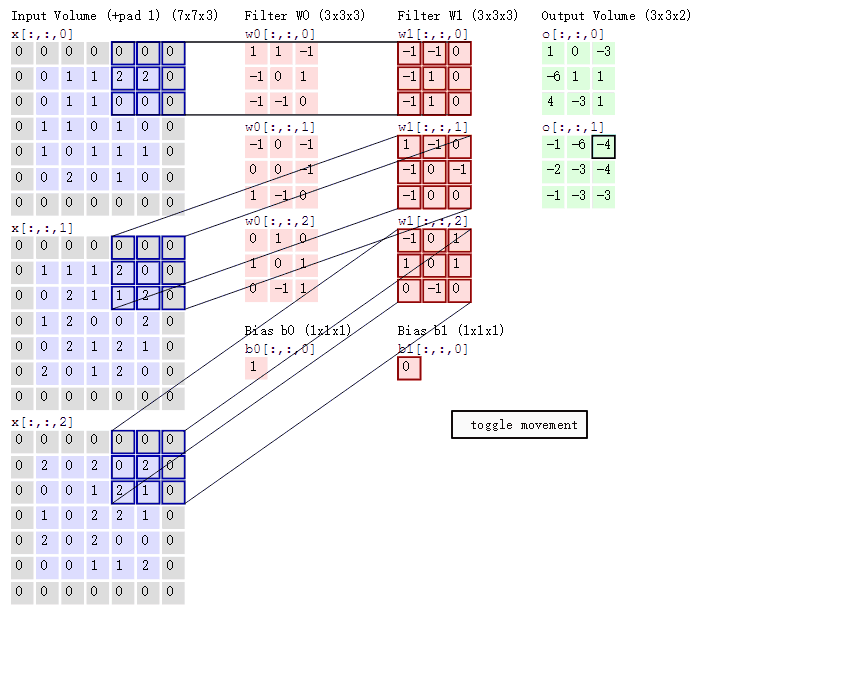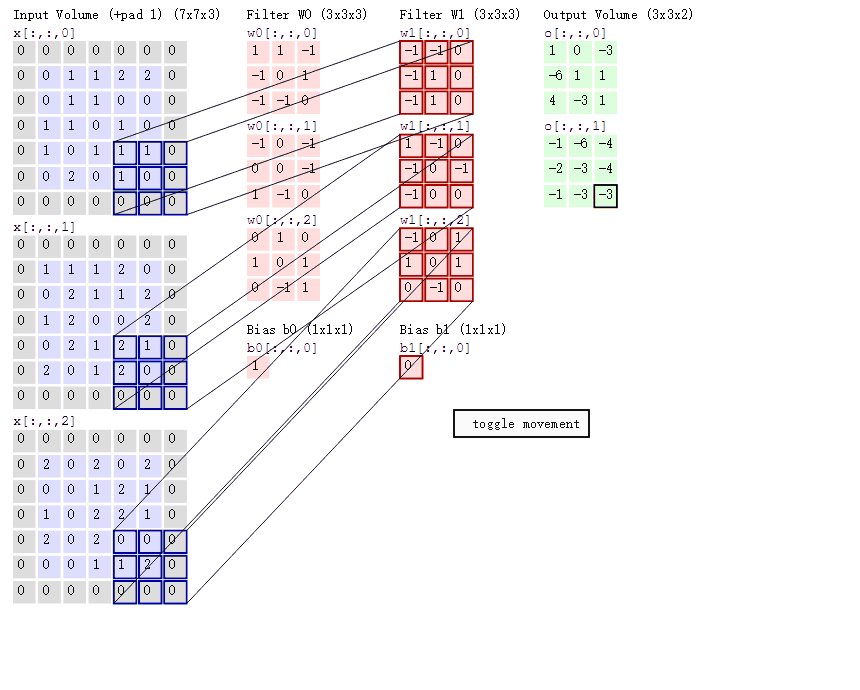
卷积的计算(注意,下面蓝色矩阵周围有一圈灰色的框,那些就是上面所说到的填充值)

这里的蓝色矩阵就是输入的图像(因为彩色图像有BGR三个通道,所以对应有三个图像矩阵),粉色矩阵就是卷积层的神经元,这里表示了有两个神经元(w0,w1)即深度为2。绿色矩阵就是经过卷积运算后的输出矩阵,这里的步长设置为2。
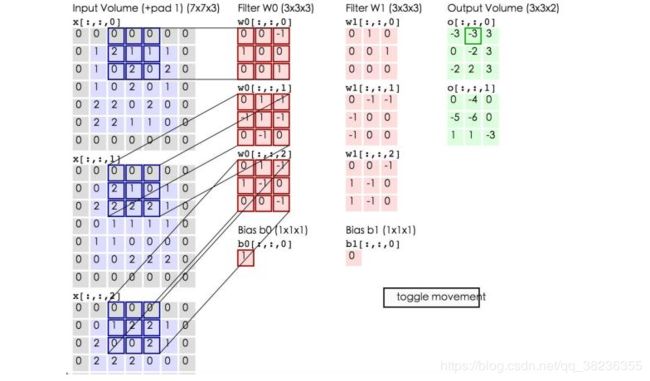
三个蓝色的矩阵(输入图像)对三个粉色的矩阵(filter)分别进行矩阵内积计算并将三个内积运算的结果与偏置值b相加(比如上面图的计算:2+(-2+1-2)+(1-2-2) + 1= 2 - 3 - 3 + 1 = -3),计算后的值就是绿框矩阵的一个元素。

下面的动态图形象地展示了卷积层的计算过程:
参数共享机制
• 在卷积层中每个神经元连接数据窗的权重是固定的,每个神经元只关注一个特性。神经元就是图像处理中的滤波器,比如边缘检测专用的Sobel滤波器,即卷积层的每个滤波器都会有自己所关注一个图像特征,比如垂直边缘,水平边缘,颜色,纹理等等,这些所有神经元加起来就好比就是整张图像的特征提取器集合。
• 需要估算的权重个数减少: AlexNet 1亿 => 3.5w
• 一组固定的权重和不同窗口内数据做内积: 卷积
3、激励层
把卷积层输出结果做非线性映射。
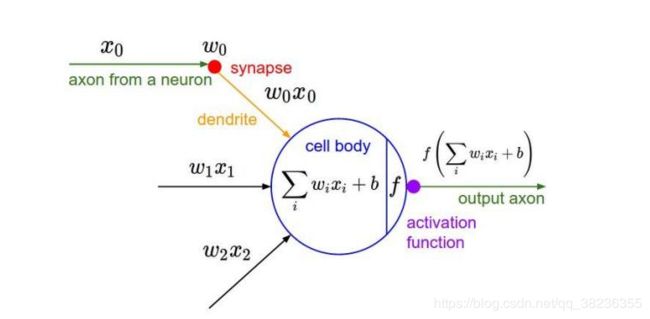
这里f代表进行的非线性映射操作。常见的非线性映射有以下几种:

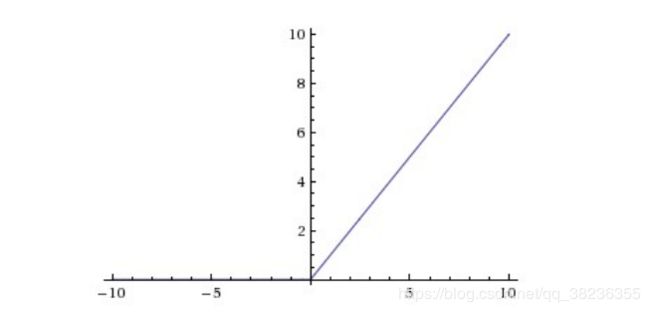
CNN采用的激励函数一般为ReLU(The Rectified Linear Unit/修正线性单元),它的特点是收敛快,求梯度简单,但较脆弱,图像如下。
激励层的实践经验:
①不要用sigmoid!不要用sigmoid!不要用sigmoid!避免产生梯度消失
② 首先试RELU,因为快,但要小心点
③ 如果2失效,请用Leaky ReLU或者Maxout
④ 某些情况下tanh倒是有不错的结果,但是很少
4.池化层
池化层夹在连续的卷积层中间, 用于压缩数据和参数的量,减小过拟合。简而言之,如果输入是图像的话,那么池化层的最主要作用就是压缩图像。
这里再展开叙述池化层的具体作用。
-
特征不变性,也就是我们在图像处理中经常提到的特征的尺度不变性,池化操作就是图像的resize,平时一张狗的图像被缩小了一倍我们还能认出这是一张狗的照片,这说明这张图像中仍保留着狗最重要的特征,我们一看就能判断图像中画的是一只狗,图像压缩时去掉的信息只是一些无关紧要的信息,而留下的信息则是具有尺度不变性的特征,是最能表达图像的特征。
-
特征降维,我们知道一幅图像含有的信息是很大的,特征也很多,但是有些信息对于我们做图像任务时没有太多用途或者有重复,我们可以把这类冗余信息去除,把最重要的特征抽取出来,这也是池化操作的一大作用。
-
在一定程度上防止过拟合,更方便优化。
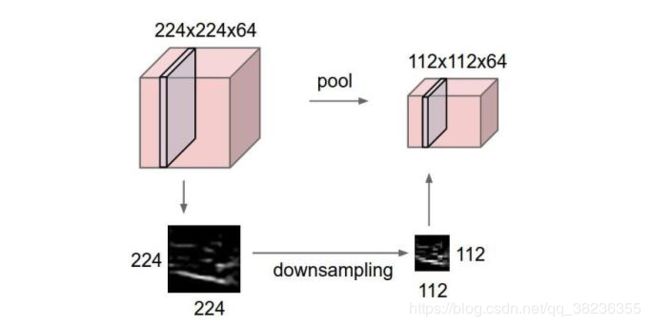
池化层用的方法有Max pooling 和 average pooling,而实际用的较多的是Max pooling。
这里就说一下Max pooling,其实思想非常简单。
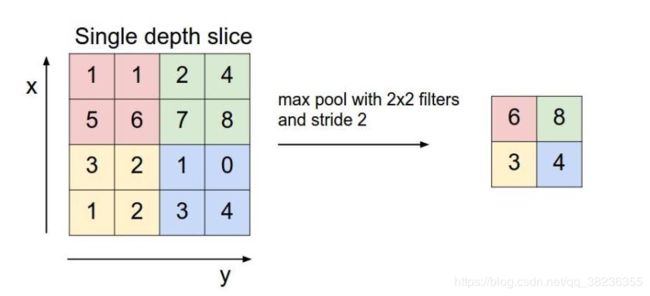
对于每个22的窗口选出最大的数作为输出矩阵的相应元素的值,比如输入矩阵第一个22窗口中最大的数是6,那么输出矩阵的第一个元素就是6,如此类推。
5.全连接层
两层之间所有神经元都有权重连接,通常全连接层在卷积神经网络尾部(在最后一层卷积池化和输出层之间)。也就是跟传统的神经网络神经元的连接方式是一样的:

一般CNN结构依次为
1. INPUT
2. [[CONV -> RELU]*N -> POOL?]*M
3. [FC -> RELU]*K
4. FC
二、卷积神经网络训练算法
同一般机器学习算法,先定义Loss function,衡量和实际结果之间的差距,然后找到最小化损失函数的w和b,CNN中用的算法是SGD。SGD需要计算w和b的偏导,BP算法就是计算偏导用的,BP算法的核心是求导链式法则。BP算法利用链式求导法则,逐级相乘直到求解出dw和db,然后利用SGD/随机梯度下降,迭代和更新w和b。详细内容参考:https://blog.csdn.net/qq_38236355/article/details/89477700
三、卷积神经网络优缺点
优点:
1、共享卷积核,对高维数据处理无压力;
2、无需手动选取特征,训练好权重,即得特征;
3、深层次的网络抽取图像信息丰富,表达效果好。
缺点:
1、需要调参,需要大样本量,训练最好要用GPU;
2、物理含义不明确。
四、正则化与Dropout
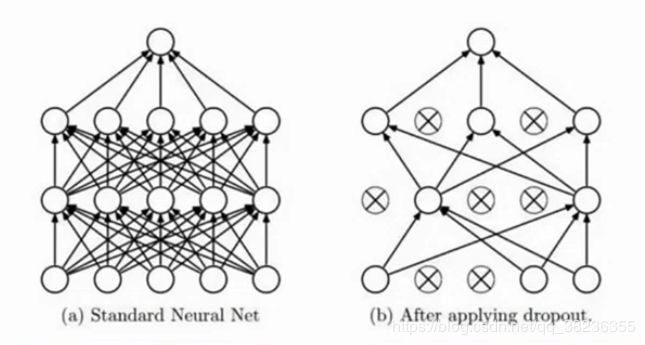
神经网络学习能力强可能会过拟合。Dropout(随机失活)正则化:别一次开启所有学习单元,每次随机关闭一些神经元。如下图所示:
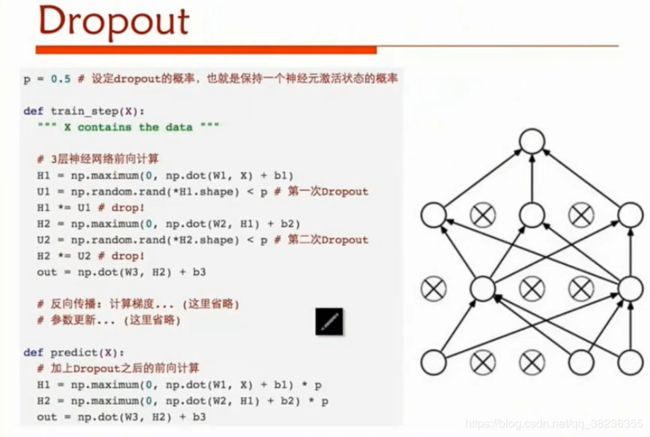
实际代码演示如下:

防止过拟合的第一种理解方式:别让你的神经网络记住那么多东西(虽然CNN记忆力好),例如识别猫的图片的CNN神经网络,就是一只猫而已,要有一些泛化能力。

防止过拟合的第二种理解方式:每次都关掉一部分感知器,得到一个新模型,最后做融合,不至于听一家所言。
我们这里用tensorflow官方中文教程里的构建卷积神经网络进行MNIST预测的例程进行讲解:
from tensorflow.examples.tutorials.mnist import input_data # 引入MNIST数据集
import tensorflow as tf
mnist = input_data.read_data_sets('MNIST_data', one_hot=True) # 将数据存到MNIST_data文件中,并读取到mnist中
sess = tf.InteractiveSession() # 启动图
x = tf.placeholder("float", shape=[None, 784]) # n张28*28的图像,None为占位符
y_ = tf.placeholder("float", shape=[None, 10]) # 标签对应0-9 十个数
# 定义两个函数用于初始化
def weight_variable(shape): # 权重,加入少量的噪声0.1来打破对称性以及避免0梯度
initial = tf.truncated_normal(shape, stddev=0.1)
return tf.Variable(initial)
def bias_variable(shape): #偏置项,用一个较小的正数来初始化偏置项,以避免神经元节点输出恒为0的问题(dead neurons)
initial = tf.constant(0.1, shape=shape)
return tf.Variable(initial)
# 卷积和池化
def conv2d(x, w):
return tf.nn.conv2d(x, w, strides=[1, 1, 1, 1], padding='SAME') # strides中间两个1表示上下左右的步长都是1
def max_pool_2x2(x):
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME') # 池化窗口大小为2*2,步长也是2.
# 第一层卷积
w_conv1 = weight_variable([5, 5, 1, 32]) # 5x5窗口大小,第三个参数为通道数,第四个参数为深度32,即32个神经元,得到32个特征图。
b_conve1 = bias_variable([32]) # 偏执项
x_image = tf.reshape(x, [-1, 28, 28, 1]) # [mini-batch size, height, width, channels]
h_conv1 = tf.nn.relu(conv2d(x_image, w_conv1) + b_conve1) # 卷积计算+relu激励层
h_pool1 = max_pool_2x2(h_conv1) # 池化层,得到32个图,池化结果每幅图大小14*14
# 第二层卷积
w_conv2 = weight_variable([5, 5, 32, 64]) # 5x5大小,32通道(对应第一层池化得到的32个图),64个神经元,得64个特征图
b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1, w_conv2) + b_conv2) # 对第一层池化后结果做卷积计算+relu激励
h_pool2 = max_pool_2x2(h_conv2) # 池化层,池化结果每幅图大小7*7
# 密集连接层
w_fc1 = weight_variable([7 * 7 * 64, 1024]) # 第一个参数为图像大小7*7,通道数64。全连接层要产生1024个神经元
b_fc1 = bias_variable([1024])
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, w_fc1)+b_fc1) # 矩阵乘法+relu激励
# Dropout,为了减少过拟合,我们在输出层之前加入dropout。
keep_prob = tf.placeholder("float")
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)
# 输出层 softmax层
w_fc2 = weight_variable([1024, 10]) # 输出层有10个概率,对应0-9十个数
b_fc2 = bias_variable([10])
y_conv=tf.nn.softmax(tf.matmul(h_fc1_drop, w_fc2)+b_fc2)
# 训练和评估模型, 用更加复杂的ADAM优化器来做梯度最速下降
cross_entropy = -tf.reduce_sum(y_*tf.log(y_conv))
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
sess.run(tf.initialize_all_variables())
for i in range(20000):
batch = mnist.train.next_batch(50)
if i%100 == 0:
train_accuracy = accuracy.eval(feed_dict={x: batch[0], y_: batch[1], keep_prob: 1.0})
print("step %d, training accuracy %g"%(i, train_accuracy))
train_step.run(feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})
print("test accuracy %g"%accuracy.eval(feed_dict={x: mnist.test.images, y_: mnist.test.labels, keep_prob: 1.0}))
整个代码的卷积神经网络结构如下图所示: