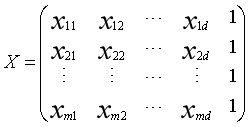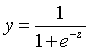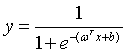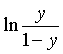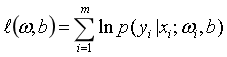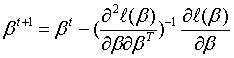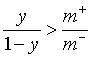机器学习笔记（三）
一、线性模型的基本形式
线性模型一般形式：f（x）=w1*x1+w2*x2+……+wm*xm+b；x=（x1，......，xm）是属性描述的示例。
向量形式：f（x）=wT*x+b；w=（w1，......，wm）。
二、线性回归
单一属性的线性回归目标：f（x）=wi+b；使得f（xi）≈ yi；
参数/模型估计：最小二乘法（least square method）
（w*，b*）= argminΣ（f（xi）-yi）^2（i=1，......，m）或者argminΣ（yi-w*xi-b）^2；
最小化均方误差E(w,b)=Σ（yi-w*xi-b）^2。
给定数据集D={（x1，y1），.....，（xm，ym）}，其中xi=（xi1；xi2；.....；xid）。
有f（xi）=wTxi+b使得 f（xi）= yi 。
把
和
b
吸收入向量
形式
=(
;b)
，数据集表示为
多元线性回归- 最小二乘法：
则有线性回归模型
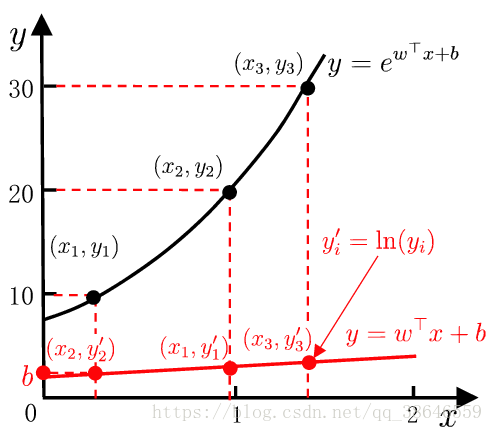
对数线性回归 
如下图
广义线性模型 
三、二分类任务
预测值与输出标记 
y属于{0,1}。
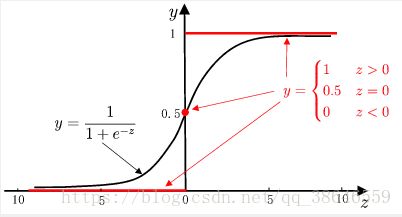
寻找函数将分类标记与线性回归模型输出联系起来，最理想的函数——单位阶跃函数
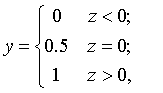预测值大于零就判为正例，小于零就判为反例，预测值为临界值零则
可任意判别。但是单位阶跃函数存在不连续的缺点，所以替代函数--对数几率函数应运而生，
，下图是对数几率函数与单位阶跃函数的比较：
对数几率函数可以变为
，样本作为正例的相对可能性的对数
。
对数几率回归优点
1. 无需事先假设数据分布
2.可得到“类别”的近似概率预测
3. 可直接应用现有数值优化算法求取最优解
极大似然法（maximum likelihood）
给定数据集
，有最大化对数似然函数
，求解得
牛顿法第t+1轮迭代解的更新公式
。
线性判别分析（Linear Discriminant Analysis）LDA的思想：
1.欲使同类样例的投影点尽可能接近，可以让同类样例投影点的协方差尽可能小。
2.欲使异类样例的投影点尽可能远离，可以让类中心之间的距离尽可能大。
多分类LDA将样本投影到N-1维空间，N-1通常远小于数据原有的属性数，因此LDA也被视为一种监督降维技术。
多分类学习
1.二分类学习方法推广到多类。
2.利用二分类学习器解决多分类问题
3.对问题进行拆分，为拆出的每个二分类任务训练一个分类器
4.对于每个分类器的预测结果进行集成以获得最终的多分类结果
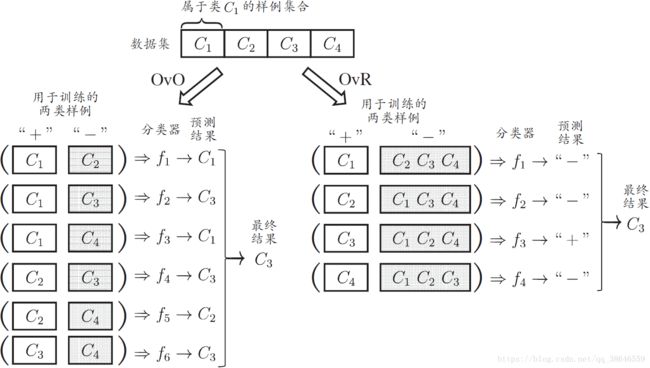
拆分策略
1.一对一（One vs. One, OvO）2.一对其余（One vs. Rest, OvR）3.多对多（Many vs. Many, MvM）。
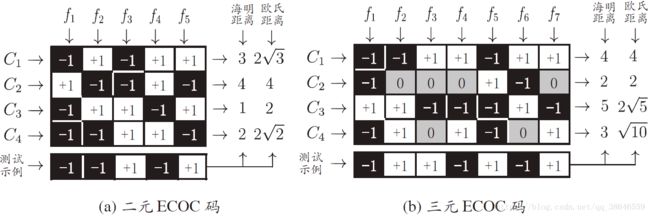
纠错输出码（Error Correcting Output Code, ECOC）
ECOC编码对分类器错误有一定容忍和修正能力，编码越长、纠错能力越强
对同等长度的编码，理论上来说，任意两个类别之间的编码距离越远，则纠错能力越强
类别不平衡（class imbalance）
.不同类别训练样例数相差很大情况（正类为小类）
正负类比例。
各任务下（回归、分类）各个模型优化的目标
1.最小二乘法：最小化均方误差
2.对数几率回归：最大化样本分布似然
3.线性判别分析：投影空间内最小（大）化类内（间）散度
参数的优化方法
1.最小二乘法：线性代数
2.对数几率回归：凸优化梯度下降、牛顿法
3.线性判别分析：矩阵论、广义瑞利商