如何理解正规方程
在《如何理解线性回归》中,我们提到了使用梯度下降来求解最小二乘问题,但在线性回归中,还有一种不需要迭代的方法来求解最小二乘问题,这就是正规方程。这是基于矩阵求导来及计算的
还是上次的数据
x = [[1, 1, 1, 1, 1], [1, 2, 3, 4, 5]]
y = [4.8, 7.2, 8.8, 11.2, 12.8]
plt.scatter(x[1], y)
plt.xlim(0,6)
plt.ylim(0,14)
plt.show()
和线性回归前半部分的理解一样,我们的目标是最小化 J J J,只是这里使用的 J J J是 J = 1 2 ∑ ( y − y h ) 2 J=\frac{1}{2}\sum(y-y_h)^2 J=21∑(y−yh)2(我们用 y y y表示真实值, y h y_h yh表示预测值),标准的写法是这样的,之前我们在用梯度下降时 J J J没有 1 / 2 1/2 1/2也没有关系。那么现在我们就要用矩阵的形式来表示 J J J,并取它的导数,当导数等于零时,也就可以得到最终的正规方程,下面是 J J J的矩阵表示
J = 1 2 ∑ ( y − y h ) 2 = 1 2 t r [ ( X θ − Y ) T ( X θ − Y ) ] \begin{aligned} J & = \frac{1}{2}∑(y - y_h)^2 \\ & = \frac{1}{2}tr[(Xθ - Y)^T (Xθ - Y)] \end{aligned} J=21∑(y−yh)2=21tr[(Xθ−Y)T(Xθ−Y)]
t r tr tr是什么, t r tr tr表示矩阵的迹,也就是矩阵主对角线元素的和,表示为 t r A = ∑ a i i trA=∑a_{ii} trA=∑aii,其中有些重要的定理
1. t r ( A B ) = t r ( B A ) 2. t r ( A + B ) = t r ( A ) + t r ( B ) 3. d ( t r ( A B ) ) / d ( A ) = B T 4. d ( t r ( A T B ) ) / d ( A ) = B 5. t r ( A ) = t r ( A T ) 6. t r ( a ) = a ( a ∈ R ) 7. d ( t r ( A B A T C ) ) / d ( A ) = C A B + C T A B T \begin{aligned} &{1.}tr(AB) = tr(BA)\\ &{2.}tr(A+B) = tr(A) + tr(B)\\ &{3.}d(tr(AB))/d(A) = B^T\\ &{4.}d(tr(A^TB))/d(A) = B\\ &{5.}tr(A) = tr(A^T)\\ &{6.}tr(a) = a(a ∈ R)\\ &{7.}d(tr(ABA^TC))/d(A) = CAB+C^TAB^T\\ \end{aligned} 1.tr(AB)=tr(BA)2.tr(A+B)=tr(A)+tr(B)3.d(tr(AB))/d(A)=BT4.d(tr(ATB))/d(A)=B5.tr(A)=tr(AT)6.tr(a)=a(a∈R)7.d(tr(ABATC))/d(A)=CAB+CTABT
就这个问题,我们可以有如下的表示
(1) x i = ( 1 x ) 这 里 的 x 就 是 上 面 的 [ 1 , 2 , 3 , 4 , 5 ] x_i= \left( \begin{matrix} 1\\ x \end{matrix} \right)\tag{1}这里的x就是上面的[1, 2, 3, 4, 5] xi=(1x)这里的x就是上面的[1,2,3,4,5](1) (2) θ = ( b a ) 这 是 y = a x + b 的 参 数 θ= \left( \begin{matrix} b\\ a \end{matrix} \right)\tag{2}这是y=ax+b的参数 θ=(ba)这是y=ax+b的参数(2) (3) X = ( x 0 T x 1 T x 2 T x 3 T x 4 T ) X= \left( \begin{matrix} x_0^T\\ x_1^T\\ x_2^T\\ x_3^T\\ x_4^T \end{matrix} \right)\tag{3} X=⎝⎜⎜⎜⎜⎛x0Tx1Tx2Tx3Tx4T⎠⎟⎟⎟⎟⎞(3) (4) Y = ( y 0 y 1 y 2 y 3 y 4 ) 这 里 的 y i 就 是 上 面 的 [ 4.8 , 7.2 , 8.8 , 11.2 , 12.8 ] Y= \left( \begin{matrix} y_0\\ y_1\\ y_2\\ y_3\\ y_4\\ \end{matrix} \right)\tag{4}这里的y_i就是上面的[4.8, 7.2, 8.8, 11.2, 12.8] Y=⎝⎜⎜⎜⎜⎛y0y1y2y3y4⎠⎟⎟⎟⎟⎞这里的yi就是上面的[4.8,7.2,8.8,11.2,12.8](4)
上面的 x x x是一个 2 × 1 2\times1 2×1的向量,这样 x T θ x^Tθ xTθ就是一个 1 × 2 1\times2 1×2的向量乘一个 2 × 1 2\times1 2×1,就得到一个答案,就是 a x + b ax+b ax+b,这个很眼熟吧。所以 X T θ − Y X^Tθ-Y XTθ−Y就包含了所有的 y − y h = a x + b − y h y-y_h=ax+b-y_h y−yh=ax+b−yh,转置相乘再去迹就可以得到所有式子的平方和。这个式子比较好理解
麻烦的就是下面 d ( J ) / d ( θ ) d(J)/d(θ) d(J)/d(θ)。首先暴力拆开 ( X θ − Y ) T ( X θ − Y ) (Xθ-Y)^T(Xθ-Y) (Xθ−Y)T(Xθ−Y)
( X θ − Y ) T ( X θ − Y ) = ( θ T X T − Y T ) ( X θ − Y ) = θ T X T X θ − θ T X T Y − Y T X θ + Y T Y \begin{aligned} (Xθ - Y)^T (Xθ - Y) & = (θ^TX^T - Y^T)(Xθ - Y)\\ &= θ^TX^TXθ - θ^TX^TY - Y^TXθ + Y^TY \end{aligned} (Xθ−Y)T(Xθ−Y)=(θTXT−YT)(Xθ−Y)=θTXTXθ−θTXTY−YTXθ+YTY
所以这时要解 d ( J ) / d ( θ ) d(J)/d(θ) d(J)/d(θ),我们算一下维度看, θ T X T X θ θ^TX^TXθ θTXTXθ是 ( 1 × 2 × 2 × 5 × 5 × 2 × 2 × 1 ) = ( 1 × 1 ) (1\times2 \times 2\times5 \times 5\times2 \times 2\times1)=(1\times1) (1×2×2×5×5×2×2×1)=(1×1), θ T X T Y θ^TX^TY θTXTY是 ( 1 × 2 × 2 × 5 × 5 × 1 ) = ( 1 × 1 ) (1\times2 \times 2\times5 \times 5\times1)=(1\times1) (1×2×2×5×5×1)=(1×1),还有 Y T X θ Y^TXθ YTXθ是 ( 1 × 5 × 5 × 2 × 2 × 1 ) = ( 1 × 1 ) (1\times5 \times 5\times2 \times 2\times1)=(1\times1) (1×5×5×2×2×1)=(1×1), Y T Y Y^TY YTY是 ( 1 × 5 × 5 × 1 ) = ( 1 × 1 ) (1\times5 \times 5\times1)=(1\times1) (1×5×5×1)=(1×1),都是些 1 × 1 1\times1 1×1的阵。苦逼没学过矩阵的求导,只有马上去学了,至少可以看出最后的 Y T Y Y^TY YTY与 θ θ θ半毛钱关系都没有,所以就可以忽略了,得到下面的式子
d ( J ) / d ( θ ) = 1 2 d ( t r ( θ T X T X θ − θ T X T Y − Y T X θ + Y T Y ) ) / d ( θ ) = 1 2 d ( t r ( θ T X T X θ − θ T X T Y − Y T X θ ) ) / d ( θ ) \begin{aligned} d(J)/d(θ) &= \frac{1}{2}d(tr(θ^TX^TXθ - θ^TX^TY - Y^TXθ + Y^TY)) / d(θ)\\ &=\frac{1}{2}d(tr(θ^TX^TXθ - θ^TX^TY - Y^TXθ)) / d(θ) \end{aligned} d(J)/d(θ)=21d(tr(θTXTXθ−θTXTY−YTXθ+YTY))/d(θ)=21d(tr(θTXTXθ−θTXTY−YTXθ))/d(θ)
然后可以发现 θ T X T Y θ^TX^TY θTXTY是 Y T X θ Y^TXθ YTXθ的转置,也就是 ( Y T X θ ) T = θ T X T Y (Y^TXθ)^T=θ^TX^TY (YTXθ)T=θTXTY。由迹的一些定理(上面的2和5),我们可以这样处理一下
d ( J ) / d ( θ ) = 1 2 d ( t r ( θ T X T X θ − θ T X T Y − Y T X θ + Y T Y ) ) / d ( θ ) = 1 2 d ( t r ( θ T X T X θ − θ T X T Y − Y T X θ ) ) / d ( θ ) = 1 2 ( d ( t r ( θ T X T X θ ) / d ( θ ) − d ( t r ( θ T X T Y ) / d ( θ ) − d ( t r ( Y T X θ ) / d ( θ ) ) = 1 2 ( d ( t r ( θ T X T X θ ) / d ( θ ) − 2 d ( t r ( θ T X T Y ) / d ( θ ) ) \begin{aligned} d(J)/d(θ) &= \frac{1}{2}d(tr(θ^TX^TXθ - θ^TX^TY - Y^TXθ + Y^TY)) / d(θ)\\ &=\frac{1}{2}d(tr(θ^TX^TXθ - θ^TX^TY - Y^TXθ)) / d(θ)\\ &=\frac{1}{2}(d(tr(θ^TX^TXθ) / d(θ) - d(tr(θ^TX^TY) / d(θ) - d(tr(Y^TXθ) / d(θ))\\ &=\frac{1}{2}(d(tr(θ^TX^TXθ) / d(θ) - 2d(tr(θ^TX^TY) / d(θ)) \end{aligned} d(J)/d(θ)=21d(tr(θTXTXθ−θTXTY−YTXθ+YTY))/d(θ)=21d(tr(θTXTXθ−θTXTY−YTXθ))/d(θ)=21(d(tr(θTXTXθ)/d(θ)−d(tr(θTXTY)/d(θ)−d(tr(YTXθ)/d(θ))=21(d(tr(θTXTXθ)/d(θ)−2d(tr(θTXTY)/d(θ))
然后现在需要求导了,这里有一些有用的求导的定理
1. d ( a ) / d ( x ) = 0 2. d ( x ) / d ( x ) = I ( I 是 单 位 矩 阵 ) 3. d ( A x ) / d ( x ) = A T 4. d ( x T A ) / d ( x ) = A 5. d ( A T B A ) / d ( A ) = ( B + B T ) A \begin{aligned} &{1.}d(a)/d(x) = 0\\ &{2.}d(x)/d(x) = I (I是单位矩阵)\\ &{3.}d(Ax)/d(x) = A^T\\ &{4.} d(x^TA)/d(x) = A\\ &{5.}d(A^TBA)/d(A) = (B+B^T)A\\ \end{aligned} 1.d(a)/d(x)=02.d(x)/d(x)=I(I是单位矩阵)3.d(Ax)/d(x)=AT4.d(xTA)/d(x)=A5.d(ATBA)/d(A)=(B+BT)A
现在就可以继续向下做了,由求导的5和迹的4可以得到如下的结果
d ( J ) / d ( θ ) = 1 2 d ( t r ( θ T X T X θ − θ T X T Y − Y T X θ + Y T Y ) ) / d ( θ ) = 1 2 d ( t r ( θ T X T X θ − θ T X T Y − Y T X θ ) ) / d ( θ ) = 1 2 ( d ( t r ( θ T X T X θ ) / d ( θ ) − d ( t r ( θ T X T Y ) / d ( θ ) − d ( t r ( Y T X θ ) / d ( θ ) ) = 1 2 ( d ( t r ( θ T X T X θ ) / d ( θ ) − 2 d ( t r ( θ T X T Y ) / d ( θ ) ) = 1 2 ( 2 X T X θ − 2 X T Y ) = X T X θ − X T Y \begin{aligned} d(J)/d(θ) &= \frac{1}{2}d(tr(θ^TX^TXθ - θ^TX^TY - Y^TXθ + Y^TY)) / d(θ)\\ &=\frac{1}{2}d(tr(θ^TX^TXθ - θ^TX^TY - Y^TXθ)) / d(θ)\\ &=\frac{1}{2}(d(tr(θ^TX^TXθ) / d(θ) - d(tr(θ^TX^TY) / d(θ) - d(tr(Y^TXθ) / d(θ))\\ &=\frac{1}{2}(d(tr(θ^TX^TXθ) / d(θ) - 2d(tr(θ^TX^TY) / d(θ))\\ &=\frac{1}{2}(2X^TXθ - 2X^TY)\\ &=X^TXθ - X^TY \end{aligned} d(J)/d(θ)=21d(tr(θTXTXθ−θTXTY−YTXθ+YTY))/d(θ)=21d(tr(θTXTXθ−θTXTY−YTXθ))/d(θ)=21(d(tr(θTXTXθ)/d(θ)−d(tr(θTXTY)/d(θ)−d(tr(YTXθ)/d(θ))=21(d(tr(θTXTXθ)/d(θ)−2d(tr(θTXTY)/d(θ))=21(2XTXθ−2XTY)=XTXθ−XTY
这是让 d ( J ) / d ( θ ) = 0 d(J)/d(θ)=0 d(J)/d(θ)=0,就是导数等于零,我们知道在 J J J最小时拟合最佳,而 J J J的导数为零时对应 J J J的一个极小值,这里就是它的最小值,得到
d ( J ) / d ( θ ) = 0 X T X θ − X T Y = 0 X T X θ = X T Y θ = ( X T X ) − 1 X T Y \begin{aligned} d(J)/d(θ)& = 0\\ X^TXθ - X^TY& = 0\\ X^TXθ& = X^TY\\ θ& = (X^TX)^{-1}X^TY\\ \end{aligned} d(J)/d(θ)XTXθ−XTYXTXθθ=0=0=XTY=(XTX)−1XTY
这样就得到了正规方程 θ = ( X T X ) − 1 X T Y θ=(X^TX)^{-1}X^TY θ=(XTX)−1XTY,这里我们算算 θ θ θ的维度, ( X T X ) − 1 X T Y (X^TX)^{-1}X^TY (XTX)−1XTY得到 ( 2 × 5 × 5 × 2 × 2 × 5 × 5 × 1 ) = ( 2 × 1 ) (2\times5 \times 5\times2 \times 2\times5 \times 5\times1)=(2\times1) (2×5×5×2×2×5×5×1)=(2×1),可以看到这里的 θ θ θ就是一个 2 × 1 2\times1 2×1的向量,里面包含了所有参数的值,这里只有 a a a和 b b b,所以这里的 θ [ 0 ] = b θ[0]=b θ[0]=b,而 θ [ 1 ] = a θ[1]=a θ[1]=a
我们回到开头的那个问题,看看数据和数据的维度
th = np.zeros((2, 1)) # 这是θ
X = np.array(x).T
Y = np.array(y).reshape(5, 1)
print(th.shape)
print(X.shape)
print(Y.shape)
这里的输出是
(2, 1)
(5, 2)
(5, 1)
现在我们构造这个正规方程并且计算,在python-numpy中,np.dot()是矩阵相乘,np.linalg.inv()是求逆矩阵,现在输出看看
th = np.dot(np.dot(np.linalg.inv(np.dot(X.T, X)), X.T), Y)
print('a='+str(th[1])+' b='+str(th[0]))
结果为,也就是 y = 2 x + 2.96 y=2x+2.96 y=2x+2.96
a=[2.] b=[2.96]
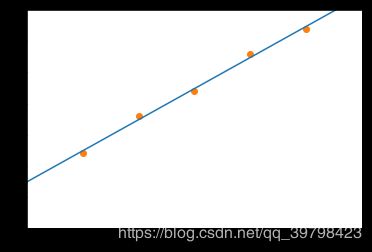
我们画个图看看
plt.scatter(x[1], y)
x2 = np.linspace(0, 6, 100)
fy = th[1]*x2+th[0]
plt.plot(x2, fy)
plt.xlim(0,6)
plt.ylim(0,14)
plt.show()
这个数据是按照 y = 2 x + 3 y=2x+3 y=2x+3构造的,这个结果和梯度下降的结果是差不多的,这就是矩阵求导最小二乘的解法
梯度下降和正规方程都适用于求最小二乘的一种方法,相同点在于它们都求了导数,目标都是最小化J;不同在于梯度下降需要设定学习率和需要多次迭代,而正规方程不需要。一般使用时,n<10000时且为线性模型我们可以用正规方程,当n>10000时由于逆矩阵的运算复杂度高,效率很低;而且正规方程只适用于线性模型,梯度下降法则可以适用各种模型,是更常用的做法