sklearn实战-----7.支持向量机SVM(上)
1 概述
支持向量机(SVM,也称为支持向量网络),是机器学习中获得关注最多的算法没有之一。它源于统计学习理论, 是我们除了集成算法之外,接触的第一个强学习器。它有多强呢?
从算法的功能来看,SVM几乎囊括了我们前六周讲解的所有算法的功能:
| 功能 | |
|---|---|
| 有监督学习 | 线性二分类与多分类(Linear Support Vector Classification) 非线性二分类与多分类(Support Vector Classification, SVC) 普通连续型变量的回归(Support Vector Regression) 概率型连续变量的回归(Bayesian SVM) |
| 无监督学习 | 支持向量聚类(Support Vector Clustering,SVC) 异常值检测(One-class SVM) |
| 半监督学习 | 转导支持向量机(Transductive Support Vector Machines,TSVM) |
从分类效力来讲,SVM在无论线性还是非线性分类中,都是明星般的存在:
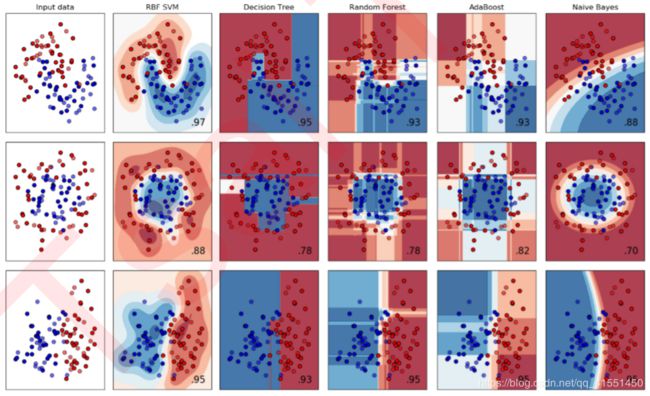
从实际应用来看,SVM在各种实际问题中都表现非常优秀。它在手写识别数字和人脸识别中应用广泛,在文本和超文本的分类中举足轻重,因为SVM可以大量减少标准归纳(standard inductive)和转换设置(transductive settings)中对标记训练实例的需求。同时,SVM也被用来执行图像的分类,并用于图像分割系统。实验结果表 明,在仅仅三到四轮相关反馈之后,SVM就能实现比传统的查询细化方案(query refinement schemes)高出一 大截的搜索精度。除此之外,生物学和许多其他科学都是SVM的青睐者,SVM现在已经广泛被用于蛋白质分类,现 在化合物分类的业界平均水平可以达到90%以上的准确率。在生物科学的尖端研究中,人们还使用支持向量机来识别用于模型预测的各种特征,以找出各种基因表现结果的影响因素。
从学术的角度来看,SVM是接近深度学习的机器学习算法。线性SVM可以看成是神经网络的单个神经元(虽然损 失函数与神经网络不同),非线性的SVM则与两层的神经网络相当,非线性的SVM中如果添加多个核函数,则可以 模仿多层的神经网络。而从数学的角度来看,SVM的数学原理是公认的对初学者来说难于上青天的水平,对于没有 数学基础和数学逻辑熏陶的人来说,探究SVM的数学原理本身宛如在知识的荒原上跋涉。
当然了,没有算法是完美的,比SVM强大的算法在集成学习和深度学习中还有很多很多。但不可否认,它是我们目 前为止接触到的最强大的算法。接下来的两周,我们将一起来探索SVM的神秘世界。
1.1 支持向量机分类器是如何工作的
支持向量机所作的事情其实非常容易理解。先来看看下面这一组数据的分布,这是一组两种标签的数据,两种标签 分别由圆和方块代表。支持向量机的分类方法,是在这组分布中找出一个超平面作为决策边界,使模型在数据上的 分类误差尽量接近于小,尤其是在未知数据集上的分类误差(泛化误差)尽量小。
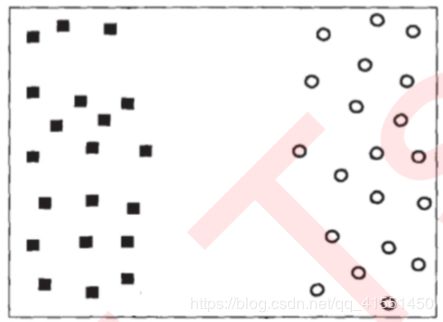
| 关键概念:超平面 |
|---|
| 在几何中,超平面是一个空间的子空间,它是维度比所在空间小一维的空间。 如果数据空间本身是三维的, 则其超平面是二维平面,而如果数据空间本身是二维的,则其超平面是一维的直线。 在二分类问题中,如果一个超平面能够将数据划分为两个集合,其中每个集合中包含单独的一个类别,我们就 说这个超平面是数据的“决策边界”。 |
决策边界一侧的所有点在分类为属于一个类,而另一侧的所有点分类属于另一个类。如果我们能够找出决策边界, 分类问题就可以变成探讨每个样本对于决策边界而言的相对位置。比如上面的数据分布,我们很容易就可以在方块 和圆的中间画出一条线,并让所有落在直线左边的样本被分类为方块,在直线右边的样本被分类为圆。如果把数据 当作我们的训练集,只要直线的一边只有一种类型的数据,就没有分类错误,我们的训练误差就会为0。 但是,对于一个数据集来说,让训练
误差为0的决策边界可以有无数条。
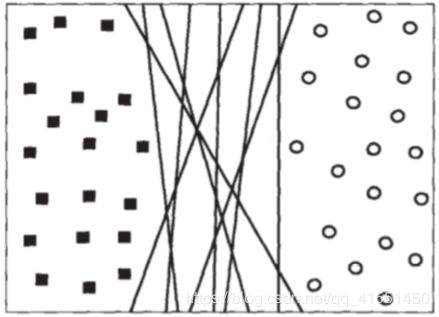
但在此基础上,我们无法保证这条决策边界在未知数据集(测试集)上的表现也会优秀。对于现有的数据集来说, 我们有 B 1 B_1 B1和 B 2 B_2 B2两条可能的决策边界。我们可以把决策边界 B 1 B_1 B1向两边平移,直到碰到离这条决策边界最近的方块和 圆圈后停下,形成两个新的超平面,分别是 b 11 b_{11} b11和 b 12 b_{12} b12 ,并且我们将原始的决策边界移动到 b 11 b_{11} b11和 b 12 b_{12} b12的中间,确保 B 1 B_1 B1 到 b 11 b_{11} b11和 b 12 b_{12} b12的距离相等。在 b 11 b_{11} b11和 b 12 b_{12} b12 中间的距离,叫做 这条决策边界的边际(margin),通常记作 d d d。
为了简便,我们称 b 11 b_{11} b11和 b 12 b_{12} b12为“虚线超平面”,在其他博客或教材中可能有着其他的称呼,但大家知道是这两个超平 面是由原来的决策边界向两边移动,直到碰到距离原来的决策边界最近的样本后停下而形成的超平面就可以了。
对 B 2 B_2 B2也执行同样的操作,然后我们来对比一下两个决策边界。现在两条决策边界右边的数据都被判断为圆,左边 的数据都被判断为方块,两条决策边界在现在的数据集上的训练误差都是0,没有一个样本被分错
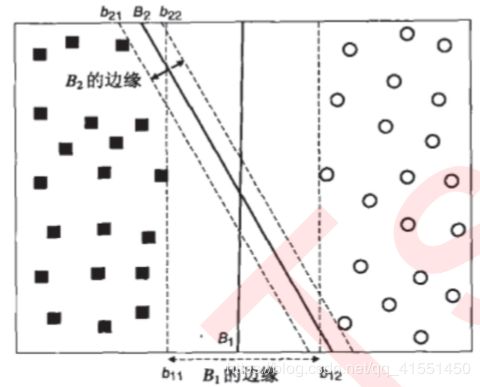
我们引入和原本的数据集相同分布的测试样本(红色所示),平面中的样本变多了,此时我们可以发现,对于 B 1 B_1 B1而言,依然没有一个样本被分错,这条决策边界上的泛化误差也是0。但是对于 B 2 B_2 B2而言,却有三个方块被误人类成 了圆,二有两个圆被误分类成了方块,这条决策边界上的泛化误差就远远大于 B 1 B_1 B1了。这个例子表现出,拥有更大 边际的决策边界在分类中的泛化误差更小,这一点可以由结构风险最小化定律来证明(SRM)。如果边际很小,则 任何轻微扰动都会对决策边界的分类产生很大的影响。边际很小的情况,是一种模型在训练集上表现很好,却在测 试集上表现糟糕的情况,所以会“过拟合”。所以我们在找寻决策边界的时候,希望边际越大越好。
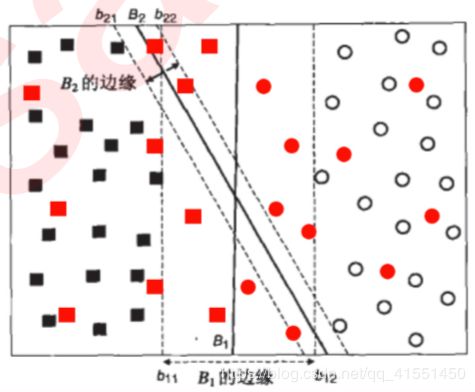
支持向量机,就是通过找出边际大的决策边界,来对数据进行分类的分类器。也因此,支持向量分类器又叫做最 大边际分类器。这个过程在二维平面中看起来十分简单,但将上述过程使用数学表达出来,就不是一件简单的事情 了。
1.2 支持向量机原理的三层理解
目标是"找出边际最大的决策边界",听起来是一个十分熟悉的表达,这是一个最优化问题,而最优化问题往往和损 失函数联系在一起。和逻辑回归中的过程一样,SVM也是通过最小化损失函数来求解一个用于后续模型使用的重要 信息:决策边界。
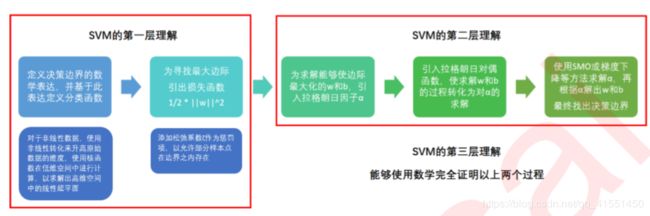
1.2 sklearn中的支持向量机
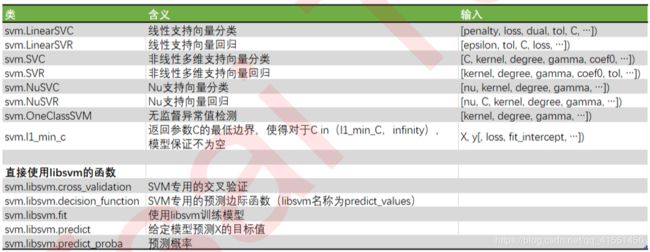
注意,除了特别表明是线性的两个类LinearSVC和LinearSVR之外,其他的所有类都是同时支持线性和非线性的。 NuSVC和NuSVC可以手动调节支持向量的数目,其他参数都与最常用的SVC和SVR一致。注意OneClassSVM是无监 督的类。
除了本身所带的类之外,sklearn还提供了直接调用libsvm库的几个函数。Libsvm是台湾大学林智仁(Lin Chih-Jen) 教授等人开发设计的一个简单、易于使用和快速有效的英文的SVM库,它提供了大量SVM的底层计算和参数选择, 也是sklearn的众多类背后所调用的库。目前,LIBSVM拥有C、Java、Matlab、Python、R等数十种语言版本,每 种语言版本都可以在libsvm的官网上进行下载:
https://www.csie.ntu.edu.tw/~cjlin/libsvm/
2 sklearn.svm.SVC
class s
klearn.svm.SVC(C=1.0, kernel=’rbf’, degree=3,
gamma=’auto_deprecated’, coef0=0.0, shrinking=True, probability=False,
tol=0.001, cache_size=200, class_weight=None, verbose=False,
max_iter=-1, decision_function_shape=’ovr’, random_state=None)
2.1 线性SVM用于分类的原理 2.1.1 线性SVM的损失函数详解
2.1.1 线性SVM的损失函数详解
要理解SVM的损失函数,我们先来定义决策边界。假设现在数据中总计有 N N N个训练样本,每个训练样本 i i i可以被表示为 ( x i , y i ) ( i = 1 , 2 , . . . . N ) (x_i,y_i)(i=1,2,....N) (xi,yi)(i=1,2,....N),其中 x i x_i xi是 ( x 1 i , x 2 i , . . . x n i ) T (x_{1i},x_{2i},...x_{ni})^T (x1i,x2i,...xni)T这样的一个特征向量,每个样本总共含有 n n n个特征。 二分类标签 y i y_i yi的取值是{-1, 1}。
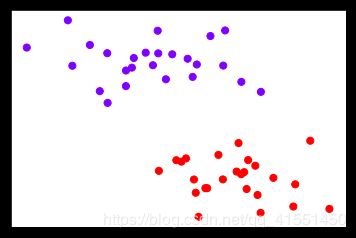
如果n等于2,则有 i = ( x 1 i , x 2 i , y i ) T i=(x_{1i},x_{2i},y_i)^T i=(x1i,x2i,yi)T ,分别由我们的特征向量和标签组成。此时我们可以在二维平面上,以 x 2 x_2 x2为 横坐标, x ! x_! x!为纵坐标, y y y为颜色,来可视化我们所有的N个样本:
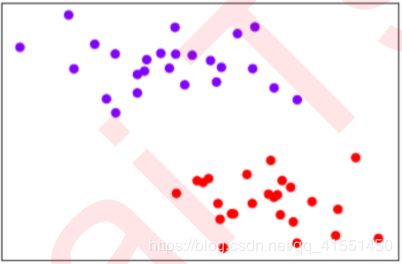
我们让所有紫色点的标签为1,红色点的标签为-1。我们要在这个数据集上寻找一个决策边界,在二维平面上,决 策边界(超平面)就是一条直线。二维平面上的任意一条线可以被表示为:
x 1 = a x 2 + b x_1=ax_2+b x1=ax2+b
我们将此表达式变换一下:
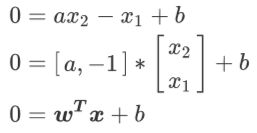
其中[a, -1]就是我们的参数向量 , 就是我们的特征向量, 是我们的截距。注意,这个表达式长得非常像我们线性回归的公式:
y ( x ) = θ T x + θ 0 y(x)=\theta ^Tx+\theta_0 y(x)=θTx+θ0
线性回归中等号的一边是标签,回归过后会拟合出一个标签,而决策边界的表达式中却没有标签的存在,全部是由 参数,特征和截距组成的一个式子,等号的一边是0。
在一组数据下,给定固定的 w w w和 b b b,这个式子就可以是一条固定直线,在 w w w和 b b b不确定的状况下,这个表达式 w T x + b = 0 w^Tx+b=0 wTx+b=0就可以代表平面上的任意一条直线。如果在 w w w和 b b b固定时,给定一个唯一的 x x x的取值,这个表达式就 可以表示一个固定的点。在SVM中,我们就使用这个表达式来表示我们的决策边界。我们的目标是求解能够让边际 最大化的决策边界,所以我们要求解参数向量 w w w和截距 b b b。
如果在决策边界上任意取两个点 , x a , x b x_a,x_b xa,xb,并带入决策边界的表达式,则有:
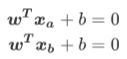
将两式相减,可以得到:
![]()
一个列向量的转至乘以另一个列向量,可以获得两个向量的点积(dot product),表示为 < w ⋅ ( x a − x b ) >

此时,我们有了我们的决策边界。任意一个紫色的点 就可以被表示为:
w ⋅ x p + b = p w \cdot x_p +b=p w⋅xp+b=p
由于紫色的点所代表的标签y是1,所以我们规定,p>0。同样的,对于任意一个红色的点 而言,我们可以将它表 示为:
w ⋅ x r + b = r w \cdot x_r +b=r w⋅xr+b=r
由于红色点所表示的标签y是-1,所以我们规定,r<0。由此,如果我们有新的测试数据 ,则的 标签就可以根 据以下式子来判定:
![]()
核心误区:p和r的符号
注意,在这里,p和r的符号是我们人为规定的。在一些博客或教材中,会认为p和r的符号是由原本的决策边界 上下移动得到。这是一种误解。
如果k和k’是由原本的决策边界平移得到的话,紫色的点在决策边界上方, w ⋅ x + b = 0 w \cdot x+b=0 w⋅x+b=0应该要向上平移,直线向上平移的话是增加截距,也就是说应该写作 w ⋅ x + b + 一 个 正 数 = 0 w \cdot x+b+一个正数=0 w⋅x+b+一个正数=0,那 p p p在等号的右边,怎么可能是一个大于0的数呢?同理,向下平移的话应该是截距减小,所以 也不可能是一个小于0的数。所以 p p p和 r r r的符号,不完全是平移的结果。
有人说,“直线以上的点带入直线为正,直线以下的点带入直线为负”是直线的性质,这又是另一种误解。假设我们有穿过圆点的直线 y = x y=x y=x,我们取点(x,y) = (0,1)这个在直线上的点为例,如果直线的表达式写作 y − x = 0 y-x=0 y−x=0,则点(0,1)带入后为正1,如果我们将直线的表达式写作 x − y = 0 x-y=0 x−y=0,则带入(0,1)后结果为-1。所以,一个点在直线的上方,究竟会返回什么样的符号,是跟直线的表达式的写法有关的,不是直线上的点都为 正,直线下的点都为负。
可能细心的小伙伴会发现,我们规定了 p p p和 r r r的符号与标签的符号一致,所以有人会说, 和 的符号,由所代表的点的标签的符号决定。这不是完全错误的,但这种说法无法解释,为什么我们就可以这样规定。并且,标 签可以不是{-1,1},可以是{0,1},可以是{1,2},两个标签之间并不需要是彼此的负数,标签的取值其实也是我 们规定的。
那 p p p和 r r r的符号,到底是依据什么来定的呢?数学中很多过程,都是可以取巧的,来看以下过程。记得我们的决 策边界如果写成矩阵,可以表示为:

紫色点 x p x_p xp毫无疑问是在决策边界的上方的,此时我将决策边界向上移动,形成一条过 x p x_p xp的直线。根据我们平移的 规则,直线向上平移,是在截距后加一个正数,则等号的右边是一个负数,假设这个数等于-3,则有:

可以注意到,我们的参数向量由[a,-1]变成了[-a,1], b b b变成了 − b -b −b,但参数向量依旧可以被表示成 w w w,只是它是原来 的负数了,截距依旧可以被表示成 b b b,只是如果它原来是正,它现在就是负数了,如果它原本就是负数,那它现在 就是正数了。在这个调整中,我们通过将向上平移时产生的负号放入了参数向量和截距当中,这不影响我们求解, 只不过我们求解出的参数向量和截距的符号变化了,但决策边界本身没有变化。所以我们依然可以使用原来的字母 来表示这些更新后的参数向量和截距。通过这种方法,我们让 w ⋅ x + b = p w \cdot x+b=p w⋅x+b=p中的p大于0。我们让p大于0的目的, 是为了它的符号能够与我们的标签的符号一致,都是为了后续计算和推导的简便。
| 为了推导和计算的简便,我们规定: |
|---|
| 标签是{-1,1} |
| 决策边界以上的点,标签都为正,并且通过调整 w w w和 b b b的符号,让这个点在 w ⋅ x + b w \cdot x+b w⋅x+b上得出的结果为正。 |
| 决策边界以下的点,标签都为负,并且通过调整 w w w和 b b b的符号,让这个点在 w ⋅ x + b w \cdot x+b w⋅x+b上得出的结果为负。 |
| 结论:决策边界以上的点都为正,以下的点都为负,是我们为了计算简便,而人为规定的。这种规定,不会影 响对参数向量 w w w和截距 b b b的求解。 |
有了这个理解,剩下的推导就简单多了。我们之前说过,决策边界的两边要有两个超平面,这两个超平面在二维空 间中就是两条平行线(就是我们的虚线超平面),而他们之间的距离就是我们的边际 d d d。而决策边界位于这两条线 的中间,所以这两条平行线必然是对称的。我们另这两条平行线被表示为:
w ⋅ x + b = k , w ⋅ x + b = − k w\cdot x+ b =k, \ w\cdot x+ b =-k w⋅x+b=k, w⋅x+b=−k
两个表达式同时除以k,则可以得到:
w ⋅ x + b = 1 , w ⋅ x + b = − 1 w\cdot x+ b =1, \ w\cdot x+ b =-1 w⋅x+b=1, w⋅x+b=−1
这就是我们平行于决策边界的两条线的表达式,表达式两边的1和-1分别表示了两条平行于决策边界的虚线到决策 边界的相对距离。此时,我们可以让这两条线分别过两类数据中距离我们的决策边界近的点,这些点就被称 为“支持向量”,而决策边界永远在这两条线的中间,所以可以被调整。我们令紫色类的点为 x p x_p xp,红色类的点为 x r x_r xr, 则我们可以得到:
w ⋅ x p + b = 1 , w ⋅ x r + b = − 1 w\cdot x_p+ b =1, \ w\cdot x_r+ b =-1 w⋅xp+b=1, w⋅xr+b=−1
两个式子相减,则有:
w ⋅ ( x p − x r ) = 2 w \cdot(x_p-x_r)=2 w⋅(xp−xr)=2
如下图所示, ( x p − x r ) (x_p-x_r) (xp−xr)可表示为两点之间的连线,而我们的边际 d d d是平行于 w w w的,所以我们现在,相当于是得到 了三角型中的斜边,并且知道一条直角边的方向。在线性代数中,我们有如下数学性质:
线性代数中模长的运用
向量b除以自身的模长 ∣ ∣ b ∣ ∣ ||b|| ∣∣b∣∣可以得到b方向上的单位向量。
向量a乘以向量b方向上的单位向量,可以得到向量a在向量b方向上的投影的长度
所以,我们另上述式子两边同时除以 ∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣ ,则可以得到:

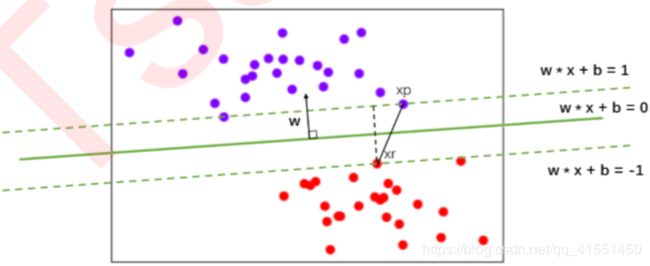
还记得我们想求什么吗?最大边界所对应的决策边界,那问题就简单了,要大化 d d d,就求解 w w w的小值。极值问 题可以相互转化,我们可以把求解 w w w的最小值转化为,求解以下函数的最小值:
f ( w ) = ∣ ∣ w ∣ ∣ 2 2 f(w)=\frac {||w||^2}{2} f(w)=2∣∣w∣∣2
只所以要在模长上加上平方,是因为模长的本质是一个距离,所以它是一个带根号的存在,我们对它取平方,是为了消除根号(其实模长的本质是向量 w w w的l2范式,还记得l2范式公式如何写的小伙伴必定豁然开朗)。
我们的两条虚线表示的超平面,是数据边缘所在的点。所以对于任意样本 i i i,我们可以把决策函数写作:

整理一下,我们可以把两个式子整合成:
![]()
在一部分教材中,这个式子被称为“函数间隔”。将函数间隔作为条件附加到我们的 f ( w ) f(w) f(w)上,我们就得到了SVM的损 失函数最初形态:
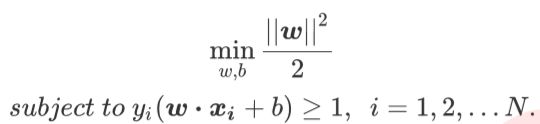
到这里,我们就完成了对SVM第一层理解的第一部分:线性SVM做二分类的损失函数。
2.1.2 函数间隔与几何间隔
重要定义:函数间隔与几何间隔
每一本机器学习的书或每一篇博客都可能有不同的原理讲解思路,在许多教材中,推导损失函数的过程与我们现在所说的不同。许多教材会先定义如下概念来辅助讲解: 对于给定的数据集T和超平面 ( w , b ) (w,b) (w,b) ,定义超平面 ( w , b ) (w,b) (w,b)关于样本点 ( x i , y i ) (x_i,y_i) (xi,yi)的函数间隔为:
γ i = y i ( w ⋅ x i + b ) \gamma_i=y_i(w \cdot x_i+b) γi=yi(w⋅xi+b)
这其实是我们的虚线超平面的表达式整理过后得到的式子。函数间隔可以表示分类预测的正确性以及确信度。 再在这个函数间隔的基础上除以 w w w的模长 ∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣来得到几何间隔:
γ i = y i ( w ∣ ∣ w ∣ ∣ x i + b ∣ ∣ w ∣ ∣ ) \gamma_i=y_i(\frac{w}{||w||}x_i+\frac{b}{||w||}) γi=yi(∣∣w∣∣wxi+∣∣w∣∣b)
几何间隔的本质其实是点 x i x_i xi到超平面(w,b),即到我们的决策边界的带符号的距离(signed distance)。
为什么几何间隔能够表示点到决策边界的距离?如果理解点到直线的距离公式,就可以很简单地理解这个式子。对于平面上的一个点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)和一条直线 a x + b y + c = 0 ax+by+c=0 ax+by+c=0,我们可以推导出点到直线的距离为:

其中[a,b]就是直线的参数向量 w w w,而 a 2 + b 2 \sqrt{a^2+b^2} a2+b2其实就是参数向量 w w w的模长 ∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣。而我们的几何间隔中, y i y_i yi的取值 是{-1, 1},所以并不影响整个表达式的大小,只影响方向。而 w x + b = 0 wx+b=0 wx+b=0是决策边界,所以直线带入 x i x_i xi后再除以参数向量的模长,就可以得到点 x i x_i xi到决策边界的距离。
- 点到之间的距离的公式推导
现在有直线 L 0 : a x + b y + c = 0 L_0:ax+by+c=0 L0:ax+by+c=0,在直线上任意处选取点 M ( x 0 , y 0 ) M(x_0,y_0) M(x0,y0),过点M画垂直于直线 L 0 L_0 L0的线 L 1 L_1 L1,两条线的交点为 N ( x n , y n ) N(x_n,y_n) N(xn,yn)。现在MN线段的长度就是点M到直线 L 0 L_0 L0的距离,在求解距离过程中,M点的坐标和直线 L 0 L_0 L0都是已知的,未知数是交点的坐标 N ( x n , y n ) N(x_n,y_n) N(xn,yn),于是我们将求解距离问题转化为求解交点的问题。

首先将 L 1 L_1 L1稍作变化,写作 y = − a b x − c b y=- \frac abx-\frac cb y=−bax−bc。开始证明:

求得点N的坐标后,线段MN的长度,即M到N的距离则可表示为:

证明完毕。
2.1.3 线性SVM的拉格朗日对偶函数和决策函数
有了我们的损失函数过后,我们就需要对损失函数进行求解。这个求解过程异常复杂,涉及到的数学的难度不是推 导损失函数的部分可比。并且,在sklearn当中,我们作为使用者完全无法干涉这个求解的过程。因此作为使用 sklearn的人,这部分属于进阶内容。如果实在对数学感到苦手,大家也可根据自己的需求选读。
我们之前得到了线性SVM损失函数的最初形态:

这个损失函数分为两部分:需要最小化的函数,以及参数求解后必须满足的约束条件。这是一个最优化问题。
2.1.3.1 将损失函数从初形态转换为拉格朗日乘数形态
- 为什么要进行转换?
我们的目标是求解让损失函数最小化的 w w w,但其实很容易看得出来,如果 ∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣ 为0, f ( w ) f(w) f(w) 必然最小了。但是, ∣ ∣ w ∣ ∣ = 0 ||w||=0 ∣∣w∣∣=0 其实是一个无效的值,原因有简单:首先,我们的决策边界是 w ⋅ x + b = 0 w \cdot x+b=0 w⋅x+b=0,如果 w w w为0,则这个向量里 包含的所有元素都为0,那就有b = 0这个唯一值。然而,如果b和 w w w 都为0,决策边界就不再是一条直线了,函数间隔 y i ( w ⋅ x i + b ) y_i(w \cdot x_i+b) yi(w⋅xi+b)就会为0,条件中的 y i ( w ⋅ x i + b ) ≥ 1 y_i(w \cdot x_i+b)\ge1 yi(w⋅xi+b)≥1就不可能实现,所以 w w w不可以是一个0向量。可见,单纯让 f ( w ) = ∣ ∣ w ∣ ∣ 2 2 f(w)=\frac{||w||^2}2 f(w)=2∣∣w∣∣2为0,是不能求解出合理的 w w w的,我们希望能够找出一种方式,能够让我们的条件 y i ( w ⋅ x i + b ) ≥ 1 y_i(w \cdot x_i+b)\ge1 yi(w⋅xi+b)≥1在计算中也被纳入考虑,一种业界认可的方法是使用拉格朗日乘数法(standard Lagrange multiplier method)
- 为什么可以进行转换?
我们的损失函数是二次的(quadratic),并且我们损失函数中的约束条件在参数w和b下是线性的,求解这样的损失 函数被称为“凸优化问题”(convex optimization problem)。拉格朗日乘数法正好可以用来解决凸优化问题,这种方 法也是业界常用的,用来解决带约束条件,尤其是带有不等式的约束条件的函数的数学方法。首先第一步,我们需 要使用拉格朗日乘数来将损失函数改写为考虑了约束条件的形式:
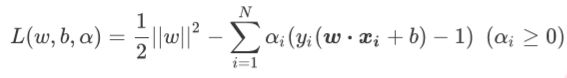
这是一个非常聪明而且巧妙的表达式,它被称为拉格朗日函数,其中 α i \alpha_i αi就叫做拉格朗日乘数。此时此刻,我们要求解的就不只有参数向量 w w w和截距 b b b了,我们也要求解拉格朗日乘数 α \alpha α ,而我们的 x i x_i xi和 y i y_i yi都是我们已知的特征矩阵和标 签。
- 怎样进行转换?
拉格朗日函数也分为两部分。第一部分和我们原始的损失函数一样,第二部分呈现了我们带有不等式的约束条件。 我们希望, L ( w , b , a ) L(w,b,a) L(w,b,a)不仅能够代表我们原有的损失函数 f ( w ) f(w) f(w)和约束条件,还能够表示我们想要最小化损失函数来 求解 w w w和 b b b的意图,所以我们要先以 α \alpha α为参数,求解 L ( w , b , a ) L(w,b,a) L(w,b,a)的最大值,再以 w w w和 b b b为参数,求解 L ( w , b , a ) L(w,b,a) L(w,b,a)的最小 值。因此,我们的目标可以写作:
![]()

2.1.3.2 将拉格朗日函数转换为拉格朗日对偶函数
- 为什么要进行转换?
要求极值,最简单的方法还是对参数求导后让一阶导数等于0。我们先来试试看对拉格朗日函数求极值,在这里我 们对参数向量 w w w和截距 b b b分别求偏导并且让他们等于0。这个求导过程比较简单:

由于两个求偏导结果中都带有未知的拉格朗日乘数 α i \alpha_i αi ,因此我们还是无法求解出 w w w和 b b b,我们必须想出一种方法来求解拉格朗日乘数 α i \alpha_i αi。幸运地是,拉格朗日函数可以被转换成一种只带有 α i \alpha_i αi,而不带有 w w w和 b b b的形式,这种形式被 称为拉格朗日对偶函数。在对偶函数下,我们就可以求解出拉格朗日乘数 α i \alpha_i αi,然后带入到上面推导出的(1)和(2)式 中来求解 w w w和 b b b 。
- 为什么能够进行转换?
- 怎样进行转换?
2.1.3.3 求解拉格朗日对偶函数极其后续过程
2.1.4 线性SVM决策过程的可视化
我们可以使用sklearn中的式子来为可视化我们的决策边界,支持向量,以及决策边界平行的两个超平面。
- 导入需要的模块
from sklearn.datasets import make_blobs
from sklearn.svm import SVC
import matplotlib.pyplot as plt
import numpy as np
- 实例化数据集,可视化数据集
X,y = make_blobs(n_samples=50, centers=2, random_state=0,cluster_std=0.6)
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")#rainbow彩虹色
plt.xticks([])
plt.yticks([])
plt.show()
- 画决策边界:理解函数contour
matplotlib.axes.Axes.contour([X, Y,] Z, [levels], **kwargs)
Contour是我们专门用来绘制等高线的函数。等高线,本质上是在二维图像上表现三维图像的一种形式,其中两维 X和Y是两条坐标轴上的取值,而Z表示高度。Contour就是将由X和Y构成平面上的所有点中,高度一致的点连接成 线段的函数,在同一条等高线上的点一定具有相同的Z值。我们可以利用这个性质来绘制我们的决策边界。
| 参数 | 含义 |
|---|---|
| X,Y | 选填。两维平面上所有的点的横纵坐标取值,一般要求是二维结构并且形状需要与Z相同,往往通 过numpy.meshgrid()这样的函数来创建。如果X和Y都是一维,则Z的结构必须为(len(Y), len(X))。 如果不填写,则默认X = range(Z.shape[1]),Y = range(Z.shape[0])。 |
| Z | 必填。平面上所有的点所对应的高度。 |
| levels | 可不填,不填默认显示所有的等高线,填写用于确定等高线的数量和位置。如果填写整数n,则显 示n个数据区间,即绘制n+1条等高线。水平高度自动选择。如果填写的是数组或列表,则在指定 的高度级别绘制等高线。列表或数组中的值必须按递增顺序排列。 |
回忆一下,我们的决策边界是 w ⋅ x + b = 0 w\cdot x+b=0 w⋅x+b=0,并在决策边界的两边找出两个超平面,使得超平面到决策边界的相 对距离为1。那其实,我们只需要在我们的样本构成的平面上,把所有到决策边界的距离为0的点相连,就是我们的 决策边界,而把所有到决策边界的相对距离为1的点相连,就是我们的两个平行于决策边界的超平面了。此时,我 们的Z就是平面上的任意点到达超平面的距离。
那首先,我们需要获取样本构成的平面,作为一个对象
#首先要有散点图
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
ax = plt.gca() #获取当前的子图,如果不存在,则创建新的子图
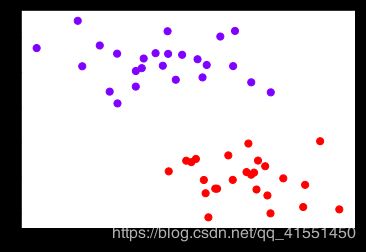
有了这个平面,我们需要在平面上制作一个足够细的网格,来代表我们“平面上的所有点”。
- 画决策边界:制作网格,理解函数meshgrid
#获取平面上两条坐标轴的最大值和最小值
xlim = ax.get_xlim()
ylim = ax.get_ylim()
#在最大值和最小值之间形成30个规律的数据
axisx = np.linspace(xlim[0],xlim[1],30)
axisy = np.linspace(ylim[0],ylim[1],30)
axisy,axisx = np.meshgrid(axisy,axisx)
#我们将使用这里形成的二维数组作为我们contour函数中的X和Y
#使用meshgrid函数将两个一维向量转换为特征矩阵
#核心是将两个特征向量广播,以便获取y.shape * x.shape这么多个坐标点的横坐标和纵坐标
xy = np.vstack([axisx.ravel(), axisy.ravel()]).T
#其中ravel()是降维函数,vstack能够将多个结构一致的一维数组按行堆叠起来
#xy就是已经形成的网格,它是遍布在整个画布上的密集的点
plt.scatter(xy[:,0],xy[:,1],s=1,cmap="rainbow")
#理解函数meshgrid和vstack的作用
a = np.array([1,2,3])
b = np.array([7,8])
#两两组合,会得到多少个坐标?
#答案是6个,分别是 (1,7),(2,7),(3,7),(1,8),(2,8),(3,8)
v1,v2 = np.meshgrid(a,b)
v1
v2
v = np.vstack([v1.ravel(), v2.ravel()]).T

有了网格后,我们需要计算网格所代表的“平面上所有的点”到我们的决策边界的距离。所以我们需要我们的模型和
决策边界。
- 建模,计算决策边界并找出网格上每个点到决策边界的距离
#建模,通过fit计算出对应的决策边界
clf = SVC(kernel = "linear").fit(X,y)#计算出对应的决策边界
Z = clf.decision_function(xy).reshape(axisx.shape)
#重要接口decision_function,返回每个输入的样本所对应的到决策边界的距离
#然后再将这个距离转换为axisx的结构,这是由于画图的函数contour要求Z的结构必须与X和Y保持一致
#首先要有散点图
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
ax = plt.gca() #获取当前的子图,如果不存在,则创建新的子图
#画决策边界和平行于决策边界的超平面
ax.contour(axisx,axisy,Z
,colors="k"
,levels=[-1,0,1] #画三条等高线,分别是Z为-1,Z为0和Z为1的三条线
,alpha=0.5#透明度
,linestyles=["--","-","--"])
ax.set_xlim(xlim)#设置x轴取值
ax.set_ylim(ylim)
(-0.43660961990940284, 5.772756283035797)

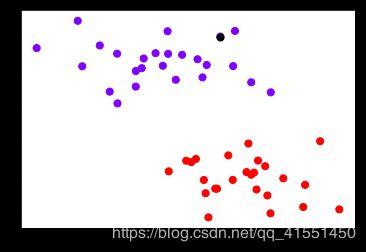
#记得Z的本质么?是输入的样本到决策边界的距离,而contour函数中的level其实是输入了这个距离
#让我们用一个点来试试看
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
plt.scatter(X[10,0],X[10,1],c="black",s=50,cmap="rainbow")
clf.decision_function(X[10].reshape(1,2))
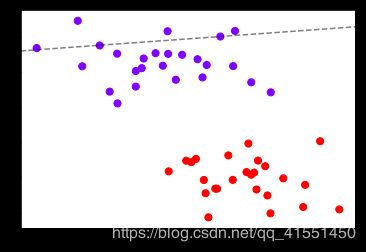
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
ax = plt.gca()
ax.contour(axisx,axisy,Z
,colors="k"
,levels=[-3.33917354]
,alpha=0.5
,linestyles=["--"])
- 将绘图过程包装成函数
#将上述过程包装成函数:
def plot_svc_decision_function(model,ax=None):
if ax is None:
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
x = np.linspace(xlim[0],xlim[1],30)
y = np.linspace(ylim[0],ylim[1],30)
Y,X = np.meshgrid(y,x)
xy = np.vstack([X.ravel(), Y.ravel()]).T
P = model.decision_function(xy).reshape(X.shape)
ax.contour(X, Y, P,colors="k",levels=[-1,0,1],alpha=0.5,linestyles=["--","-","--"])
ax.set_xlim(xlim)
ax.set_ylim(ylim)
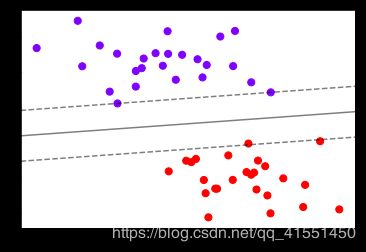
#则整个绘图过程可以写作:
clf = SVC(kernel = "linear").fit(X,y)
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
plot_svc_decision_function(clf)
- 探索建好的模型
clf.predict(X)
#根据决策边界,对X中的样本进行分类,返回的结构为n_samples
clf.score(X,y)
#返回给定测试数据和标签的平均准确度
clf.support_vectors_
#返回支持向量坐标
clf.n_support_#array([2, 1])
#返回每个类中支持向量的个数
- 推广到非线性情况
我们之前所讲解的原理,以及绘图的过程,都是基于数据本身是线性可分的情况。如果把数据推广到非线性数据,
比如说环形数据上呢?
from sklearn.datasets import make_circles
X,y = make_circles(100, factor=0.1, noise=.1)
X.shape
y.shape
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
plt.show()

试试看用我们已经定义的函数来划分这个数据的决策边界:
0.68

明显,现在线性SVM已经不适合于我们的状况了,我们无法找出一条直线来划分我们的数据集,让直线的两边分别是两种类别。这个时候,如果我们能够在原本的X和y的基础上,添加一个维度r,变成三维,我们可视化这个数据,来看看添加维度让我们的数据如何变化。
- 为非线性数据增加维度并绘制3D图像
#定义一个由x计算出来的新维度r
r = np.exp(-(X**2).sum(1))
rlim = np.linspace(min(r),max(r),100)
from mpl_toolkits import mplot3d
#定义一个绘制三维图像的函数
#elev表示上下旋转的角度
#azim表示平行旋转的角度
def plot_3D(elev=30,azim=30,X=X,y=y):
ax = plt.subplot(projection="3d")
ax.scatter3D(X[:,0],X[:,1],r,c=y,s=50,cmap='rainbow')
ax.view_init(elev=elev,azim=azim)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("r")
plt.show()
plot_3D()
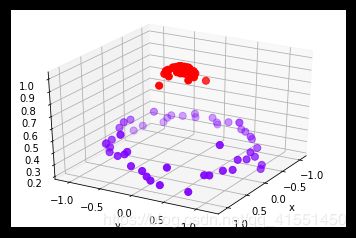
可以看见,此时此刻我们的数据明显是线性可分的了:我们可以使用一个平面来将数据完全分开,并使平面的上方的所有数据点为一类,平面下方的所有数据点为另一类。
- 将上述过程放到Jupyter Notebook中运行
#如果放到jupyter notebook中运行
from sklearn.svm import SVC
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_circles
X,y = make_circles(100, factor=0.1, noise=.1)
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
def plot_svc_decision_function(model,ax=None):
if ax is None:
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
x = np.linspace(xlim[0],xlim[1],30)
y = np.linspace(ylim[0],ylim[1],30)
Y,X = np.meshgrid(y,x)
xy = np.vstack([X.ravel(), Y.ravel()]).T
P = model.decision_function(xy).reshape(X.shape)
ax.contour(X, Y, P,colors="k",levels=[-1,0,1],alpha=0.5,linestyles=["--","-","--"])
ax.set_xlim(xlim)
ax.set_ylim(ylim)
clf = SVC(kernel = "linear").fit(X,y)
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
plot_svc_decision_function(clf)
r = np.exp(-(X**2).sum(1))
rlim = np.linspace(min(r),max(r),0.2)
from mpl_toolkits import mplot3d
def plot_3D(elev=30,azim=30,X=X,y=y):
ax = plt.subplot(projection="3d")
ax.scatter3D(X[:,0],X[:,1],r,c=y,s=50,cmap='rainbow')
ax.view_init(elev=elev,azim=azim)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("r")
plt.show()
from ipywidgets import interact,fixed
interact(plot_3D,elev=[0,30,60,90],azip=(-180,180),X=fixed(X),y=fixed(y))
plt.show()
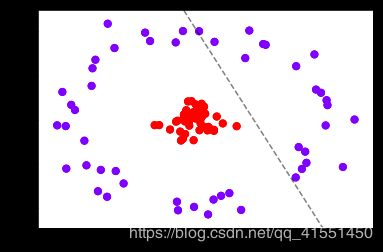
此时我们的数据在三维空间中,我们的超平面就是一个二维平面。明显我们可以用一个平面将两类数据隔开,这个平面就是我们的决策边界了。我们刚才做的,计算r,并将r作为数据的第三维度来将数据升维的过程,被称为“核变换”,即是将数据投影到高维空间中,以寻找能够将数据完美分割的超平面,即是说寻找能够让数据线性可分的高维空间。为了详细解释这个过程,我们需要引入SVM中的核心概念:核函数。
2.2 非线性SVM与核函数
2.2.1 SVC在非线性数据上的推广
为了能够找出非线性数据的线性决策边界,我们需要将数据从原始的空间 x x x投射到新空间 ϕ ( x ) \phi(x) ϕ(x)中。 ϕ \phi ϕ是一个映射函数,它代表了某种非线性的变换,如同我们之前所做过的使用r来升维一样,这种非线性变换看起来是一种非常有效的方式。使用这种变换,线性SVM的原理可以被很容易推广到非线性情况下,其推导过程和逻辑都与线性SVM一模一样,只不过在定义决策边界之前,我们必须先对数据进行升维度,即将原始的 转换成 ϕ ( x ) \phi(x) ϕ(x) 。
如此,非线性SVM的损失函数的初始形态为:

同理,非线性SVM的拉格朗日函数和拉格朗日对偶函数也可得:
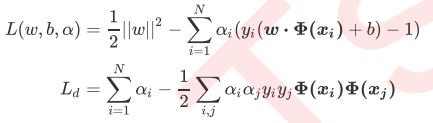
使用同样的推导方式,让拉格朗日函数满足KKT条件,并在拉格朗日函数上对每个参数求导,经过和线性SVM相同的变换后,就可以得到拉格朗日对偶函数。同样使用梯度下降或SMO等方式对 α \alpha α进行求解,最后可以求得决策边界,并得到最终的决策函数:
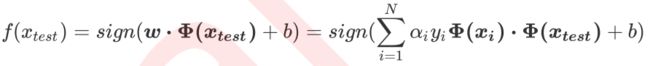
2.2.2 重要参数kernel
这种变换非常巧妙,但也带有一些实现问题。 首先,我们可能不清楚应该什么样的数据应该使用什么类型的映射函数来确保可以在变换空间中找出线性决策边界。极端情况下,数据可能会被映射到无限维度的空间中,这种高维空间可能不是那么友好,维度越多,推导和计算的难度都会随之暴增。其次,即使已知适当的映射函数,我们想要计算类似于 ϕ ( x i ) ⋅ ϕ ( x t e s t ) \phi(x_i)\cdot \phi(x_{test}) ϕ(xi)⋅ϕ(xtest)这样的点积,计算量可能会无比巨大,要找出超平面所付出的代价是非常昂贵的。
| 关键概念:核函数 |
|---|
| 而解决这些问题的数学方式,叫做“核技巧”(Kernel Trick),是一种能够使用数据原始空间中的向量计算来表示升维后的空间中的点积结果的数学方式。具体表现为, K ( u , v ) = ϕ ( u ) ⋅ ϕ ( v ) K(u,v)=\phi(u)\cdot \phi(v) K(u,v)=ϕ(u)⋅ϕ(v) 。而这个原始空间中的点积函数 K ( u , v ) K(u,v) K(u,v),就被叫做“核函数”(Kernel Function)。 |
核函数能够帮助我们解决三个问题:
第一,有了核函数之后,我们无需去担心 ϕ \phi ϕ 究竟应该是什么样,因为非线性SVM中的核函数都是正定核函数(positive definite kernel functions),他们都满足美世定律(Mercer’s theorem),确保了高维空间中任意两个向量的点积一定可以被低维空间中的这两个向量的某种计算来表示(多数时候是点积的某种变换)。
第二,使用核函数计算低维度中的向量关系比计算原本的 ϕ ( x i ) ⋅ ϕ ( x t e s t ) \phi(x_i)\cdot \phi(x_{test}) ϕ(xi)⋅ϕ(xtest)要简单太多了。
第三,因为计算是在原始空间中进行,所以避免了维度诅咒的问题。
选用不同的核函数,就可以解决不同数据分布下的寻找超平面问题。在SVC中,这个功能由参数“kernel”和一系列与核函数相关的参数来进行控制。之前的代码中我们一直使用这个参数并输入"linear",但却没有给大家详细讲解,也是因为如果不先理解核函数本身,很难说明这个参数到底在做什么。参数“kernel"在sklearn中可选以下几种选项:

可以看出,除了选项"linear"之外,其他核函数都可以处理非线性问题。多项式核函数有次数d,当d为1的时候它 就是再处理线性问题,当d为更高次项的时候它就是在处理非线性问题。我们之前画图时使用的是选项“linear",自 然不能处理环形数据这样非线性的状况。而刚才我们使用的计算r的方法,其实是高斯径向基核函数所对应的功 能,在参数”kernel“中输入”rbf“就可以使用这种核函数。我们来看看模型找出的决策边界时什么样:
clf = SVC(kernel = "rbf").fit(X,y)
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
plot_svc_decision_function(clf)
可以看到,决策边界被完美地找了出来。
2.2.3 探索核函数在不同数据集上的表现
除了"linear"以外的核函数都能够处理非线性情况,那究竟什么时候选择哪一个核函数呢?遗憾的是,关于核函数 在不同数据集上的研究甚少,谷歌学术上的论文中也没有几篇是研究核函数在SVM中的运用的,更多的是关于核函 数在深度学习,神经网络中如何使用。在sklearn中,也没有提供任何关于如何选取核函数的信息。
但无论如何,我们还是可以通过在不同的核函数中循环去找寻最佳的核函数来对核函数进行一个选取。接下来我们 就通过一个例子,来探索一下不同数据集上核函数的表现。我们现在有一系列线性或非线性可分的数据,我们希望 通过绘制SVC在不同核函数下的决策边界并计算SVC在不同核函数下分类准确率来观察核函数的效用。
- 导入所需要的库和模块
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn import svm#from sklearn.svm import SVC 两者都可以
from sklearn.datasets import make_circles, make_moons, make_blobs,make_classification
- 创建数据集,定义核函数的选择
n_samples = 100
datasets = [
make_moons(n_samples=n_samples, noise=0.2, random_state=0),
make_circles(n_samples=n_samples, noise=0.2, factor=0.5, random_state=1),
make_blobs(n_samples=n_samples, centers=2, random_state=5),#分簇的数据集
make_classification(n_samples=n_samples,n_features = 2,n_informative=2,n_redundant=0, random_state=5)
#n_features:特征数,n_informative:带信息的特征数,n_redundant:不带信息的特征数
]
Kernel = ["linear","poly","rbf","sigmoid"]
#四个数据集分别是什么样子呢?
for X,Y in datasets:
plt.figure(figsize=(5,4))
plt.scatter(X[:,0],X[:,1],c=Y,s=50,cmap="rainbow")

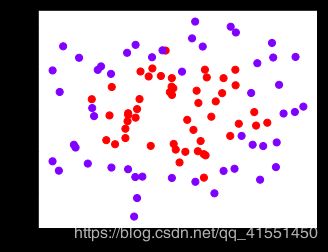
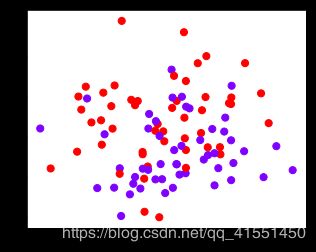

我们总共有四个数据集,四种核函数,我们希望观察每种数据集下每个核函数的表现。以核函数为列,以图像分布为行,我们总共需要16个子图来展示分类结果。而同时,我们还希望观察图像本身的状况,所以我们总共需要20个子图,其中第一列是原始图像分布,后面四列分别是这种分布下不同核函数的表现。
- 构建子图
nrows=len(datasets)
ncols=len(Kernel) + 1
fig, axes = plt.subplots(nrows, ncols,figsize=(20,16))
- 开始进行子图循环
nrows=len(datasets)
ncols=len(Kernel) + 1
fig, axes = plt.subplots(nrows, ncols,figsize=(20,16))
#第一层循环:在不同的数据集中循环
for ds_cnt, (X,Y) in enumerate(datasets):
#在图像中的第一列,放置原数据的分布
ax = axes[ds_cnt, 0]
if ds_cnt == 0:
ax.set_title("Input data")
ax.scatter(X[:, 0], X[:, 1], c=Y, zorder=10, cmap=plt.cm.Paired,edgecolors='k')
ax.set_xticks(())
ax.set_yticks(())
#第二层循环:在不同的核函数中循环
#从图像的第二列开始,一个个填充分类结果
for est_idx, kernel in enumerate(Kernel):
#定义子图位置
ax = axes[ds_cnt, est_idx + 1]
#建模
clf = svm.SVC(kernel=kernel, gamma=2).fit(X, Y)
score = clf.score(X, Y)
#绘制图像本身分布的散点图
ax.scatter(X[:, 0], X[:, 1], c=Y
,zorder=10
,cmap=plt.cm.Paired,edgecolors='k')
#绘制支持向量
ax.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=50,
facecolors='none', zorder=10, edgecolors='k')# facecolors='none':透明的
#绘制决策边界
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
#np.mgrid,合并了我们之前使用的np.linspace和np.meshgrid的用法
#一次性使用最大值和最小值来生成网格
#表示为[起始值:结束值:步长]
#如果步长是复数,则其整数部分就是起始值和结束值之间创建的点的数量,并且结束值被包含在内
XX, YY = np.mgrid[x_min:x_max:200j, y_min:y_max:200j]
#np.c_,类似于np.vstack的功能
Z = clf.decision_function(np.c_[XX.ravel(), YY.ravel()]).reshape(XX.shape)
#填充等高线不同区域的颜色
ax.pcolormesh(XX, YY, Z > 0, cmap=plt.cm.Paired)
#绘制等高线
ax.contour(XX, YY, Z, colors=['k', 'k', 'k'], linestyles=['--', '-', '--'],
levels=[-1, 0, 1])
#设定坐标轴为不显示
ax.set_xticks(())
ax.set_yticks(())
#将标题放在第一行的顶上
if ds_cnt == 0:
ax.set_title(kernel)
#为每张图添加分类的分数
ax.text(0.95, 0.06, ('%.2f' % score).lstrip('0')
, size=15
, bbox=dict(boxstyle='round', alpha=0.8, facecolor='white')
#为分数添加一个白色的格子作为底色
, transform=ax.transAxes #确定文字所对应的坐标轴,就是ax子图的坐标轴本身
, horizontalalignment='right' #位于坐标轴的什么方向
)
plt.tight_layout()
plt.show()
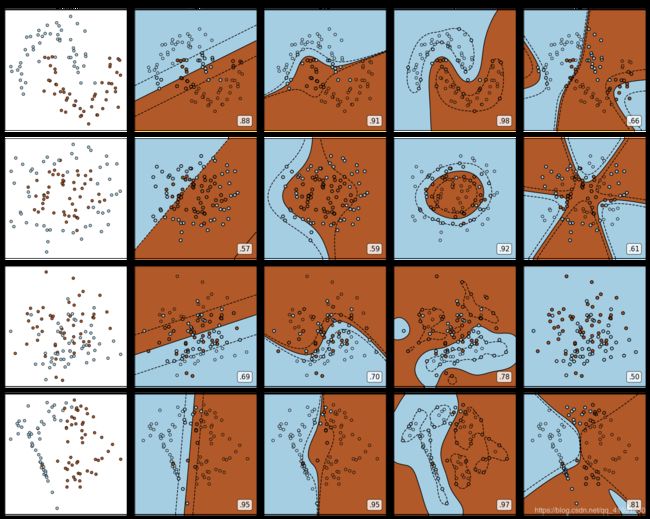
可以观察到,线性核函数和多项式核函数在非线性数据上表现会浮动,如果数据相对线性可分,则表现不错,如果是像环形数据那样彻底不可分的,则表现糟糕。在线性数据集上,线性核函数和多项式核函数即便有扰动项也可以表现不错,可见多项式核函数是虽然也可以处理非线性情况,但更偏向于线性的功能。
Sigmoid核函数就比较尴尬了,它在非线性数据上强于两个线性核函数,但效果明显不如rbf,它在线性数据上完全
比不上线性的核函数们,对扰动项的抵抗也比较弱,所以它功能比较弱小,很少被用到。
rbf,高斯径向基核函数基本在任何数据集上都表现不错,属于比较万能的核函数。我个人的经验是,无论如何先试试看高斯径向基核函数,它适用于核转换到很高的空间的情况,在各种情况下往往效果都很不错,如果rbf效果不好,那我们再试试看其他的核函数。另外,多项式核函数多被用于图像处理之中。
2.2.4 探索核函数的优势和缺陷
看起来,除了Sigmoid核函数,其他核函数效果都还不错。但其实rbf和poly都有自己的弊端,我们使用乳腺癌数据集作为例子来展示一下:
from sklearn.datasets import load_breast_cancer
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import numpy as np
from time import time
import datetime
data = load_breast_cancer()
X = data.data
y = data.target
X.shape
np.unique(y)
plt.scatter(X[:,0],X[:,1],c=y)
plt.show()
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y,test_size=0.3,random_state=420)
Kernel = ["linear","poly","rbf","sigmoid"]
for kernel in Kernel:
time0 = time()
clf= SVC(kernel = kernel
, gamma="auto"
# , degree = 1
, cache_size=10000#使用计算的内存,单位是MB,默认是200MB
).fit(Xtrain,Ytrain)
print("The accuracy under kernel %s is %f" % (kernel,clf.score(Xtest,Ytest)))
print(time()-time0)
然后我们发现,怎么跑都跑不出来。模型一直停留在线性核函数之后,就没有再打印结果了。这证明,多项式核函数此时此刻要消耗大量的时间,运算非常的缓慢。让我们在循环中去掉多项式核函数,再试试看能否跑出结果:
Kernel = ["linear","rbf","sigmoid"]
for kernel in Kernel:
time0 = time()
clf= SVC(kernel = kernel
, gamma="auto"
# , degree = 1
, cache_size=5000
).fit(Xtrain,Ytrain)
print("The accuracy under kernel %s is %f" % (kernel,clf.score(Xtest,Ytest)))
print(time()-time0)
The accuracy under kernel linear is 0.929825
0.795527458190918
The accuracy under kernel rbf is 0.596491
0.06104254722595215
The accuracy under kernel sigmoid is 0.596491
0.008005142211914062
我们可以有两个发现。首先,乳腺癌数据集是一个线性数据集,线性核函数跑出来的效果很好。rbf和sigmoid两个擅长非线性的数据从效果上来看完全不可用。其次,线性核函数的运行速度远远不如非线性的两个核函数。
如果数据是线性的,那如果我们把degree参数调整为1,多项式核函数应该也可以得到不错的结果:
Kernel = ["linear","poly","rbf","sigmoid"]
for kernel in Kernel:
time0 = time()
clf= SVC(kernel = kernel
, gamma="auto"
, degree = 1
, cache_size=5000
).fit(Xtrain,Ytrain)
print("The accuracy under kernel %s is %f" % (kernel,clf.score(Xtest,Ytest)))
print(time()-time0)
The accuracy under kernel linear is 0.929825
0.8025338649749756
The accuracy under kernel poly is 0.923977
0.14710068702697754
The accuracy under kernel rbf is 0.596491
0.06003713607788086
The accuracy under kernel sigmoid is 0.596491
0.011008739471435547
多项式核函数的运行速度立刻加快了,并且精度也提升到了接近线性核函数的水平,可喜可贺。但是,我们之前的实验中,我们了解说,rbf在线性数据上也可以表现得非常好,那在这里,为什么跑出来的结果如此糟糕呢?
其实,这里真正的问题是数据的量纲问题。回忆一下我们如何求解决策边界,如何判断点是否在决策边界的一边?是靠计算”距离“,虽然我们不能说SVM是完全的距离类模型,但是它严重受到数据量纲的影响。让我们来探索一下乳腺癌数据集的量纲:
import pandas as pd
data = pd.DataFrame(X)
data.describe([0.01,0.05,0.1,0.25,0.5,0.75,0.9,0.99]).T#描述性统计
#从mean列和std列可以看出严重的量纲不统一
#从1%的数据和最小值相对比,90%的数据和最大值相对比,查看是否是正态分布或偏态分布,如果差的太多就是偏态分布,谁大方向就偏向谁
#可以发现数据大的特征存在偏态问题
#这个时候就需要对数据进行标准化
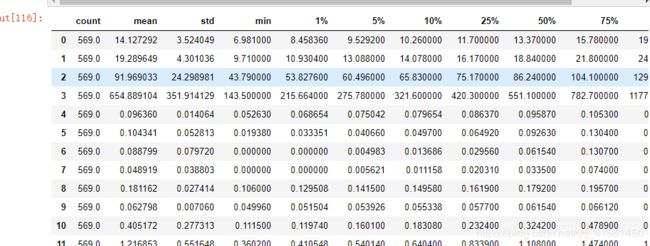
一眼望去,果然数据存在严重的量纲不一的问题。我们来使用数据预处理中的标准化的类,对数据进行标准化:
from sklearn.preprocessing import StandardScaler
X = StandardScaler().fit_transform(X)#将数据转化为0,1正态分布
data = pd.DataFrame(X)
data.describe([0.01,0.05,0.1,0.25,0.5,0.75,0.9,0.99]).T#均值很接近,方差为1了

标准化完毕后,再次让SVC在核函数中遍历,此时我们把degree的数值设定为1,观察各个核函数在去量纲后的数据上的表现:
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y,test_size=0.3,random_state=420)
Kernel = ["linear","poly","rbf","sigmoid"]
for kernel in Kernel:
time0 = time()
clf= SVC(kernel = kernel
, gamma="auto"
, degree = 1
, cache_size=5000
).fit(Xtrain,Ytrain)
print("The accuracy under kernel %s is %f" % (kernel,clf.score(Xtest,Ytest)))
print(time()-time0)
The accuracy under kernel linear is 0.976608
0.01501321792602539
The accuracy under kernel poly is 0.964912
0.006003141403198242
The accuracy under kernel rbf is 0.970760
0.011005401611328125
The accuracy under kernel sigmoid is 0.953216
0.0060024261474609375
量纲统一之后,可以观察到,所有核函数的运算时间都大大地减少了,尤其是对于线性核来说,而多项式核函数居然变成了计算最快的。其次,rbf表现出了非常优秀的结果。经过我们的探索,我们可以得到的结论是:
- 线性核,尤其是多项式核函数在高次项时计算非常缓慢
- rbf和多项式核函数都不擅长处理量纲不统一的数据集
幸运的是,这两个缺点都可以由数据无量纲化来解决。因此,SVM执行之前,非常推荐先进行数据的无量纲化!到了这一步,我们是否已经完成建模了呢?虽然线性核函数的效果是最好的,但它是没有核函数相关参数可以调整的,rbf和多项式却还有着可以调整的相关参数,接下来我们就来看看这些参数。
2.2.5 选取与核函数相关的参数:degree & gamma & coef0
在知道如何选取核函数后,我们还要观察一下除了kernel之外的核函数相关的参数。对于线性核函数,"kernel"是唯一能够影响它的参数,但是对于其他三种非线性核函数,他们还受到参数gamma,degree以及coef0的影响。参数gamma就是表达式中的 γ \gamma γ,degree就是多项式核函数的次数 d d d,参数coef0就是常数项 r r r。其中,高斯径向基核函数受到gamma的影响,而多项式核函数受到全部三个参数的影响。
| 参数 | 含义 |
|---|---|
| degree | 整数,可不填,默认3。 多项式核函数的次数(‘poly’),如果核函数没有选择"poly",这个参数会被忽略 |
| gamma | 浮点数,可不填,默认“auto"。核函数的系数,仅在参数Kernel的选项为”rbf",“poly"和"sigmoid”的时候有效;输入“auto”,自动使用1/(n_features)作为gamma的取值;输入"scale",则使用1/(n_features * X.std())作为gamma的取值;输入"auto_deprecated",则表示没有传递明确的gamma值(不推荐使用) |
| coef0 | 浮点数,可不填,默认=0.0。核函数中的常数项,它只在参数kernel为’poly’和’sigmoid’的时候有效 |
但从核函数的公式来看,我们其实很难去界定具体每个参数如何影响了SVM的表现。当gamma的符号变化,或者degree的大小变化时,核函数本身甚至都不是永远单调的。所以如果我们想要彻底地理解这三个参数,我们要先推导出它们如何影响核函数地变化,再找出核函数的变化如何影响了我们的预测函数(可能改变我们的核变化所在的维度),再判断出决策边界随着预测函数的改变发生了怎样的变化。无论是从数学的角度来说还是从实践的角度来说,这个过程太复杂也太低效。所以,我们往往避免去真正探究这些参数如何影响了我们的核函数,而直接使用学习曲线或者网格搜索来帮助我们查找最佳的参数组合。
对于高斯径向基核函数,调整gamma的方式其实比较容易,那就是画学习曲线。我们来试试看高斯径向基核函数rbf的参数gamma在乳腺癌数据集上的表现:
score = []
gamma_range = np.logspace(-10, 1, 50) #返回在对数刻度上均匀间隔的数字
for i in gamma_range:
clf = SVC(kernel="rbf",gamma = i,cache_size=5000).fit(Xtrain,Ytrain)
score.append(clf.score(Xtest,Ytest))
print(max(score), gamma_range[score.index(max(score))])
plt.plot(gamma_range,score)
plt.show()
0.9766081871345029 0.012067926406393264

通过学习曲线,很容就找出了rbf的最佳gamma值。但我们观察到,这其实与线性核函数的准确率一模一样之前的准确率。我们可以多次调整gamma_range来观察结果,可以发现97.6608应该是rbf核函数的极限了。
但对于多项式核函数来说,一切就没有那么容易了,因为三个参数共同作用在一个数学公式上影响它的效果,因此我们往往使用网格搜索来共同调整三个对多项式核函数有影响的参数。依然使用乳腺癌数据集。
from sklearn.model_selection import StratifiedShuffleSplit#用于支持带交叉验证的网格搜索
from sklearn.model_selection import GridSearchCV#带交叉验证的网格搜索
time0 = time()
gamma_range = np.logspace(-10,1,20)
coef0_range = np.linspace(0,5,10)
param_grid = dict(gamma = gamma_range
,coef0 = coef0_range)
cv = StratifiedShuffleSplit(n_splits=5, test_size=0.3, random_state=420)#将数据分为5份,5份数据中测试集占30%
grid = GridSearchCV(SVC(kernel = "poly",degree=1,cache_size=5000
,param_grid=param_grid
,cv=cv)
grid.fit(X, y)
print("The best parameters are %s with a score of %0.5f" % (grid.best_params_,
grid.best_score_))
print(time()-time0)
The best parameters are {'coef0': 0.0, 'gamma': 0.18329807108324375} with a score of 0.96959
13.360332727432251
可以发现,网格搜索为我们返回了参数coef0=0,gamma=0.18329807108324375,但整体的分数是0.96959,虽然比调参前略有提高,但依然没有超过线性核函数核rbf的结果。可见,如果最初选择核函数的时候,你就发现多项式的结果不如rbf和线性核函数,那就不要挣扎了,试试看调整rbf或者直接使用线性。
2.3 硬间隔与软间隔:重要参数C
2.3.1 SVM在软间隔数据上的推广
到这里,我们已经了解了线性SVC的基本原理,以及SVM如何被推广到非线性情况下,还了解了核函数的选择和应用。但实际上,我们依然没有完全了解sklearn当中的SVM用于二分类的全貌。我们之前在理论推导中使用的数据都有一个特点,那就是他们或是完全线性可分,或者是非线性的数据。在我们对比核函数时,实际上用到了一种不同的数据,那就是不完全线性可分的数据集。比如说如下数据集:
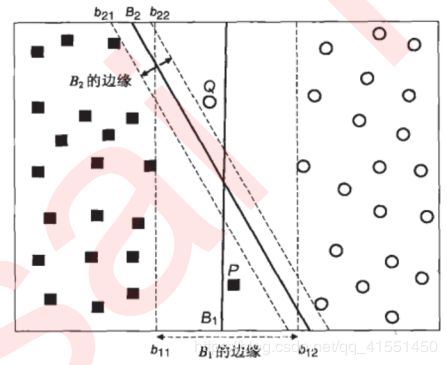
这个数据集和我们最开始介绍SVM如何工作的时候的数据集一模一样,除了多了P和Q两个点。我们注意到,虽然决策边界 B 1 B_1 B1的间隔已经非常宽了,然而点P和Q依然被分错了类别,相反,边际比较小的 B 2 B_2 B2却正确地分出了点P和Q的类别。这里并不是说 B 2 B_2 B2 此时此刻就是一条更好的边界了,与之前的论述中一致,如果我们引入更多的训练数据,或引入测试数据, B 1 B_1 B1 更加宽敞的边界可以帮助它又更好的表现。但是,和之前不一样,现在即便是让边际最大的决策边界 B 1 B_1 B1的训练误差也不可能为0了。此时,我们就需要引入“软间隔”的概念:
| 关键概念:硬间隔与软间隔 |
|---|
| 当两组数据是完全线性可分,我们可以找出一个决策边界使得训练集上的分类误差为0,这两种数据就被称为是存在”硬间隔“的。当两组数据几乎是完全线性可分的,但决策边界在训练集上存在较小的训练误差,这两种数据就被称为是存在”软间隔“。 |
我们可以通过调整我们对决策边界的定义,将硬间隔时得出的数学结论推广到软间隔的情况上,让决策边界能够忍受一小部分训练误差。这个时候,我们的决策边界就不是单纯地寻求最大边际了,因为对于软间隔地数据来说,边际越大被分错的样本也就会越多,因此我们需要找出一个”最大边际“与”被分错的样本数量“之间的平衡。




2.3.2 重要参数C
参数C用于权衡”训练样本的正确分类“与”决策函数的边际最大化“两个不可同时完成的目标,希望找出一个平衡点来让模型的效果最佳。
| 参数 | 含义 |
|---|---|
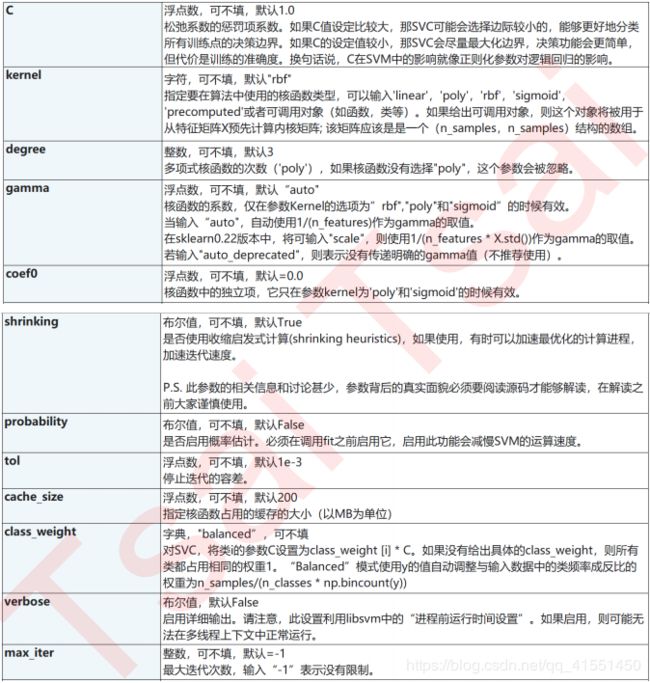
| C | 浮点数,默认1,必须大于等于0,可不填。松弛系数的惩罚项系数。如果C值设定比较大,那SVC可能会选择边际较小的,能够更好地分类所有训练点的决策边界,不过模型的训练时间也会更长。如果C的设定值较小,那SVC会尽量最大化边界,决策功能会更简单,但代价是训练的准确度。换句话说,C在SVM中的影响就像正则化参数对逻辑回归的影响 |
在实际使用中,C和核函数的相关参数(gamma,degree等等)们搭配,往往是SVM调参的重点。与gamma不同,C没有在对偶函数中出现,并且是明确了调参目标的,所以我们可以明确我们究竟是否需要训练集上的高精确度来调整C的方向。默认情况下C为1,通常来说这都是一个合理的参数。 如果我们的数据很嘈杂,那我们往往减小C。当然,我们也可以使用网格搜索或者学习曲线来调整C的值。
#调线性核函数
score = []
C_range = np.linspace(0.01,30,50)
for i in C_range:
clf = SVC(kernel="linear",C=i,cache_size=5000).fit(Xtrain,Ytrain)
score.append(clf.score(Xtest,Ytest))
print(max(score), C_range[score.index(max(score))])
plt.plot(C_range,score)
plt.show()
#换rbf
score = []
C_range = np.linspace(0.01,30,50)
for i in C_range:
clf = SVC(kernel="rbf",C=i,gamma = 0.012742749857031322,cache_size=5000).fit(Xtrain,Ytrain)
score.append(clf.score(Xtest,Ytest))
print(max(score), C_range[score.index(max(score))])
plt.plot(C_range,score)
plt.show()
#进一步细化
score = []
C_range = np.linspace(5,7,50)
for i in C_range:
clf = SVC(kernel="rbf",C=i,gamma =
0.012742749857031322,cache_size=5000).fit(Xtrain,Ytrain)
score.append(clf.score(Xtest,Ytest))
print(max(score), C_range[score.index(max(score))])
plt.plot(C_range,score)
plt.show()
0.9766081871345029 1.2340816326530613
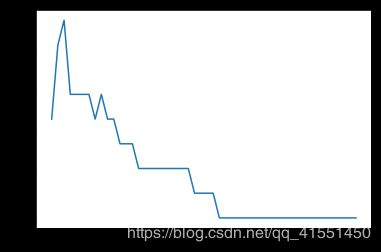
0.9824561403508771 6.130408163265306

0.9824561403508771 5.938775510204081

此时,我们找到了乳腺癌数据集上的最优解:rbf核函数下的98.24%的准确率。当然,我们还可以使用交叉验证来改进我们的模型,获得不同测试集和训练集上的交叉验证结果。但上述过程,为大家展现了如何选择正确的核函数,以及如何调整核函数的参数,过程虽然简单,但是希望可以对大家有所启发。
2.4 总结
本周,我们讲解了支持向量机的原理,向大家介绍了支持向量机的损失函数,拉格朗日函数,拉格朗日对偶函数,预测函数以及这些函数在非线性,软间隔这些情况上的推广。我们介绍了四种核函数,包括它们的特点,适合什么样的数据,有什么相关参数,优缺点,以及什么时候使用。最后我们还讲解了核函数在相关参数上的调参。本节课的内容非常多,但我们对SVM的探索还远远没有结束。下一周我们会继续讲解SVM,包括SVC的模型评价指标,SVC使用中的其他重要参数,重要属性和接口,以及其他重要问题,当然还有案例。希望大家尽力消化这一周的内容,SVC的探索道路依然任重而道远。