Leetcode中的经典算法(归并/分治/快排/数学问题)如何体现在题目中
目录
分治
合并K个排序链表
分治算法递归代码:
14. 最长公共前缀
分治法在排序中的应用:归并排序
148. 排序链表
面试题51. 数组中的逆序对
493. 翻转对
315. 计算右侧小于当前元素的个数
327. 区间和的个数
分治法在排序中的应用:快速排序
215. 数组中的第K个最大元素
各种常用排序总结
数学问题
621. 任务调度器
分治
合并K个排序链表
https://leetcode-cn.com/problems/merge-k-sorted-lists/
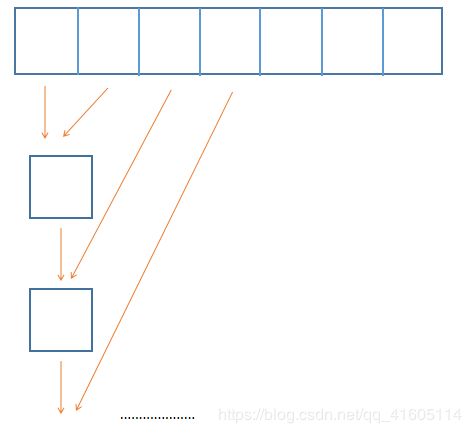
合并两个链表的经验我们有,那么n个也是一样的,我们两个两个合并,如图所示:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* mergeKLists(vector& lists) {
if(lists.empty()) return nullptr;
int size = lists.size();
if(size == 1) return lists[0];
//两个两个合并
int begin = 0;
ListNode* Two = new ListNode();
while(size>1&&beginval<=L2->val)
{
Temp->val = L1->val;
L1 = L1->next;
}
else
{
Temp->val = L2->val;
L2 = L2->next;
}
if(head == nullptr) head = Temp;
if(Pre == nullptr) Pre = Temp;
else {Pre->next = Temp;Pre = Temp;}
}
ListNode* After = L1 == nullptr?L2:L1;
while(After)
{
ListNode* Temp = new ListNode(After->val);
if(head == nullptr) head = Temp;
if(Pre == nullptr) Pre = Temp;
else {Pre->next = Temp;Pre = Temp;}
After = After->next;
}
return head!=nullptr?head:nullptr;
}
}; 显示太浪费了,我们采用典型的分治法的思想:
![]()
图源:https://leetcode-cn.com/problems/merge-k-sorted-lists/solution/he-bing-kge-pai-xu-lian-biao-by-leetcode-solutio-2/
分治算法递归代码:
那么我们程序要怎么写呢?利用递归,非常巧妙
ListNode* merge(vector &lists, int l, int r)
{
if (l == r) return lists[l];
if (l > r) return nullptr;
int mid = l+(r - l)/2;
return List(merge(lists, l, mid), merge(lists, mid + 1, r));
} 当起点终点一样的时候,我们返回原值,起点大于终点,我们返回空,下面我们看看这个递归过程是怎样的
优化时间,分治法完整代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* mergeKLists(vector& lists) {
if(lists.empty()) return nullptr;
int size = lists.size();
if(size == 1) return lists[0];
return merge(lists, 0, size - 1);
}
ListNode* merge(vector &lists, int l, int r)
{
if (l == r) return lists[l];
if (l > r) return nullptr;
int mid = l+(r - l)/2;
return List(merge(lists, l, mid), merge(lists, mid + 1, r));
}
ListNode* List(ListNode* L1,ListNode* L2)
{
if(!L1&&!L2) return nullptr;
ListNode* head = nullptr;
ListNode* Pre = head;
while(L1&&L2)
{
ListNode* Temp = new ListNode( );
if(L1->val<=L2->val)
{
Temp->val = L1->val;
L1 = L1->next;
}
else
{
Temp->val = L2->val;
L2 = L2->next;
}
if(head == nullptr) head = Temp;
if(Pre == nullptr) Pre = Temp;
else {Pre->next = Temp;Pre = Temp;}
}
// cout<val<val);
if(head == nullptr) head = Temp;
if(Pre == nullptr) Pre = Temp;
else {Pre->next = Temp;Pre = Temp;}
After = After->next;
}
return head!=nullptr?head:nullptr;
}
}; 但是每次都要分配空间,实在是不划算,我们原地合并两个链表:
迭代/递归:
class Solution {
public:
ListNode* mergeKLists(vector& lists) {
if(lists.empty()) return nullptr;
int size = lists.size();
if(size == 1) return lists[0];
return merge(lists, 0, size - 1);
}
ListNode* merge(vector &lists, int l, int r)
{
if (l == r) return lists[l];
if (l > r) return nullptr;
int mid = l+(r - l)/2;
return List(merge(lists, l, mid), merge(lists, mid + 1, r));
}
//递归
ListNode* List(ListNode* l1,ListNode* l2)
{
if(!l1) return l2;
else if(!l2) return l1;
else if(l1->valval) {l1->next = List(l1->next,l2);return l1;}
else {l2->next = List(l1,l2->next);return l2;}
}
//迭代
ListNode* List(ListNode* l1,ListNode* l2)
{
if(!l1||!l2) return (l1 == nullptr)?l2:l1;
ListNode NewHead;
ListNode* Pre = &NewHead;
while(l1&&l2)
{
if(l1->valval) {Pre->next = l1;l1 = l1->next;}
else {Pre->next = l2;l2 = l2->next;}
Pre = Pre->next;
}
Pre->next = (l1 == nullptr)?l2:l1;
return NewHead.next;
}
}; 还有更好的办法吗?当然有,使用优先队列:priority_queue
class Solution {
public:
struct Status {
int val;
ListNode *ptr;
bool operator < (const Status &rhs) const {
return val > rhs.val;
}
};
priority_queue q;
ListNode* mergeKLists(vector& lists) {
for (auto node: lists) {
if (node) q.push({node->val, node});
}
ListNode head, *tail = &head;
while (!q.empty()) {
auto f = q.top(); q.pop();
tail->next = f.ptr;
tail = tail->next;
if (f.ptr->next) q.push({f.ptr->next->val, f.ptr->next});
}
return head.next;
}
};
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/merge-k-sorted-lists/solution/he-bing-kge-pai-xu-lian-biao-by-leetcode-solutio-2/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。 算法参考:https://leetcode-cn.com/problems/merge-k-sorted-lists/solution/he-bing-kge-pai-xu-lian-biao-by-leetcode-solutio-2/
14. 最长公共前缀
思想和上面的合并指针一样,都是分支法进行解决,有了上一道题的铺垫,本题要简单的多。
class Solution {
public:
string longestCommonPrefix(vector& strs) {
return cutmid(strs,0,strs.size()-1);
}
string cutmid(vector& strs,int begin,int end)
{
if(begin == end) return strs[begin];
if(begin>end) return "";
int mid = begin + (end - begin)/2;
return Common(cutmid(strs,begin,mid),cutmid(strs,mid+1,end));
}
string Common(string temp1,string temp2)
{
int point = 0;
while(point
分治法在排序中的应用:归并排序
148. 排序链表
https://leetcode-cn.com/problems/sort-list/
本题最难的不是分治,而是你面对的数据结构是链表
我们要从中间切开,那么首选就是快慢指针:
//快慢指针定位:
ListNode* slow = head;
ListNode* fast = head->next;//偶数要定位在第一个
while(fast&&fast->next)
{
slow = slow->next;
fast = fast->next->next;
}
ListNode* Frist = head;
ListNode* Second = slow->next;
slow->next = nullptr;
if(Frist != nullptr&&Second == nullptr) return Frist;切开之后,链表直接断开,分为前后两个部分,再次进行递归
同样我们也有注意,什么时候停止递归,就是当链表只有一个元素的时候,这是second为nullptr,我们需要让frist返回。
本题唯一难点就是这个部分,其他都是非常常规的归并排序和链表的原地合并
完整代码如下:
class Solution {
public:
ListNode* sortList(ListNode* head) {
return mergeSort(head);
}
ListNode* mergeSort(ListNode* head)
{
if(head == nullptr) return nullptr;
//快慢指针定位:
ListNode* slow = head;
ListNode* fast = head->next;//偶数要定位在第一个
while(fast&&fast->next)
{
slow = slow->next;
fast = fast->next->next;
}
ListNode* Frist = head;
ListNode* Second = slow->next;
slow->next = nullptr;
if(Frist != nullptr&&Second == nullptr) return Frist;
ListNode* head1 = mergeSort(Frist);
ListNode* head2 = mergeSort(Second);
//合并部分
ListNode* dummy = nullptr;
ListNode* Pre = dummy;
while(head1&&head2)
{
if(head1->val<=head2->val)
{
if(dummy == nullptr) dummy = head1;
if(Pre == nullptr) Pre = head1;
else { Pre->next = head1; Pre = head1;}
head1 = head1->next;
}
else
{
if(dummy == nullptr) dummy = head2;
if(Pre == nullptr) Pre = head2;
else { Pre->next = head2; Pre = head2;}
head2 = head2->next;
}
}
while(head1) {Pre->next = head1; Pre = head1;head1 = head1->next;}
while(head2) {Pre->next = head2; Pre = head2;head2 = head2->next;}
return dummy;
}
};写法二:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* sortList(ListNode* head) {
// if(head = nullptr)
return mergesort(head);
}
ListNode* mergesort(ListNode* head)
{
if(head == nullptr||head->next == nullptr) return head;
ListNode* slow = head;
ListNode* fast = head->next;
while(fast&&fast->next)
{
slow = slow->next;
fast = fast->next->next;
}
ListNode* Right = slow->next;
slow->next = nullptr;
return Sortlist(mergesort(head),mergesort(Right));
}
ListNode* Sortlist(ListNode* head1,ListNode* head2)//合并链表
{
//返回排序后的头指针
ListNode* dummy = nullptr;
ListNode* pre = nullptr;
while(head1||head2)
{
if(head2&&head1)
{
if(head1->valval)
{
if(dummy == nullptr) dummy = head1;
if(pre == nullptr) pre = head1;
else{pre->next = head1;pre = head1;}
head1 = head1->next;
}
else
{
if(dummy == nullptr) dummy = head2;
if(pre == nullptr) pre = head2;
else{pre->next = head2;pre = head2;}
head2 = head2->next;
}
}
else if(head1)
{
pre->next = head1;pre = head1;head1 = head1->next;
}
else if(head2)
{
pre->next = head2;pre = head2;head2 = head2->next;
}
}
return dummy;
}
};
面试题51. 数组中的逆序对
本题就是归并排序+一行特殊代码:
class Solution {
public:
int reversePairs(vector& nums) {
int size = nums.size();
vectorTemp(size);
return mergeSort(nums,Temp,0,size-1);
}
int mergeSort(vector& nums, vector& Temp, int begin, int end)//返回逆序对的个数
{
if(begin>=end) return 0;//一个字符,只能是0
int mid = begin + (end - begin)/2;
int inv_count = mergeSort(nums,Temp,begin,mid)+mergeSort(nums,Temp,mid+1,end);
int i = begin,j = mid + 1,pos = begin;//分成两段
while(i<=mid&&j<=end)
{
//谁小谁往临时栈中压
if(nums[i] <= nums[j])
{
Temp[pos] = nums[i];
++i;
}
else
{
Temp[pos] = nums[j];
++j;
inv_count += ((mid + 1) - i);//此时左侧数组的个数,本题增加的唯一内容
}
++pos;
}
//还有剩余内容,将剩余内容进行补充
for (int k = i; k <= mid; ++k) {
Temp[pos++] = nums[k];
}
for (int k = j; k <= end; ++k) {
Temp[pos++] = nums[k];
inv_count += ((mid + 1) - i);//此时左侧数组的个数,本题增加的唯一内容
}
//三个begin!!!,细节一定要弄清楚
copy(Temp.begin() + begin, Temp.begin() + end + 1, nums.begin() + begin);
//Temp.begin() + begin, Temp.begin() + end + 1这个区间内,都将代替nums.begin() + begin)
//完成排序的一个过程
return inv_count;
}
}; 代码参考:https://leetcode-cn.com/problems/shu-zu-zhong-de-ni-xu-dui-lcof/solution/shu-zu-zhong-de-ni-xu-dui-by-leetcode-solution/
https://leetcode-cn.com/problems/shu-zu-zhong-de-ni-xu-dui-lcof/solution/bao-li-jie-fa-fen-zhi-si-xiang-shu-zhuang-shu-zu-b/
本题是非常经典的使用归并排序的题目,有几个细节问题需要阐述:
1,临时数组:
int reversePairs(vector& nums) {
int size = nums.size();
vectorTemp(size);
return mergeSort(nums,Temp,0,size-1);
} 我们需要临时数组,同样的,因为递归可能会爆栈,我们需要把临时数组当做参数来传递
如果我们在mergeSort中临时创建Temp,会导致超时,代码无法AC。
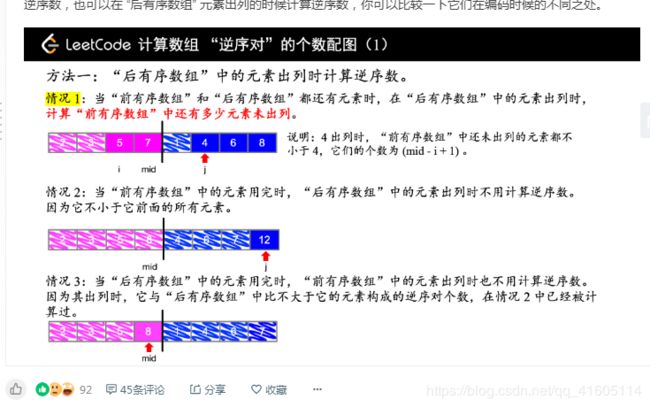
2,统计逆序对的方法:
图源: https://leetcode-cn.com/problems/shu-zu-zhong-de-ni-xu-dui-lcof/solution/bao-li-jie-fa-fen-zhi-si-xiang-shu-zhuang-shu-zu-b/
执行代码如下:
while(i<=mid&&j<=end)//开始归并
{
if(nums[i]<=nums[j])//不构成逆序对
{
Temp[pos] = nums[i++];
//方法二
Res += j-mid+1;
}
else
{
Temp[pos] = nums[j++];
//方法一:
Res += mid - i + 1;
}
pos++;
}3,拷贝过程:
方式一:
//拷贝过程
copy(Temp.begin() + begin,Temp.begin() + end + 1,nums.begin() + begin);方式二:
for(int k = begin;k<=end;++k) nums[k] = Temp[k];4,传递参数:
左右都是闭
return megresort(nums,Temp,0,nums.size()-1);//左右区间是全闭
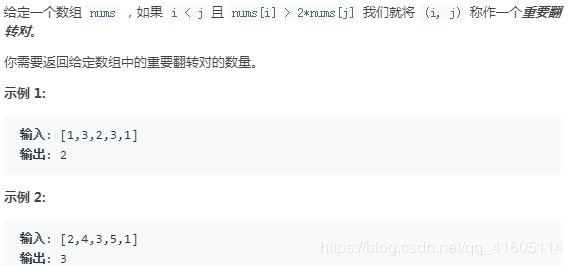
493. 翻转对
https://leetcode-cn.com/problems/reverse-pairs/
上一题的升级版本
我们在排序前,对左右两个数组进行遍历,查找翻转对,之后再进行归并排序
这次我们在归并的过程中进行查询,而不是在归并的同时进行查询
class Solution {
public:
int reversePairs(vector& nums) {
int size = nums.size();
vectorTemp(size);
return mergoSort(nums,Temp,0,size-1);
}
int mergoSort(vector& nums,vector& Temp,int begin,int end)
{
if(begin>=end) return 0;//一个字符,只能是0
int mid = begin + (end - begin)/2;
int Res = mergoSort(nums,Temp,begin,mid)+mergoSort(nums,Temp,mid+1,end);
int i = begin,j = mid + 1,pos = begin;//分成两段
//遍历两端数组,对比看谁是二倍关系
while(i<=mid&&j<=end)//比完就完了
{
if((long)nums[i] > 2*(long)nums[j])//找到
{Res += mid + 1 - i;j++;}
else i++;
}
//归并排序
i = begin,j = mid + 1;
while(i<=mid&&j<=end)
{
//谁小谁往临时栈中压
if(nums[i] <= nums[j])
{Temp[pos] = nums[i++];}
else
{Temp[pos] = nums[j++];}
++pos;
}
//肯定有没有入Temp的部分
for (int k = i; k <= mid; ++k) {Temp[pos] = nums[k];pos++;}
for (int k = j; k <= end; ++k) {Temp[pos] = nums[k];pos++;}
copy(Temp.begin() + begin, Temp.begin() + end + 1, nums.begin() + begin);
return Res;
}
};
315. 计算右侧小于当前元素的个数
https://leetcode-cn.com/problems/count-of-smaller-numbers-after-self/
索引数组,本题最难的地方,就是索引数组
因为可能出现重复内容,不能使用Hash表,使用pair对元素和索引进行一一对应的记录
其他部分不变,我们依旧循环,只是现在将元素和索引绑定在一起了
初始化:
vector> index;//关联每个数和它的序号
for(int i = 0;i 之后我们访问index中的内容,first就是数组元素,second就是数组索引
我们来看看核心代码:
vector> Temp;
while(i<=mid&&j<=end)
{
if(index[i].first<=index[j].first)//后面的大,顺序不影响
{
Number[index[i].second] += j - mid - 1;//当前序出列时,查看后列已经出列了多少个
Temp.push_back(index[i++]);
}
else//前面的比后面的大
{
Temp.push_back(index[j++]);
}
} 完整代码:
class Solution {
public:
vector> index;//关联每个数和它的序号
vector countSmaller(vector& nums) {
int size = nums.size();
vectorNumber(size,0);//保存结果
vector> index;//关联每个数和它的序号
for(int i = 0;i>& index,vector& Number,int begin,int end)
{
if(begin>=end) return;
int mid = begin + (end - begin)/2;
mergeSort(index,Number,begin,mid);
mergeSort(index,Number,mid+1,end);
int i = begin,j = mid+1;
//换个思路,在前序数组出列的时候,计算后续数组有几个出列了,那么出列的个数就是以该数字为开头的逆序对
vector> Temp;
while(i<=mid&&j<=end)
{
if(index[i].first<=index[j].first)//后面的大,顺序不影响
{
Number[index[i].second] += j - mid - 1;//当前序出列时,查看后列已经出列了多少个
Temp.push_back(index[i++]);
}
else//前面的比后面的大
{
Temp.push_back(index[j++]);
}
}
for(int k = i;k<=mid;++k)
{
Temp.push_back(index[k]);
Number[index[k].second] += j - mid - 1;
}
for(int k = j;k<=end;++k) Temp.push_back(index[k]);
for (int m = 0, n = begin; m < Temp.size(); m++, n++){
index[n] = Temp[m];
}
return;
}
};
327. 区间和的个数
https://leetcode-cn.com/problems/count-of-range-sum/
参考算法:https://leetcode-cn.com/problems/count-of-range-sum/solution/327qu-jian-he-de-ge-shu-ti-jie-zong-he-by-xu-yuan-
分治法在排序中的应用:快速排序
215. 数组中的第K个最大元素
https://leetcode-cn.com/problems/kth-largest-element-in-an-array/
快速排序,快排是典型的分治法和双指针的巧妙结合,原理此处不再过多的赘述,快排不稳定,和递归时间复杂度和递归树的高度直接相关,有时候枢纽选择不了中间值,就会很慢,下面是快排的普通版本
class Solution {
public:
int findKthLargest(vector& nums, int k) {
int size = nums.size()-1;
quickSelect(nums,0,size);//快速排序
// for(auto item:nums) cout<& a, int l, int r)
{
if(l>=r) return;
int pivot = Partition(a,l,r);
quickSelect(a,l,pivot-1);
quickSelect(a,pivot+1,r);
}
int Partition(vector& a, int l, int r)
{
int temp = a[l];
while(l=temp) r--;
swap(a[r],a[l]);
while(l 我们尝试对快速排序进行优化:
1:对枢纽进行优化
class Solution {
public:
int findKthLargest(vector& nums, int k) {
int size = nums.size()-1;
quickSelect(nums,0,size);//快速排序
// for(auto item:nums) cout<& a, int left, int right)
{
if(left>=right) return;
int pivot = Partition(a,left,right);
quickSelect(a,left,pivot-1);
quickSelect(a,pivot+1,right);
}
int Partition(vector& a, int left, int right)
{
ChangePivot(a,left,right);//枢纽优化
int temp = a[left];
while(left=temp) right--;
swap(a[right],a[left]);
while(left& a, int left, int right)//让枢纽尽可能是中间值
{
int mid = left + (right - left)/2;
if(a[left]>a[right]) swap(a[left],a[right]);//保证左端最小
if(a[mid]>a[right]) swap(a[mid],a[right]);//保证中间较小
if(a[mid]>a[left]) swap(a[mid],a[left]);//保证左端较小
}
}; 2:优化不必要的交换
class Solution {
public:
int findKthLargest(vector& nums, int k) {
int size = nums.size()-1;
quickSelect(nums,0,size);//快速排序
// for(auto item:nums) cout<& a, int left, int right)
{
if(left>=right) return;
int pivot = Partition(a,left,right);
quickSelect(a,left,pivot-1);
quickSelect(a,pivot+1,right);
}
int Partition(vector& a, int left, int right)
{
// ChangePivot(a,left,right);//枢纽优化
int temp = a[left];
while(left=temp) right--;
a[left] = a[right];
while(left& a, int left, int right)
// {
// int mid = left + (right - left)/2;
// if(a[left]>a[right]) swap(a[left],a[right]);//保证左端最小
// if(a[mid]>a[right]) swap(a[mid],a[right]);//保证中间较小
// if(a[mid]>a[left]) swap(a[mid],a[left]);//保证左端较小
// }
}; 3:优化递归排序
class Solution {
public:
int findKthLargest(vector& nums, int k) {
int size = nums.size()-1;
quickSelect(nums,0,size);//快速排序
// for(auto item:nums) cout<& a, int left, int right)
{
if(left>=right) return;
while(left& a, int left, int right)
{
// ChangePivot(a,left,right);//枢纽优化
int temp = a[left];//此处必须是第一个元素,快排的核心其实还是为找temp在数组总的位置
//而且,后面中间分隔的做法,也是排除了temp这个元素的,务必注意细节
while(left=temp) right--;
a[left] = a[right];
while(left& a, int left, int right)
// {
// int mid = left + (right - left)/2;
// if(a[left]>a[right]) swap(a[left],a[right]);//保证左端最小
// if(a[mid]>a[right]) swap(a[mid],a[right]);//保证中间较小
// if(a[mid]>a[left]) swap(a[mid],a[left]);//保证左端较小
// }
}; 4,小数组使用插入排序
class Solution {
public:
int findKthLargest(vector& nums, int k) {
if(nums.empty()) return -1;
QuickSort(nums,0,nums.size()-1);
// for(auto item:nums) cout<& nums, int begin,int end){
if(begin>=end) return;
if(end-begin>7){
while(begin& nums, int begin,int end){
int temp = nums[begin];
while(begin=temp) end--;
nums[begin] = nums[end];
while(begin& nums){//插入排序
for(int i = 1;i=0;--j){
if(nums[j]>nums[j+1]) swap(nums[j+1],nums[j]);
}
}
}
}
};
各种常用排序总结
378. 有序矩阵中第K小的元素 https://leetcode-cn.com/problems/kth-smallest-element-in-a-sorted-matrix/
(冒泡,选择,插入,快排,归并)
class Solution {
public:
int kthSmallest(vector>& matrix, int k) {
//经典排序轮着来用
vectorTarget;
int n = matrix.size();
for(int i = 0;i & Num){
int size = Num.size();
bool flag = true;//优化
for(int i = 0;i=i;--j)
{
if(Num[j]>Num[j+1]) {swap(Num[j],Num[j+1]);flag = true;}
}
}
}
//简单选择排序(超时):固定i,在i到size之间找最小值,放在i的位置上
void SelectSort(vector & Num){
int size = Num.size();
int Index = 0;
for(int i = 0;iNum[j]) Index = j;
}
if(i!=Index) swap(Num[i],Num[Index]);
}
}
//插入排序
// 找数组中有序部分,然后不断更新,如果i的位置是无序内容,那么我们把无序内容放置到有序内容中
void InsertSort(vector & Num){
int size = Num.size();
for(int i = 1;i=0;--j)
{
if(temp & Num,int begin,int end){
if(begin>=end) return;
int mid = begin + (end - begin)/2;
mergeSort(Num,begin,mid);
mergeSort(Num,mid+1,end);
vector Temp(Num.size(),0);
int i = begin,pos = begin,j = mid+1;
while(i<=mid&&j<=end)
{
if(Num[i]>Num[j]) Temp[pos++] = Num[j++];
else Temp[pos++] = Num[i++];
}
for(int k = i;k<=mid;++k) Temp[pos++] = Num[k];
for(int k = j;k<=end;++k) Temp[pos++] = Num[k];
for(int k = begin;k<=end;++k) Num[k] = Temp[k];
}
//快排
void quickSort(vector & Num,int begin,int end){
if(begin>=end) return;
int piv = Partition(Num,begin,end);
quickSort(Num,begin,piv-1);
quickSort(Num,piv+1,end);
}
int Partition(vector & Num,int begin,int end){
int temp = Num[begin];//选第一个点
while(begin=temp) end--;
Num[begin] = Num[end];
while(begin
数学问题
621. 任务调度器
https://leetcode-cn.com/problems/task-scheduler/
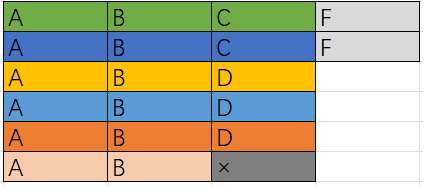
本题最合理的想法,就是执行不同的n+1个任务,如此循环,就能达到最短时间,但是有时候我们的不同任务的个数有限,必须要有待命的部分来填充:
下面的图源来自:https://leetcode-cn.com/problems/task-scheduler/solution/tong-zi-by-popopop/
我们先找到出现次数最多的一个任务,将其作为我们的高,显然n+1作为长是最合理的
我们在最后一行的时候,会出现以上情况,此时只剩下A任务,我们执行即可,我们记A出现的个数是MaxNumber
那么此时的时间是:(MaxNumber-1)*(n+1)+1:
那么我们现在加入其它任务进来:
此时的时间是:(MaxNumber-1)*(n+1)+2,我们可以看到,前面部分没有任何影响,只是最后执行的时候需要计算预留任务
那么当任务很多时,怎么办?
我们将多余的任务一次性在其他位置执行完,那么我们会发现,当任务足够多的时候,没有所谓的待命时间,执行时间就是所有任务的个数
我们计算(MaxNumber-1)*(n+1)+ 预留任务,最后和所有任务出现次数做比较,谁大选择谁
本题实质就是一道数学问题。
class Solution {
public:
int leastInterval(vector& tasks, int n) {
if(tasks.empty()) return 0;
//统计任务种类
unordered_mapM;
int MaxNumber = 0;//求出现最多次的任务个数
for(auto item : tasks)
{
M[item]++;
MaxNumber = max(MaxNumber,M[item]);
}
int ans = (MaxNumber - 1)*(n + 1);//n+1是最合理的间隔,count-1是完整执行任务的区间
//计算预留任务的个数,起码一个,至多就不一定了
for (auto item : M) if (item.second == MaxNumber) ans++;
return max((int)tasks.size(), ans); //最后在两者中取最大的值
}
};
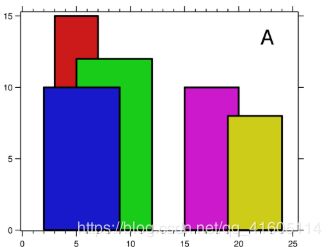
// 代码参考:https://leetcode-cn.com/problems/task-scheduler/comments/201823 218. 天际线问题
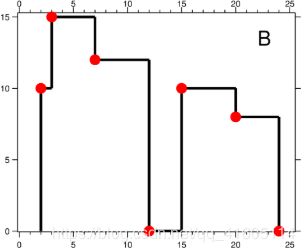
https://leetcode-cn.com/problems/the-skyline-problem/
如何打乱一个数组:
384. 打乱数组
https://leetcode-cn.com/problems/shuffle-an-array/
https://leetcode-cn.com/problems/shuffle-an-array/solution/xi-pai-suan-fa-shen-du-xiang-jie-by-labuladong/