分箱、离散化、线性模型和树

数据表示的最佳方法不仅取决于数据的语义，还取决于所使用的模型的种类。线性模型与基于树的模型（比如决策树、梯度提升树和随机森林）是两种成员很多同时又非常常用的模型，它们在处理不同的特征表示时就具有非常不同的性质。本节以wave数据集为例，它只有一个输入特征。

1.线性回归模型和决策树回归在数据集上的对比

from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor

X, y = mglearn.datasets.make_wave(n_samples=100)
line = np.linspace(-3, 3, 1000, endpoint=False).reshape(-1, 1)

reg = DecisionTreeRegressor(min_samples_split=3).fit(X, y)
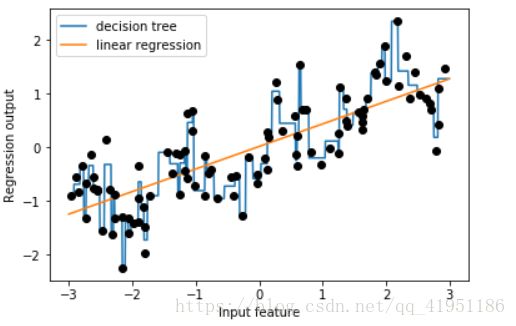
plt.plot(line, reg.predict(line), label="decision tree")

reg = LinearRegression().fit(X, y)
plt.plot(line, reg.predict(line), label="linear regression")

plt.plot(X[:, 0], y, 'o', c='k')
plt.ylabel("Regression output")
plt.xlabel("Input feature")
plt.legend(loc="best")

                                       

线性模型只能对线性关系建模，对于单个特征情况就是直线。决策树可以构建更为复杂的数据模型，但这强烈依赖于数据表示。分箱（也叫做离散化）可以让线性模型在连续数据上变得更加强大。

2.分箱操作处理输入数据

分箱：确定输入特征的范围，然后将区间等距划分成一定数目的小区间，即箱子，将每个特征的值变成其所在箱子的编号值。

（1）确定箱子

bins = np.linspace(-3, 3, 11)
print("bins: {}".format(bins))

（2）记录每个特征所属的箱子

which_bin = np.digitize(X, bins=bins)
print("\nData points:\n", X[:5])
print("\nBin membership for data points:\n", which_bin[:5])

 

（3）训练模型

分箱模型将数据集中的单个连续输入特征变换为一个分类特征，用于表示数据点所在的箱子。要想在这个数据上使用scikit-learn模型，我们利用preprocessing模块的OneHotEncoder将离散特征转换成one-hot编码。

from sklearn.preprocessing import OneHotEncoder
# transform using the OneHotEncoder
encoder = OneHotEncoder(sparse=False)
# encoder.fit finds the unique values that appear in which_bin
encoder.fit(which_bin)
# transform creates the one-hot encoding
X_binned = encoder.transform(which_bin)
print(X_binned[:5])

 

利用one-hot编码后的数据构建新的线性模型和新的决策树模型。

line_binned = encoder.transform(np.digitize(line, bins=bins))

reg = LinearRegression().fit(X_binned, y)
plt.plot(line, reg.predict(line_binned), label='linear regression binned')

reg = DecisionTreeRegressor(min_samples_split=3).fit(X_binned, y)
plt.plot(line, reg.predict(line_binned), label='decision tree binned')
plt.plot(X[:, 0], y, 'o', c='k')
plt.vlines(bins, -3, 3, linewidth=1, alpha=.2)
plt.legend(loc="best")
plt.ylabel("Regression output")
plt.xlabel("Input feature")

 

虚线和实线完全重合，说明线性回归模型和决策树做出了完全相同的预测。对于每个箱子，二者都预测一个常数值。分箱特征对基于树的模型通常不会产生更好的结果，因为树模型可以学习在任何位置划分数据。从某种意义上来看，决策树可以学习如何分箱对预测这些数据最为有用。此外，决策树可以同时查看多个特征，而分箱通常只针对单个特征。不过，线性模型的表现力在数据变换后得到极大的提高。

对于特定的数据集，如果有充分的理由使用线性模型（比如数据集很大、维度很高），但有些特征与输出的关系是非线性的，则 分箱是提高建模能力的好方法。

4.分箱特征的扩展

线性模型对wave数据集中的每个箱子都学到一个常数值，我们知道，线性模型不仅可以学习偏移，还可以学习斜率。想要向分箱数据的线性模型上添加斜率，一种方法是重新加入原始特征（图中的x轴），这样会得到11维的数据集。

X_combined = np.hstack([X, X_binned])
print(X_combined.shape)

reg = LinearRegression().fit(X_combined, y)

line_combined = np.hstack([line, line_binned])
plt.plot(line, reg.predict(line_combined), label='linear regression combined')

for bin in bins:
    plt.plot([bin, bin], [-3, 3], ':', c='k', linewidth=1)
plt.legend(loc="best")
plt.ylabel("Regression output")
plt.xlabel("Input feature")
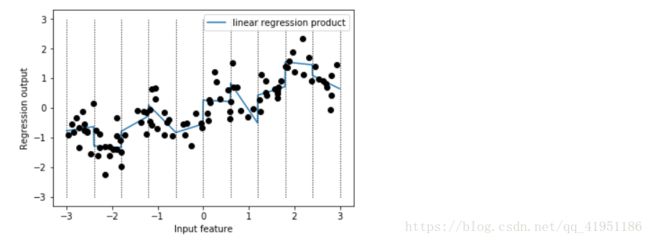
plt.plot(X[:, 0], y, 'o', c='k')

 

上个例子中，学到的斜率都相同，似乎不是很有用，我们希望每个箱子都学到一个不同的斜率。为了实现这一点，我们可以添加交互项特征，用来表示数据点所在的箱子以及数据点在x轴上的位置。这个特征是箱子指示符与原始特征的乘积。

X_product = np.hstack([X_binned, X * X_binned])
print(X_product.shape)

reg = LinearRegression().fit(X_product, y)

line_product = np.hstack([line_binned, line * line_binned])
plt.plot(line, reg.predict(line_product), label='linear regression product')

for bin in bins:
    plt.plot([bin, bin], [-3, 3], ':', c='k', linewidth=1)

plt.plot(X[:, 0], y, 'o', c='k')
plt.ylabel("Regression output")
plt.xlabel("Input feature")
plt.legend(loc="best")