2019年第十届蓝桥杯C/C++ B组省赛题

试题A——组队

思路：这个题其实很简单，只需要口算就行了，不需要写程序，需要注意的是一个球员如果两个最高分的话，只能取一个。
很多种取法，比如：97+99+99+97+98
答案：490

试题B——年号字串

思路：这相当于一道26进制的题目，但又不完全是；
答案：BYQ

代码：

#include
using namespace std;
int main()
{
  int n=2019;
  string t="";
  while(n){
  	int k=n%26;
  	t+=('A'+k-1);
  	n/=26;
  }
  reverse(t.begin(),t.begin()+t.size());
  cout<<t<<endl;
  return 0;
}

reverse对容器中的元素进行反转，string用法如下：
string s;
reverse(s.begin(),s.begin()+3);//对于字符串s[0]到s[2]进行反转

试题C——数列求值

给定数列1,1,1,3,5,9,17,…，从第4项开始，每项都是前3项的和。求
第20190324项的最后4位数字。
【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一
个4位整数（提示：答案的千位不为0），在提交答案时只填写这个整数，填写
多余的内容将无法得分。

思路：类似于斐波拉奇数列，就是这个只需要关注后四位数字，那么对于每个数%10000就可以了

答案： 4659

代码：

#include
using namespace std;
int a[30000000];
int main()
{
  a[1]=a[2]=a[3]=1;
  for(int i=4;i<=20190324;i++){
  	a[i]=(a[i-3]+a[i-2]+a[i-1])%10000;
  }
  cout<<a[20190324];
  return 0;
}

试题D——数的分解

思路：写一个判定一个数是否包含数字2和4的函数，主函数里可以二重循环，直接枚举就可以了

答案：40785

代码：

#include
using namespace std;
int iss(int x){
	while(x){
		int k=x%10;
		if(k==2||k==4) return 0;
		x/=10;
	}
	return 1;
}
int main()
{
  int n=2019,x=0;
  for(int i=1;i<2013;i++){
  	for(int j=i+1;j<2018&&iss(i);j++){
  	        int k=n-i-j;
  	        if(j>=k) continue;
  			if(iss(i)&&iss(j)&&iss(k)) x++;
	  }
  }
  cout<<x<<endl;
  return 0;
}

试题E——迷宫




思路：求最短路径，这一题用广度优先搜索去写就可以了。
答案：DDDDRRURRRRRRDRRRRDDDLDDRDDDDDDDDDDDDRDDRRRURRUURRDDDDRDRRRRRRDRRURRDDDRRRRUURUUUUUUULULLUUUURRRRUULLLUUUULLUUULUURRURRURURRRDDRRRRRDDRRDDLLLDDRRDDRDDLDDDLLDDLLLDLDDDLDDRRRRRRRRRDDDDDDRR
代码：

#include
using namespace std;
char r[]="DLRU";
char a[100][100];
bool f[100][100];
int x[]={1,0,0,-1};
int y[]={0,-1,1,0};
int n=30,m=50;
struct s{
	int xx,yy,step;
	string str;
	s(int x,int y,int ss,string sp){
		xx=x,yy=y,step=ss,str=sp;
	}
};
void bfs(int c,int d){
	queue<s>p;
	p.push(s(c,d,0,""));
	f[c][d]=true;
	while(!p.empty()){
		s t=p.front();
		if(t.xx==n-1&&t.yy==m-1){//到达了终点
		   cout<<t.str<<endl;
		   return ; 
		}
		p.pop();
		for(int i=0;i<4;i++){
			int dx=t.xx+x[i],dy=t.yy+y[i];
			if(dx>=0&&dx<n&&dy>=0&&dy<m&&!f[dx][dy]&&a[dx][dy]=='0'){
				p.push(s(dx,dy,t.step+1,t.str+r[i]));
				f[dx][dy]=1;
			}
		}
	}
}
int main()
{
	for(int i=0;i<n;i++){
		for(int j=0;j<m;j++){
			cin>>a[i][j];
		}
	}
	bfs(0,0);
    return 0;
}

试题F——特别数的和


水题
代码：

#include
using namespace std;
int n;
long long ans=0;
int main()
{
   cin>>n;
   for(int i=1;i<=n;i++){
   	int t=i,flag=0;
   	while(t){
   		int k=t%10;
   		if(k==0||k==1||k==2||k==9){
   			flag=1;
			break;
		   }
   		t/=10;
	   }
	   if(flag) ans+=i;
   }
   cout<<ans<<endl;
   return 0;
}

试题G——完全二叉树的权值


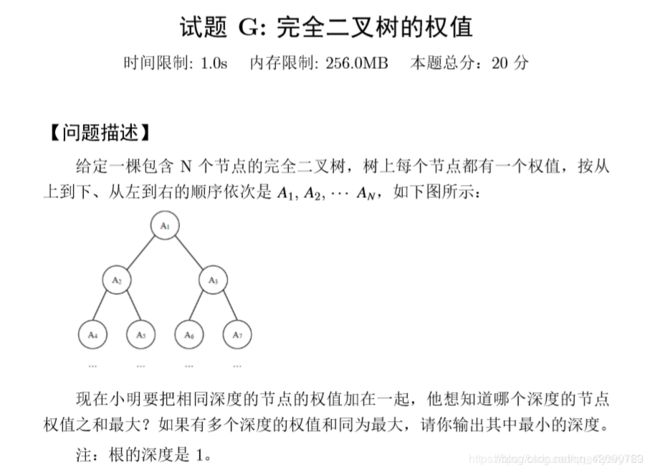
思路：并不需要建树，计算每一层的权值，然后进行比较就可以了，需要注意，题目没说是满二叉树，所以需要注意，并且权值最大有可能是负数，所以默认最大值不能初始化为0，那会导致错误

代码：

#include
using namespace std;
int a[101000];
int p(int x){
	int t=1;
	while(x--)  t*=2;
	 return t;
}
int main()
{
	int n,t=1,i=2,j=2;
	scanf("%d %d",&n,&a[1]);
	long long maxx=a[1];
	for(int i=2;i<=n;i++) scanf("%d",&a[i]);
	while(i<=n){
		long long k=0;
	  for(;i<p(j)&&i<=n;i++)  k+=a[i];
	if(k>maxx)   maxx=k,t=j;
	j++;
	//cout<
}
   cout<<t<<endl;
   return 0;
}

试题H——等差数列

思路：需要用到gcd求最大公约数。要想知道最多有多少项，知道公差d就可以了，最后的答案为 (a[n-1]-a[0])/d+1,但是只通过90%，后来在网上搜了别人的博客才想起来有一个坑点，如果给的数全都相同，那么应该输出的是长度n
代码：

#include
using namespace std;
int n,a[100100];
int gcd(int a,int b){
	return b==0?a:gcd(b,a%b);
}
int main()
{
    scanf("%d",&n);
    for(int i=0;i<n;i++)  scanf("%d",&a[i]);
    sort(a,a+n);
    int x=a[1]-a[0];
    for(int i=2;i<n;i++){
    	x=gcd(x,a[i]-a[i-1]);
	}
	if(x==0) cout<<n<<endl;
	else 
    cout<<(a[n-1]-a[0])/x+1<<endl;
    return 0;
}

试题I——后缀表达式

只通过了部分例子，不知道应该怎么思考了，会的大神可以告诉我下思路，感谢~~

代码：

#include
using namespace std;
long long  x=0;
int a[210000];
int main()
{
	int n,m,t=0;
	cin>>n>>m;
	for(int i=0;i<n+m+1;i++){
		cin>>a[i];
		x+=a[i];
	}
	sort(a,a+n+m+1);
	if(a[0]>=0) x=x;
	else {
		while(a[t]<0&&m--){
			x-=2*a[t],t++;
		}
	}
   cout<<x<<endl;
    return 0;
}

试题J——灵能传输

输入：

输出：

样例输入：

3
3
5 -2 3
4
0 0 0 0
3
1 2 3

样例输出：

3
0
3

提示
对于第一组询问：
对2 号高阶圣堂武士进行传输操作后a1 = 3，a2 = 2，a3 = 1。答案为3。
对于第二组询问：
这一组高阶圣堂武士拥有的灵能都正好可以让他们达到最佳战斗状态。