hmm隐马尔可夫真的那么难吗?
hmm隐马尔可夫真的那么难吗?
首先上代码
这里是github上的关于hmm的:
- 概率计算问题:前向-后向算法
- 学习问题:Baum-Welch算法(状态未知)
- 预测问题:Viterbi算法
https://github.com/TimVerion/HMM_code
需要的理论基础(可以跳过)
信息熵
首先了解一下过去化学学习的熵,热力学中表征物质状态的参量之一,用符号S表示,其物理意义是体系混乱程度的度量。克劳修斯于 1865 年的论文中定义了“熵” ,其中有两句名言:“宇宙的能量是恒定的。”,“宇宙的熵趋于最大值。”
信息量:指的是一个样本/事件所蕴含的信息,如果一个事件的概率越大,那么就
可以认为该事件所蕴含的信息越少。极端情况下,比如:“太阳从东方升起”,
因为是确定事件,所以不携带任何信息量。
信息熵:1948年,香农引入信息熵;一个系统越是有序,信息熵就越低,一个系统越是混乱,信息熵就越高,所以信息熵被认为是一个系统有序程度的度量。信息熵就是用来描述系统信息量的不确定度。
信息熵(Entropy)公式:
− ∑ i = 1 n p i l o g 2 ( p i ) -\sum_{i=1}^np_ilog_2(p_i) −i=1∑npilog2(pi)

High Entropy(高信息熵):表示随机变量X是均匀分布的,各种取值情况是等概
率出现的。Low Entropy(低信息熵):表示随机变量X各种取值不是等概率出现。可能出现
有的事件概率很大,有的事件概率很小。
例子:
最大熵模型
机器学习中经常提到的最大熵的思想,就是当你要猜一个概率分布时,如果你对这个分布一无所知,那就猜熵最大的均匀分布,如果你对这个分布知道一些情况,那么,就猜满足这些情况的熵最大的分布,就像我们使用最大似然去预测一样。
例子:软银的孙正义他强调商战要达到“不战而屈人之兵”,避免“不打败仗”,就得从事优势职业。
孙正义投资雅虎,阿里,网约车火了便投资中国的滴滴和美国的Uber,也就是不把所有鸡蛋放进一个篮子里,这正是最大熵原理。
与最大熵思想区分开来后,我们要知道最大熵模型就是让信息熵最大,而所谓的条件最大熵模型,就是在一定约束下条件熵最大的模型。再直白一点就是我们要保留全部的不确定性,将风险降到最小。
也就是当从模型总体随机抽取n组样本观测值后,最合理的参数估计量应该使得从模型中抽取该n组样
本观测值的概率最大,这样我们便构造了一个最大熵模型,没错这正是最大似然估计的定义。
最大熵模型,可以说是集简与繁于一体,形式简单,实现复杂。值得一提的是,在Google的很多产品中,比如机器翻译,都直接或间接地用到了最大熵模型。
贝叶斯算法
三门问题:出自美国的电视游戏节目。参赛者会看见三扇关闭了的门,其中一扇的后面有一辆汽车,选中后面有车的那扇门可赢得该汽车,另外两扇门后面则各藏有一只山羊。当参赛者选定了一扇门,但未去开启它的时候,节目主持人开启剩下两扇门的其中一扇,露出其中一只山羊。主持人其后会问参赛者要不要换另一扇仍然关上的门。问题是:换另一扇门会否增加参赛者赢得汽车的机率?如果严格按照上述的条件,即主持人清楚地知道,自己打开的那扇门后是羊,那么答案是会。不换门的话,赢得汽车的几率是1/3。换门的话,赢得汽车的几率是2/3。
先验概率P(A):在不考虑任何情况下,A事件发生的概率
条件概率P(B|A):A事件发生的情况下,B事件发生的概率
后验概率P(A|B):在B事件发生之后,对A事件发生的概率的重新评估
P ( A ∣ B ) = P ( A B ) / P ( B ) P(A|B) = P(AB)/P(B) P(A∣B)=P(AB)/P(B)
全概率:如果A和A’构成样本空间的一个划分,那么事件B的概率为:A和A’的概
率分别乘以B对这两个事件的概率之和。
P ( B ) = ∑ i = 1 n P ( A i ) ∗ P ( B ∣ A i ) P(B) =\sum_{i=1}^nP(A_i)*P(B|A_i) P(B)=i=1∑nP(Ai)∗P(B∣Ai)
有上面的知识推出贝叶斯公式(后验概率):
P ( A ∣ B ) = P ( A ) ∗ P ( B ∣ A ) P ( B ) = P ( A ) ∗ P ( B ∣ A ) ∑ i = 1 n P ( B ∣ A i ∗ P ( A i ) ) P(A|B)=\frac{P(A)*P(B|A)}{P(B)} = \frac{P(A)*P(B|A)}{\sum_{i=1}^nP(B|A_i*P(A_i))} P(A∣B)=P(B)P(A)∗P(B∣A)=∑i=1nP(B∣Ai∗P(Ai))P(A)∗P(B∣A)
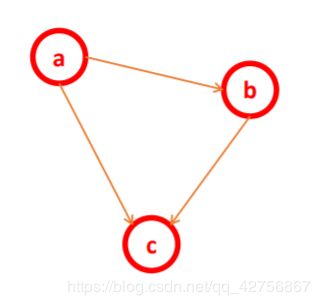
贝叶斯网络
把某个研究系统中涉及到的随机变量,根据是否条件独立绘制在一个有向图中,
就形成了贝叶斯网络。
贝叶斯网络(Bayesian Network),又称有向无环图模型(directed acyclic
graphical model, DAG),是一种概率图模型,根据概率图的拓扑结构,考察一
组随机变量{X1,X2,…,Xn}及其N组条件概率分布(Conditional Probabililty
Distributions, CPD)的性质
当多个特征属性之间存在着某种相关关系的时候,使用朴素贝叶斯算法就没法解
决这类问题,那么贝叶斯网络就是解决这类应用场景的一个非常好的算法。
一般而言,贝叶斯网络的有向无环图中的节点表示随机变量,可以是可观察到的
变量,或隐变量,未知参数等等。连接两个节点之间的箭头代表两个随机变量之
间的因果关系(也就是这两个随机变量之间非条件独立),如果两个节点间以一个
单箭头连接在一起,表示其中一个节点是“因”,另外一个是“果”,从而两节
点之间就会产生一个条件概率值。注意:每个节点在给定其直接前驱的时候,条件独立于其后继。
贝叶斯网络的关键方法是图模型,构建一个图模型我们需要把具有因果联系的各
个变量用箭头连在一起。贝叶斯网络的有向无环图中的节点表示随机变量。连接
两个节点的箭头代表此两个随机变量是具有因果关系的。
贝叶斯网络是模拟人的认知思维推理模式的,用一组条件概率以及有向无环图对
不确定性因果推理关系建模
P(a,b, c) = P(c | a,b)*P(b | a)*P(a)
EM算法
上面的知识点讲到了MLE(最大似然估计),这里先说一下MAP(最大后验概率),MAP和MLE一样,都是通过样本估计参数θ的值;在MLE中,是使似然函数P(x|θ)最大的时候参数θ的值,MLE中假设先验概率是一个等值的;而在MAP中,则是求θ使P(x|θ)P(θ)的值最大,这也就是要求θ值不仅仅是让似然函数最大,同时要求θ本身出现的先验概率也得比较大。
可以认为MAP是贝叶斯算法的一种应用:
P ( θ ∣ X ) = P ( θ ) ∗ P ( X ∣ θ ) P ( X ) → a r g max θ P ( θ ∣ X ) → a r g max θ P ( θ ) P ( X ∣ θ ) P(θ|X)=\frac{P(θ)*P(X|θ)}{P(X)}\to arg \max_{θ}P(θ|X) \to arg\max_{θ}P(θ)P(X|θ) P(θ∣X)=P(X)P(θ)∗P(X∣θ)→argθmaxP(θ∣X)→argθmaxP(θ)P(X∣θ)
EM算法(Expectation Maximization Algorithm, 最大期望算法)是一种迭代类型
的算法,是一种在概率模型中寻找参数最大似然估计或者最大后验估计的算法,
其中概率模型依赖于无法观测的隐藏变量。
EM算法流程:
-
初始化分布参数
-
重复下列两个操作直到收敛:
E步骤:估计隐藏变量的概率分布期望函数;
M步骤:根据期望函数重新估计分布参数
EM实现的过程中还会有一个Jensen不等式知识点,它使得我们可以假设隐含数据并形成极大化模型,然后对联合概率求最大值直到收敛。
"""
实现GMM高斯混合聚类
根据EM算法流程实现这个流程
"""
import numpy as np
from scipy.stats import multivariate_normal
def train(x, max_iter=100):
"""
进行GMM模型训练,并返回对应的μ和σ的值(假定x数据中的簇类别数目为2)
:param x: 输入的特征矩阵x
:param max_iter: 最大的迭代次数
:return: 返回一个五元组(pi, μ1, μ2,σ1,σ2)
"""
# 1. 获取样本的数量m以及特征维度n
m, n = np.shape(x)
# 2. 初始化相关变量
# 以每一列中的最小值作为mu1,mu1中的元素数目就是列的数目(n)个
mu1 = x.min(axis=0)
mu2 = x.max(axis=0)
sigma1 = np.identity(n)
sigma2 = np.identity(n)
pi = 0.5
# 3. 实现EM算法
for i in range(max_iter):
# a. 初始化多元高斯分布(初始化两个多元高斯混合概率密度函数)
norm1 = multivariate_normal(mu1, sigma1)
norm2 = multivariate_normal(mu2, sigma2)
# E step
# 计算所有样本数据在norm1和norm2中的概率
tau1 = pi * norm1.pdf(x)
tau2 = (1 - pi) * norm2.pdf(x)
# 概率做一个归一化操作
w = tau1 / (tau1 + tau2)
# M step
mu1 = np.dot(w, x) / np.sum(w)
mu2 = np.dot(1 - w, x) / np.sum(1 - w)
sigma1 = np.dot(w * (x - mu1).T, (x - mu1)) / np.sum(w)
sigma2 = np.dot((1 - w) * (x - mu2).T, (x - mu2)) / np.sum(1 - w)
pi = np.sum(w) / m
# 返回最终解
return (pi, mu1, mu2, sigma1, sigma2)
if __name__ == '__main__':
np.random.seed(28)
# 产生一个服从多元高斯分布的数据(标准正态分布的多元高斯数据)
mean1 = (0, 0, 0) # x1\x2\x3的数据分布都是服从正态分布的,同时均值均为0
cov1 = np.diag((1, 1, 1))
data1 = np.random.multivariate_normal(mean=mean1, cov=cov1, size=500)
# 产生一个数据分布不均衡
mean2 = (2, 2, 3)
cov2 = np.array([[1, 1, 3], [1, 2, 1], [0, 0, 1]])
data2 = np.random.multivariate_normal(mean=mean2, cov=cov2, size=200)
# 合并两个数据
data = np.vstack((data1, data2))
pi, mu1, mu2, sigma1, sigma2 = train(data, 100)
print("第一个类别的相关参数:")
print(mu1)
print(sigma1)
print("第二个类别的相关参数:")
print(mu2)
print(sigma2)
print("预测样本属于那个类别(概率越大就是那个类别):")
norm1 = multivariate_normal(mu1, sigma1)
norm2 = multivariate_normal(mu2, sigma2)
x = np.array([0, 1, 0])
print(pi * norm1.pdf(x)) # 属于类别1的概率为:0.0275 => 0.989
print((1 - pi) * norm2.pdf(x))# 属于类别1的概率为:0.0003 => 0.011
HMM详解
隐马尔可夫模型(Hidden Markov Model,HMM)作为一种统计分析模型,创立于20世纪70年代。80
年代得到了传播和发展,成为信号处理的一个重要方向,现已成功地用于语音识别,行为识别,文字识别以及故障诊断等领域。
HMM介绍
HMM是统计模型,它用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数。然后利用这些参数来作进一步的分析,例如模式识别。
马尔可夫性质
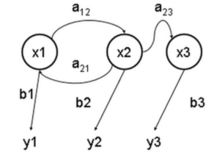
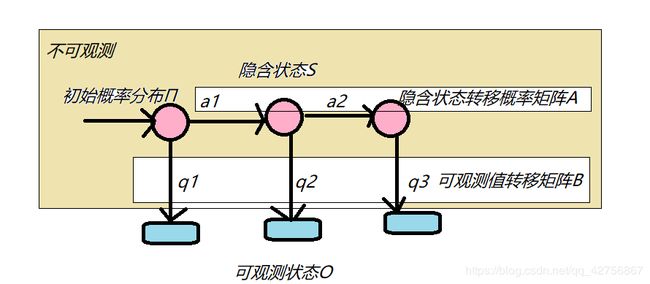
数学定理:设{X(t), t ∈ T}是一个随机过程,E为其状态空间,若对于任意的t1 大致意思就是我们当前状态只受上一状态的影响,而跟上一状态之前的状态无关,就叫做马尔可夫性。 马尔可夫链是指具有马尔可夫性质的随机过程。在过程中,在给定当前信息的情 举个例子来讲: 设将天气状态分为晴、阴、雨三种状态,假定某天的天气状态只和上一天的天气状态有关,状态使用1(晴)、2(阴)、3(雨)表示,转移概率矩阵P如下: 我们再看一下它们的各自转移方式: 假设某天的天气概率只与前一天的概率有关,也就是如下公式: π n + 1 = π n ∗ P π^{n+1}=π^{n}*P πn+1=πn∗P HMM是一种统计模型,在语音识别、行为识别、NLP、故障诊断等领域具有高效的性能。 HMM是关于时序的概率模型,描述一个含有未知参数的马尔可夫链所生成的不可观测的状态随机序列,再由各个状态生成观测随机序列的过程。 HMM是一个双重随机过程—具有一定状态的隐马尔可夫链和随机的观测序列。HMM随机生成的状态随机序列被称为状态序列;每个状态成一个观测,由此产生的观测随机序列,被称为观测序列。 HMM由隐含状态S、可观测状态O、初始状态概率矩阵π、隐含状态转移概率矩阵A、可观测值转移矩阵B(又称为混淆矩阵,Confusion Matrix); 这里Π和A决定了状态序列S,B决定了可观测序列O,所以它们三个式整个隐马的关键: A = [ a i j ] n ∗ n A=[a_{ij}]_{n*n} A=[aij]n∗n B = [ b i j ] n ∗ m B = [b_{ij}]_{n*m} B=[bij]n∗m π = ( π i ) 1 ∗ n = ( π 1 , π 2 , π 3 , . . . , π n ) π = (π_i)_1*n= (π_1,π_2,π_3,...,π_n) π=(πi)1∗n=(π1,π2,π3,...,πn) S = { s 1 , s 2 , s 3 , . . . , s n } S = \{{s_1,s_2,s_3,...,s_n}\} S={s1,s2,s3,...,sn} O = { o 1 , o 2 , o 3 , . . . , o m } O = \{{o_1,o_2,o_3,...,o_m}\} O={o1,o2,o3,...,om} 这里S和O是相对于整个集合而言的,我们一般只会度量前T个状态序列I和观测序列Q: Q = { q 1 , q 2 , . . . , q T } Q= \{q_1,q_2,...,q_T\} Q={q1,q2,...,qT} 这里每个q发生的概率只受i的影响,而每一个i只受前一个i的影响。 假设有三个盒子,编号为1,2,3;每个盒子都装有黑白两种颜色的小球,球的比例如下: 按照下列规则的方式进行有放回的抽取小球,得到球颜色的观测序列: 状态集合:S={盒子1,盒子2,盒子3} 状态转移概率矩阵A: 这时候我们面对自己假设的A,B,π,那它们得到观测序列“白黑白白黑“的概率是多少? 现在假设条件下,唯一未知得就是状态序列,所以这里就要尝试使用不同的状态序列,并找到在一个在估计模型下的拥有最大概率的状态序列。 有了状态序列我们就可以预测再次抽取时发生事件的概率,在这个例子里就是我们每次到底抽的时那个盒子,但是估计模型是假设的所以在去求状态序列的前面,应该先去求得最优得A,B,π使得在这个模型下观测序列发生得概率最大。 这里便出现了两个问题: 1,如何求得一个估计模型,让观测序列在该模型下发生概率最大。 2,如何求得隐藏得状态序列,让它在最优估计模型下发生得概率最大。 这里为什么要求概率最大,便涉及到了最大熵模型。 应用到实际便成了三个问题,就是多一个我们如何该观测序列在估计模型上出现得概率。 给定模型λ=(A,B,π)和观测序列Q={q1,q2,…,qT},计算模型λ下观测到序列Q出现的概率P(Q|λ) 已知观测序列Q={q1,q2,…,qT},估计模型λ=(A,B,π)的参数,使得在该模型下观测序列P(Q|λ)最大。 给定模型λ=(A,B,π)和观测序列Q={q1,q2,…,qT},求给定观测序列条件概率P(I|Q,λ) 前向概率-后向概率指的其实是在一个观测序列中,时刻t对应的状态为si的概率值转换过来的信息。 所以这两种都可以解决概率计算问题,也就是看懂一个就可以继续下一个问题。 首先写出在状态序列为s_i的情况下,观测序列出现的概率。 前向算法定义:给定λ(A,B,π),定义到时刻t部分观测序列为q1,q2,…,qt且状态为si的概率为前向概率。此时我们加设β为1,所以表达方程记做: 初值 先计算第一个α: α 1 ( i ) = P ( q 1 , i 1 = s i ; λ ) = π i b i q 1 \alpha_1(i)=P(q_1,i_1= s_i;\lambda)=π_ib_{iq_1} α1(i)=P(q1,i1=si;λ)=πibiq1 递推 求出第一个后,递推使t = 1,2,…,T-1 结果 这样状态序列为s_i的情况下,观测序列出现的概率就变成了: 后向传播定义:给定λ,定义到时刻t状态为si的前提下,从t+1到T部分观测序列为qt+1,qt+2,…,qT的概率为后向概率。记做: 先计算第一个β,在我们进行前向算法的时候我们假设β为1: β T i = 1 β_T{i} = 1 βTi=1 递推 求出第一个后,递推使t = T-1,T-2…,1 结果 这样状态序列为s_i的情况下,观测序列出现的概率就变成了: 根据概率计算问题我们可以求的两个可以帮助我们解决学习问题的概率: 将给定模型λ和观测序列Q的情况下,在时刻t处于状态si的概率,记做: 推导过程: 将给定模型λ和观测序列Q的情况下,在时刻t处于状态si并且在t+1时刻处于状态sj的概 也就是: P ( i t = s i , i t + 1 = s j , Q ; λ ) = α t ( i ) a i j b j q t + 1 β t + 1 ( j ) P(i_t = s_i,i_{t+1} = s_j,Q;\lambda) = \alpha_t(i)a_{ij}b_{jq_{t+1}}β_{t+1}(j) P(it=si,it+1=sj,Q;λ)=αt(i)aijbjqt+1βt+1(j) 若训练数据包含观测序列和状态序列,则HMM的学习问题非常简单,是监督学 π ^ i = ∣ s i ∣ ∑ i = 1 n ∣ s i j ∣ ) a ^ i j = ∣ s i j ∣ ∑ i = 1 n ∣ s i j ∣ ) b ^ i j = ∣ q i j ∣ ∑ i = 1 n ∣ q i j ∣ ) \hat \pi_i=\frac{|s_i|}{\sum_{i=1}^n|s_{ij}|)}\\ \hat a_{ij}=\frac{|s_{ij}|}{\sum_{i=1}^n|s_{ij}|)}\\ \hat b_{ij}=\frac{|q_{ij}|}{\sum_{i=1}^n|q_{ij}|)}\\ π^i=∑i=1n∣sij∣)∣si∣a^ij=∑i=1n∣sij∣)∣sij∣b^ij=∑i=1n∣qij∣)∣qij∣ 但是我们的训练数据只包含观测序列,则HMM的学习问题需要使用EM算法求解,是非 那么我们想一下,这里假设所有的观测数据为Q={q1,q2,…,qT},所有的隐状态为I={i1,i2,…,iT},则完整的数据为(O,I),完整数据的对数似然函数为ln(p(Q,I;λ)); 然后直接使用EM算法的方式就可以来进行参数估计了。(EM算法不懂见上) 初始化分布参数 重复下列两个操作直到收敛: E步骤:估计隐藏变量的概率分布期望函数: L ( λ , λ ‾ ) = ∑ I l n ( P ( Q , I ; λ ) ) P ( I ∣ Q ; λ ‾ ) = ∑ I l n ( P ( Q , I , λ ) ) p ( I , Q , λ ‾ ) p ( Q , λ ‾ ) → ∑ I l n ( p ( Q , I ; λ ) ) p ( I , Q ; λ ‾ ) L(\lambda,\overline \lambda) = \sum_Iln(P(Q,I;\lambda))P(I|Q;\overline \lambda)\\ =\sum_Iln(P(Q,I,\lambda))\frac{p(I,Q,\overline \lambda)}{p(Q,\overline \lambda)}\\ \to\sum_I ln(p(Q,I;\lambda))p(I,Q;\overline \lambda)\\ L(λ,λ)=I∑ln(P(Q,I;λ))P(I∣Q;λ)=I∑ln(P(Q,I,λ))p(Q,λ)p(I,Q,λ)→I∑ln(p(Q,I;λ))p(I,Q;λ) L ( λ , λ ‾ ) = ∑ I l n ( π i ) p ( I , Q ; λ ‾ ) + ∑ I ( ∑ t = 1 T − 1 l n a i t i t + 1 p ( I , Q ; λ ‾ ) ) + ∑ I ( ∑ t = 1 T l n b i t q t ) p ( I , Q ; λ ‾ ) L(\lambda,\overline \lambda) = \sum_Iln(\pi_i)p(I,Q;\overline \lambda) + \sum_I(\sum_{t=1}^{T-1}ln a_{i_ti_{t+1}}p(I,Q;\overline \lambda))+\sum_I(\sum_{t=1}^Tlnb_{i_tq_t})p(I,Q;\overline \lambda) L(λ,λ)=I∑ln(πi)p(I,Q;λ)+I∑(t=1∑T−1lnaitit+1p(I,Q;λ))+I∑(t=1∑Tlnbitqt)p(I,Q;λ) 当我们了解L函数,也就是我们需要极大化的函数,可以直接对π求导,然后让偏导等于零。 这 里 使 用 拉 格 朗 日 乘 子 法 , 我 们 除 了 要 最 小 化 目 标 函 数 外 , 我 们 还 要 满 足 : ∑ i = 1 n π i = 1 这里使用拉格朗日乘子法,我们除了要最小化目标函数外,我们还要满足:\sum_{i=1}^n\pi_i =1 这里使用拉格朗日乘子法,我们除了要最小化目标函数外,我们还要满足:i=1∑nπi=1 这 时 候 有 了 等 值 约 束 : ∑ i = 1 n l n ( π i ) p ( Q , i 1 = i ; λ ‾ ) + β ( ∑ i = 1 n π i − 1 ) 这时候有了等值约束:\sum_{i=1}^nln(\pi_i)p(Q,i_1 = i;\overline \lambda)+β(\sum_{i=1}^n\pi_i -1) 这时候有了等值约束:i=1∑nln(πi)p(Q,i1=i;λ)+β(i=1∑nπi−1) p ( Q , i 1 = i ; λ ‾ ) + β π i = 0 β = − P ( Q , λ ‾ ) π i = p ( Q , i 1 = i ; λ ‾ ) p ( Q ; λ ‾ ) = p ( Q , i 1 = i ; λ ‾ ) ∑ i = 1 n p ( Q , i 1 = i ; λ ‾ ) = γ 1 ( i ) p(Q,i_1 = i;\overline \lambda) +β\pi_i = 0\\ β = -P(Q,\overline \lambda)\\ \pi_i = \frac{p(Q,i_1 = i;\overline \lambda)}{p(Q;\overline \lambda)}\\ = \frac{p(Q,i_1 = i;\overline \lambda)}{\sum_{i=1}^np(Q,i_1 = i;\overline \lambda)}=\gamma_1(i)\\ p(Q,i1=i;λ)+βπi=0β=−P(Q,λ)πi=p(Q;λ)p(Q,i1=i;λ)=∑i=1np(Q,i1=i;λ)p(Q,i1=i;λ)=γ1(i) 这里写到γ是不是很熟悉,没错就是我们是上面求的单个状态的概率。 和上一个变量求解一样,我们需要极大化L 这 里 我 们 除 了 需 要 满 足 : ∑ i = 1 n ∑ j = 1 n a i j = n 这里我们除了需要满足:\sum_{i=1}^n\sum_{j=1}^na_{ij}=n 这里我们除了需要满足:i=1∑nj=1∑naij=n 等 值 约 束 公 式 : ∑ i = 1 n ∑ j = 1 n ∑ t = 1 T − 1 l n ( a i j p ( Q , i t = i , i t + 1 = j ; λ ‾ ) ) + β ( ∑ i = 1 n ∑ j = 1 n a i j = n ) 等值约束公式:\\\sum_{i=1}^n \sum_{j=1}^n \sum_{t=1}^{T-1}ln(a_{ij}p(Q,i_t = i,i_{t+1}=j;\overline \lambda))+\beta(\sum_{i=1}^n\sum_{j=1}^na_{ij}=n) 等值约束公式:i=1∑nj=1∑nt=1∑T−1ln(aijp(Q,it=i,it+1=j;λ))+β(i=1∑nj=1∑naij=n) 经 过 对 数 似 然 : ∑ t = 1 T − 1 p ( Q , i t = i , i t + 1 = j ; λ ‾ ) ) + β a i j = 0 这 时 候 可 以 求 出 β = − ∑ t = 1 T − 1 p ( Q , i t = i ; λ ‾ ) a i j = ∑ t = 1 T − 1 p ( Q , i t = i , i t + 1 = j ; λ ‾ ) ∑ t = 1 T − 1 p ( Q , i t = i ; λ ‾ ) = ∑ t = 1 T − 1 ξ t ( i , j ) ∑ t = 1 T − 1 γ t ( i ) 经过对数似然: \sum_{t=1}^{T-1}p(Q,i_t = i,i_{t+1}=j;\overline \lambda))+\beta a_{ij}=0\\ 这时候可以求出\beta = -\sum_{t=1}^{T-1}p(Q,i_t = i;\overline \lambda)\\ a_{ij}=\frac{\sum_{t=1}^{T-1}p(Q,i_t = i,i_{t+1}=j;\overline \lambda)}{\sum_{t=1}^{T-1}p(Q,i_t = i;\overline \lambda)}\\ =\frac{\sum_{t=1}^{T-1}\xi_t(i,j)}{\sum_{t=1}^{T-1}\gamma _t(i)} 经过对数似然:t=1∑T−1p(Q,it=i,it+1=j;λ))+βaij=0这时候可以求出β=−t=1∑T−1p(Q,it=i;λ)aij=∑t=1T−1p(Q,it=i;λ)∑t=1T−1p(Q,it=i,it+1=j;λ)=∑t=1T−1γt(i)∑t=1T−1ξt(i,j) 在上面的式子里,我们求aij也就是A的时候,我们必须使用单个状态的概率和两个状态的联合概率。 同上我们对B求偏导,然后让偏导等于零: 这 里 我 们 除 了 需 要 满 足 : ∑ i = 1 n ∑ j = 1 n b i j = n 这里我们除了需要满足:\sum_{i=1}^n\sum_{j=1}^nb_{ij}=n 这里我们除了需要满足:i=1∑nj=1∑nbij=n 等 值 约 束 公 式 : ∑ i = 1 n ∑ j = 1 n ∑ t = 1 T l n b i j P ( Q , i t = i , i t + 1 = j ; λ ‾ ) + β ( ∑ i = 1 n ∑ j = 1 n b i j − n ) 经 过 对 数 似 然 : ∑ t = 1 T − 1 p ( Q , i t = i , i t + 1 = j ; λ ‾ ) ) + β b i j = 0 这 时 候 可 以 求 出 β = − ∑ t = 1 T − 1 p ( Q , i t = i ; λ ‾ ) b i j = ∑ t = 1 T p ( Q , i t = i , i t + 1 = j ; λ ‾ ) ∑ t = 1 T p ( Q , i t = i ; λ ‾ ) = ∑ t = 1 , q t = j T p ( Q , i t = i ; λ ‾ ) ∑ t = 1 T p ( Q , i t = i ; λ ‾ ) = ∑ t = 1 , q t = j T γ t ( i ) ∑ t = 1 T γ t ( i ) 等值约束公式:\\ \sum_{i=1}^n \sum_{j=1}^n\sum_{t=1}^Tlnb_{ij}P(Q,i_t = i,i_{t+1}=j;\overline \lambda)+\beta(\sum_{i=1}^n\sum_{j=1}^nb_{ij}-n)\\ 经过对数似然: \sum_{t=1}^{T-1}p(Q,i_t = i,i_{t+1}=j;\overline \lambda))+\beta b_{ij}=0\\ 这时候可以求出\beta = -\sum_{t=1}^{T-1}p(Q,i_t = i;\overline \lambda)\\ b_{ij}=\frac{\sum_{t=1}^{T}p(Q,i_t = i,i_{t+1}=j;\overline \lambda)}{\sum_{t=1}^{T}p(Q,i_t = i;\overline \lambda)}\\ =\frac{\sum_{t=1,q_t = j}^{T}p(Q,i_t = i;\overline \lambda)}{\sum_{t=1}^{T}p(Q,i_t = i;\overline \lambda)}\\ =\frac{\sum_{t=1,q_t=j}^{T}\gamma _t(i)}{\sum_{t=1}^{T}\gamma _t(i)} 等值约束公式:i=1∑nj=1∑nt=1∑TlnbijP(Q,it=i,it+1=j;λ)+β(i=1∑nj=1∑nbij−n)经过对数似然:t=1∑T−1p(Q,it=i,it+1=j;λ))+βbij=0这时候可以求出β=−t=1∑T−1p(Q,it=i;λ)bij=∑t=1Tp(Q,it=i;λ)∑t=1Tp(Q,it=i,it+1=j;λ)=∑t=1Tp(Q,it=i;λ)∑t=1,qt=jTp(Q,it=i;λ)=∑t=1Tγt(i)∑t=1,qt=jTγt(i) 经过极大化L函数我们可以求得π、a、b的值,这样我们便得到了一个最优模型。 π i = γ 1 ( i ) a i j = ∑ t = 1 T − 1 ξ t ( i , j ) ∑ t = 1 T − 1 γ t ( i ) b i j = ∑ t = 1 , q t = j T γ t ( i ) ∑ t = 1 T γ t ( i ) \pi_i = \gamma_1(i)\space\space\space\space\space\space\space a_{ij} = \frac{\sum_{t=1}^{T-1}\xi_t(i,j)}{\sum_{t=1}^{T-1}\gamma _t(i)}\space\space\space\space\space\space b_{ij} =\frac{\sum_{t=1,q_t=j}^{T}\gamma _t(i)}{\sum_{t=1}^{T}\gamma _t(i)} πi=γ1(i) aij=∑t=1T−1γt(i)∑t=1T−1ξt(i,j) bij=∑t=1Tγt(i)∑t=1,qt=jTγt(i) Viterbi算法实际是用动态规划的思路求解HMM预测问题,求出概率最大的“路径”,每条“路径”对应一个状态序列。 动态规划是运筹学的一个分支,是求解决策过程最优化的数学方法。 比如斐波那契数列和背包问题都利用了这个思想。 σ t ( i ) = max i 1 , i 2 . . . i t − 1 p ( i t = i , i 1 , i 2 . . . i t − 1 , q t , q t − 1 . . . q 1 ; λ ) σ 1 ( i ) = π i b i q 1 σ t + 1 ( i ) = max 1 ≤ i ≤ n ( σ t ( j ) a j i ) b i q t + 1 当 求 出 max 1 ≤ i ≤ n σ T ( i ) 便 求 出 了 最 大 概 率 。 \sigma_t(i) = \max_{i_1,i_2...i_{t-1}}p(i_t = i,i_1,i_2...i_{t-1},q_t,q_{t-1}...q_1;\lambda)\\ \sigma_1(i) = \pi_ib_{iq_1}\\ \sigma_{t+1}(i) = \max_{1\le i\le n}(\sigma_t(j)a_{ji})b_{iq_{t+1}}\\ 当求出 \max_{1\le i \le n}\sigma_{T}(i)便求出了最大概率。 σt(i)=i1,i2...it−1maxp(it=i,i1,i2...it−1,qt,qt−1...q1;λ)σ1(i)=πibiq1σt+1(i)=1≤i≤nmax(σt(j)aji)biqt+1当求出1≤i≤nmaxσT(i)便求出了最大概率。 隐马尔可夫模型(HMM)是由马尔可夫过程衍生出的概率图模型,常被用于语音模式识别、生物基因序列标记、金融时间序列预测等。 HMM在我们生活中无处不在,举个简单的例子: 身边的朋友一般出行有骑共享单车出行的,说下雨就比晴天骑车的人数少,当我们听朋友说今天外面共享单车被骑没了,我们可以推断出今天天气不错,这里显式状态是出行,而隐状态是天气。 所以我们很早就已经会HMM算法的思想了,只是差这几个算法和证明。 这里说的HMM不是买零食的韩梅梅 时间点 t的隐藏条件和时间点 t-1的隐藏条件有关。 因为人类语音拥有前后的关系,可以从语义与发音两点来看: 单字的发音拥有前后关系:例如"They are"常常发音成"They’re",或是"Did you"会因为"you"的发音受"did"的影响,常常发音成"did ju",而且语音识别中用句子的发音来进行分析,因此需要考虑到每个音节的前后关系,才能够有较高的准确率。 句子中的单字有前后关系:从英文文法来看,主词后面常常接助动词或是动词,动词后面接的会是受词或介系词。而或是从单一单字的使用方法来看,对应的动词会有固定使用的介系词或对应名词。因此分析语音频息时需要为了提升每个单字的准确率,也需要分析前后的单字。 马尔可夫模型将输入消息视为一单位一单位,接着进行分析,与人类语音模型的特性相似。语音系统识别的单位为一个单位时间内的声音。利用梅尔倒频谱等语音处理方法,转换成一个发音单位,为离散型的信息。而马尔可夫模型使用的隐藏条件也是一个个被数据包的 x(t),因此使用马尔可夫模型来处理声音频号比较合适。马尔可夫链
况下,过去的信息状态对于预测将来状态是无关的。
在马尔可夫链的每一步,系统根据概率分布,可以从一个状态变成另外一个状态,也可以保持当前状态不变。状态的改变叫做转移,状态改变的相关概率叫做转移概率。
马尔可夫链中的三元素是:状态空间S、转移概率矩阵P、初始概率分布π。
下面我们开始迭代,首先假设第一天的初始概率Π=[0.5,0.3,0.2],由上式和P矩阵迭代: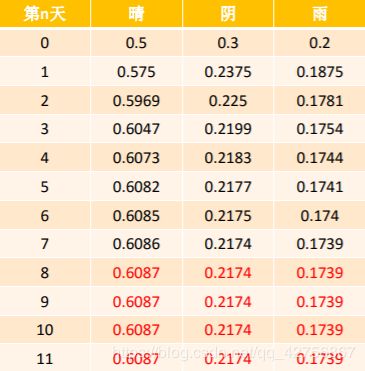
这里重新假设第一天的初始概率π=[0.1,0.6,0.3],由上式和P矩阵迭代:
由此得出规律,只要迭代次数够多,我们初始概率π并不会影响最终概率的出现。隐马尔科夫模型
λ = ( π , A , B ) λ=(π,A,B) λ=(π,A,B)
I = { i 1 , i 2 , . . . , i T } I= \{i_1,i_2,...,i_T\} I={i1,i2,...,iT}HMM案例
编号
白球
黑球
1
4
6
2
8
2
3
5
5
观测集合:O={白,黑}
设状态序列和观测序列的长度T=5,并假设如下A,B,π
A = ( 0.5 0.4 0.1 0.2 0.2 0.6 0.2 0.5 0.3 ) A=\begin{pmatrix} 0.5&0.4&0.1\\ 0.2&0.2&0.6\\ 0.2&0.5&0.3\\ \end{pmatrix} A=⎝⎛0.50.20.20.40.20.50.10.60.3⎠⎞
观测概率矩阵B:
B = ( 0.4 0.6 0.8 0.2 0.5 0.5 ) B=\begin{pmatrix} 0.4&0.6\\ 0.8&0.2\\ 0.5&0.5\\ \end{pmatrix} B=⎝⎛0.40.80.50.60.20.5⎠⎞
初始概率分布π:
π = ( 0.2 0.5 0.3 ) π=\begin{pmatrix} 0.2\\ 0.5\\ 0.3\\ \end{pmatrix} π=⎝⎛0.20.50.3⎠⎞
三个问题
概率计算问题:前向-后向算法
学习问题:Baum-Welch算法(状态未知)
预测问题:Viterbi算法
最大的状态序列I概率计算问题(前后向)

P ( q 1 , q 2 . . . q T , i t = s i ) = P ( q 1 , q 2 . . . q t = s i ) P ( q t + 1 , q t + 2 . . . q T ∣ q 1 , q 2 , . . . , q t , i t = s i ) = P ( q 1 , q 2 . . . q t = s i ) P ( q t + 1 , q t + 2 . . . q T , i t = s i ) P(q_1,q_2...q_T,i_t = s_i) = P(q_1,q_2...q_t = s_i) P(q_{t+1},q_{t+2}...q_T|q_1,q_2,...,q_t,i_t = s_i) \\=P(q_1,q_2...q_t = s_i) P(q_{t+1},q_{t+2}...q_T,i_t = s_i) P(q1,q2...qT,it=si)=P(q1,q2...qt=si)P(qt+1,qt+2...qT∣q1,q2,...,qt,it=si)=P(q1,q2...qt=si)P(qt+1,qt+2...qT,it=si)
这 里 我 们 把 这 一 部 分 称 为 β = P ( q t + 1 , q t + 2 . . . q T , i t = s i ) 这 里 我 们 把 这 一 部 分 称 为 α = P ( q 1 , q 2 . . . q t = s i ) 这里我们把这一部分称为β = P(q_{t+1},q_{t+2}...q_T,i_t = s_i)\\ 这里我们把这一部分称为α = P(q_1,q_2...q_t = s_i) 这里我们把这一部分称为β=P(qt+1,qt+2...qT,it=si)这里我们把这一部分称为α=P(q1,q2...qt=si)
α t ( i ) = P ( q 1 , q 2 . . . q t , i t = s i ; λ ) \alpha_t(i)=P(q_1,q_2...q_t ,i_t= s_i;\lambda) αt(i)=P(q1,q2...qt,it=si;λ)
α t + 1 ( i ) = ( ∑ j = 1 n α t ( j ) α j i ) b i q t + 1 \alpha_{t+1}(i)=(\sum_{j=1}^n\alpha_t(j)\alpha_{ji})b_{iq_{t+1}} αt+1(i)=(j=1∑nαt(j)αji)biqt+1

α t ( i ) = P ( q 1 , q 2 . . . q t , i t = s i ) = P ( q 1 , q 2 . . . q t − 1 , i t = s i ) ∗ P ( q t , i t = s i ) = [ ∑ j = 1 n P ( q 1 , q 2 . . . q t − 1 , i t − 1 = s j , i t = s i ) ] ∗ P ( q t ∣ i t = s i ) = [ ∑ j = 1 n P ( q 1 , q 2 . . . q t − 1 , i t − 1 = s j ) P ( i t = s i ∣ i t − 1 = s j ) ] ∗ P ( q t ∣ i t = s i ) = ( ∑ j = 1 n α t − 1 a j i ) b i q t \alpha_t(i)=P(q_1,q_2...q_t ,i_t= s_i)\\ =P(q_1,q_2...q_{t-1},i_t= s_i)*P(q_t ,i_t= s_i)\\ =[\sum_{j=1}^nP(q_1,q_2...q_{t-1} ,i_{t-1}= s_j,i_t = s_i)]*P(q_t|i_t = s_i)\\ =[\sum_{j=1}^nP(q_1,q_2...q_{t-1} ,i_{t-1}= s_j)P(i_t = s_i|i_{t-1}= s_j)]*P(q_t|i_t = s_i)\\ =(\sum_{j=1}^n\alpha_{t-1}a_{ji})b_{iq_t} αt(i)=P(q1,q2...qt,it=si)=P(q1,q2...qt−1,it=si)∗P(qt,it=si)=[j=1∑nP(q1,q2...qt−1,it−1=sj,it=si)]∗P(qt∣it=si)=[j=1∑nP(q1,q2...qt−1,it−1=sj)P(it=si∣it−1=sj)]∗P(qt∣it=si)=(j=1∑nαt−1aji)biqt
P ( Q ; λ ) = ∑ i = 1 n α T ( i ) P(Q;\lambda) = \sum_{i=1}^n\alpha_T(i) P(Q;λ)=i=1∑nαT(i)
[前向传播代码]: https://github.com/TimVerion/HMM_code/blob/master/hmm/forward_probability.py “前向传播代码”# 伪代码,不可运行
# 更新初值(t=1)
for i in n_range:
alpha[0][i] = pi[i] * B[i][fetch_index_by_obs_seq_f(Q, 0)]
# 迭代更新其它时刻
T = len(Q)
tmp = [0 for i in n_range]
for t in range(1, T):
for i in n_range:
# 1. 计算上一个时刻t-1累积过来的概率值
for j in n_range:
tmp[j] = alpha[t - 1][j] * A[j][i]
# 2. 更新alpha的值
alpha[t][i] = np.sum(tmp) * B[i][fetch_index_by_obs_seq_f(Q, t)]
β t ( i ) = P ( q t + 1 , q t + 2 . . . q T ∣ i t = s i ; λ ) β_t(i)=P(q_{t+1},q_{t+2}...q_T | i_t= s_i;\lambda) βt(i)=P(qt+1,qt+2...qT∣it=si;λ)
1. 初值
β t ( i ) = ( ∑ j = 1 n α i j b j q ( t + 1 ) β t + 1 ( j ) ) β_t(i)=(\sum_{j=1}^n\alpha_{ij}b_{jq_(t+1)}β_{t+1}(j)) βt(i)=(j=1∑nαijbjq(t+1)βt+1(j))

β t ( i ) = P ( q t + 1 , q t + 2 . . . q T , i t = s i ) = ∑ j = 1 n P ( i t + 1 = s j , q t + 1 , q t + 2 . . . q T ∣ i t = s i ) = ∑ j = 1 n P ( q t + 1 , q t + 2 . . . q T ∣ i t + 1 = s j ) P ( i t + 1 = s j ∣ i t = s i ) = ∑ j = 1 n P ( q t + 2 . . . q T ∣ i t + 1 = s j ) P ( q t + 1 ∣ i t + 1 = s j ) P ( i t + 1 = s j ∣ i t = s i ) = ∑ j = 1 n ( β t + 1 ( j ) b j q t + 1 a i j ) β_t(i)=P(q_{t+1},q_{t+2}...q_T ,i_t= s_i)\\ =\sum_{j=1}^nP(i_{t+1} = s_j,q_{t+1},q_{t+2}...q_T|i_t = s_i)\\ =\sum_{j=1}^nP(q_{t+1},q_{t+2}...q_T|i_{t+1} = s_j)P(i_{t+1} = s_j|i_t = s_i)\\ =\sum_{j=1}^nP(q_{t+2}...q_T|i_{t+1} = s_j)P(q_{t+1}|i_{t+1} =s_j)P(i_{t+1} = s_j|i_t = s_i)\\ =\sum_{j=1}^n(β_{t+1}(j)b_{jq_{t+1}}a_{ij}) βt(i)=P(qt+1,qt+2...qT,it=si)=j=1∑nP(it+1=sj,qt+1,qt+2...qT∣it=si)=j=1∑nP(qt+1,qt+2...qT∣it+1=sj)P(it+1=sj∣it=si)=j=1∑nP(qt+2...qT∣it+1=sj)P(qt+1∣it+1=sj)P(it+1=sj∣it=si)=j=1∑n(βt+1(j)bjqt+1aij)
P ( Q ; λ ) = ∑ i = 1 n π i b i q 1 β 1 ( i ) P(Q;\lambda) = \sum_{i=1}^nπ_ib_{iq_1}β_1(i) P(Q;λ)=i=1∑nπibiq1β1(i)# 更新初值(t=T)
for i in n_range:
beta[T - 1][i] = 1
# 迭代更新其它时刻
tmp = [0 for i in n_range]
for t in range(T - 2, -1, -1):
for i in n_range:
# 1. 计算到下一个时刻t+1的概率值
for j in n_range:
tmp[j] = A[i][j] * beta[t + 1][j] * B[j][fetch_index_by_obs_seq_f(Q, t +1)]
# 2. 更新beta的值
beta[t][i] = np.sum(tmp)
学习问题(鲍姆韦尔奇)
1,单个状态的概率
γ t ( i ) = p ( i t = s i ∣ Q ; λ ) γ_t(i) = p(i_t = s_i|Q;\lambda) γt(i)=p(it=si∣Q;λ)
单个状态概率的意义主要是用于判断在每个时刻最可能存在的状态,从而可以得
到一个状态序列作为最终的预测结果。
p ( i t = s i , Q , ; λ ) = α t ( i ) β t ( i ) γ t ( i ) = p ( i t = s i ∣ Q ; λ ) = p ( i t = s i ∣ Q ; λ ) p ( Q ; λ ) = α t ( i ) β t ( i ) ∑ j = 1 n α t ( j ) β t ( j ) p(i_t = s_i,Q,;\lambda) = \alpha_t(i)\beta_t(i)\\ γ_t(i) = p(i_t = s_i|Q;\lambda)\\ =\frac{ p(i_t = s_i|Q;\lambda)}{p(Q;\lambda)}\\ = \frac{\alpha_t(i)\beta_t(i)}{\sum_{j=1}^n\alpha_t(j)\beta_t(j)} p(it=si,Q,;λ)=αt(i)βt(i)γt(i)=p(it=si∣Q;λ)=p(Q;λ)p(it=si∣Q;λ)=∑j=1nαt(j)βt(j)αt(i)βt(i)2,两个状态的联合概率
率,记做:
ξ t ( i , j ) = p ( i t = s i , i t + 1 = s j ∣ Q ; λ ) = p ( i t = s i , i t + 1 = s j , Q ; λ ) P ( Q ; λ ) = p ( i t = s i , i t + 1 = s j , Q ; λ ) ∑ i = 1 n ∑ j = 1 n p ( i t = s i , i t + 1 = s j , Q ; λ ) \xi_t(i,j) = p(i_t = s_i,i_{t+1} = s_j|Q;\lambda)\\ =\frac{p(i_t = s_i,i_{t+1}=s_j,Q;\lambda)}{P(Q;\lambda)}\\ =\frac{p(i_t = s_i,i_{t+1}=s_j,Q;\lambda)}{\sum_{i=1}^n\sum_{j=1}^np(i_t = s_i,i_{t+1}=s_j,Q;\lambda)}\\ ξt(i,j)=p(it=si,it+1=sj∣Q;λ)=P(Q;λ)p(it=si,it+1=sj,Q;λ)=∑i=1n∑j=1np(it=si,it+1=sj,Q;λ)p(it=si,it+1=sj,Q;λ)3,解决学习问题
习算法。我们甚至在知道观测序列和状态序列的时候我们可以利用大数定理求出最优模型。
监督学习算法,这里使用的EM算法也叫做鲍姆韦尔奇。
P ( O , I ; λ ) = π i 1 b i 1 q 1 a i 1 i 2 b i 2 q 2 . . . a i T − 1 i T b i T q T P(O,I;\lambda) = \pi_{i_1}b_{i_1q_1}a_{i_1i_2}b_{i_2q_2}...a_{i_{T-1}i_T}b_{i_Tq_T} P(O,I;λ)=πi1bi1q1ai1i2bi2q2...aiT−1iTbiTqTM步骤:根据期望函数重新估计分布参数
π的求解
∑ I l n ( π I i ) P ( I , Q ; λ ‾ ) = ∑ i = 1 n l n ( π i ) p ( Q , i 1 = i ; λ ‾ ) \sum_Iln(\pi_{I_i})P(I,Q;\overline \lambda) = \sum_{i=1}^nln(\pi_i)p(Q,i_1 = i;\overline \lambda)\\ I∑ln(πIi)P(I,Q;λ)=i=1∑nln(πi)p(Q,i1=i;λ)A的求解
∑ I ( ∑ t = 1 T − 1 l n a i t a t + 1 ) P ( I , Q ; λ ‾ ) = ∑ i = 1 n ∑ j = 1 n ∑ t = 1 T − 1 l n ( a i j p ( Q , i t = i , i t + 1 = j ; λ ‾ ) ) \sum_I(\sum_{t=1}^{T-1}ln a_{i_t}a_{t+1})P(I,Q;\overline \lambda)\\ = \sum_{i=1}^n \sum_{j=1}^n \sum_{t=1}^{T-1}ln(a_{ij}p(Q,i_t = i,i_{t+1}=j;\overline \lambda)) I∑(t=1∑T−1lnaitat+1)P(I,Q;λ)=i=1∑nj=1∑nt=1∑T−1ln(aijp(Q,it=i,it+1=j;λ))B的求解
∑ I ( ∑ t = 1 T − 1 l n b i t q t ) P ( I , Q ; λ ‾ ) = ∑ i = 1 n ∑ j = 1 n ∑ t = 1 T l n b i j P ( Q , i t = i , i t + 1 = j ; λ ‾ ) \sum_I(\sum_{t=1}^{T-1}ln b_{i_tq_t})P(I,Q;\overline \lambda)\\ = \sum_{i=1}^n \sum_{j=1}^n\sum_{t=1}^Tlnb_{ij}P(Q,i_t = i,i_{t+1}=j;\overline \lambda) I∑(t=1∑T−1lnbitqt)P(I,Q;λ)=i=1∑nj=1∑nt=1∑TlnbijP(Q,it=i,it+1=j;λ)# 1. 迭代更新(EM算法思想类型)
for time in range(max_iter):
# a. 在当前的pi,A,B的情况下对观测序列Q分别计算alpha、beta、gamma和ksi
forward.calc_alpha(pi, A, B, Q, alpha, fetch_index_by_obs_seq_f)
backward.calc_beta(pi, A, B, Q, beta, fetch_index_by_obs_seq_f)
single.calc_gamma(alpha, beta, gamma)
continuous.calc_ksi(alpha, beta, A, B, Q, ksi, fetch_index_by_obs_seq
# b. 更新pi、A、B的值
# b.1. 更新pi值
for i in n_range:
pi[i] = gamma[0]
# b.2. 更新状态转移矩阵A的值
tmp1 = np.zeros(T - 1)
tmp2 = np.zeros(T - 1)
for i in n_range:
for j in n_range:
# 获取所有时刻从状态i转移到状态j的值
for t in t_1_range:
tmp1[t] = ksi[t][i][j]
tmp2[t] = gamma[t]
# 更新状态i到状态j的转移概率
A[i][j] = np.sum(tmp1) / np.sum(tm
# b.3. 更新状态和观测值之间的转移矩阵
for i in n_range:
for k in m_range:
tmp1 = np.zeros(T)
tmp2 = np.zeros(T)
# 获取所有时刻从状态i转移到观测值k的概率和
number = 0
for t in t_range:
if k == fetch_index_by_obs_seq_f(Q, t):
如果序列Q中时刻t对应的观测值就是k,那么进行统计这个时刻t为状态i的概率值
tmp1[t] = gamma[t][i]
number +
tmp2[t] = gamma[t]
# 更新状态i到观测值k之间的转移概率
if number == 0:
# 没有转移,所以为0
B[i][k] = 0
else:
# 有具体值,那么进行更新操作
B[i][k] = np.sum(tmp1) / np.sum(tem2)
预测问题(维特比)
把多阶段过程转化为一系列单阶段问题,利用各阶段之间的关系,逐个求解。# 1. 计算t=1的时候delta的值
for i in n_range:
delta[0][i] = pi[i] * B[i][fetch_index_by_obs_seq_f(Q, 0)]
# 2. 更新其它时刻的值
for t in range(1, T):
for i in n_range:
# 当前时刻t的状态为i
# a. 获取最大值
max_delta = -1
for j in n_range:
# j表示的是上一个时刻的状态值
tmp = delta[t - 1][j] * A[j][i]
if tmp > max_delta:
max_delta = tmp
pre_index[t][i] = j
# b. 更新值
delta[t][i] = max_delta * B[i][fetch_index_by_obs_seq_f(Q, t)]
# 3. 解码操作,查找到最大的结果值
decode = [-1 for i in range(T)]
马尔可夫模型解决语音识别