hill密码（希尔密码）

简述

希尔密码是利用矩阵进行加密的一种加密算法，其本质是一种多表代换密码。

• 百科：
  希尔密码是运用基本矩阵论原理的替换密码，由Lester S. Hill在1929年发明。
  每个字母当作26进制数字：A=0, B=1, C=2… 一串字母当成n维向量，跟一个n×n的矩阵相乘，再将得出的结果模26。
  注意用作加密的矩阵（即密匙）在 必须是可逆的，否则就不可能解码。只有矩阵的行列式和26互质，才是可逆的。

希尔密码由于采用矩阵运算加密，因此在相同的明文加密时，可能会出现不同的密文，因此可以很好的抵御字母频率攻击法。

加解密

• 加密：

1、定义一个矩阵a（须存在逆矩阵）作为加密密钥：

[1，2，1]
[0，2，1]
[1，0，2]

2、将需要加密的明文字母转换为其对应的字母表数字（1-a，2-b……）；
3、将转换后的明文数字序列按照密钥矩阵的阶数进行分组（如本次为3个字符一组）；
4、每组数字序列和密钥矩阵进行矩阵的乘法运算（1x3 矩阵乘以 3x3矩阵），结果即为密文数字序列；
5、可将密文数字序列转换为其对应字母，即为密文字符串。

• 解密：

解密流程与加密相同，唯一不同之处在于：需先求出加密密钥的逆矩阵

在做矩阵相成时，用密文分组乘以逆矩阵，结果即为明文

代码实现

#!/usr/bin/python3.7
# -*- coding: utf-8 -*-
# @Time    : 2019/12/11 14:53
# @Author  : SystemDefenser
# @Email   : [email protected]
# @Software: PyCharm

from numpy import linalg

# 输入矩阵并判断是否存在逆矩阵
def inputMatrix():
    while True:
        # 输入一行、作为行列式的阶数和行列式的第一行
        rank = list(input("").split())
        matrix = [[0] * len(rank) for i in range(len(rank))]
        matrix[0] = rank
        # 输入行列式剩余数据
        for i in range(1, len(matrix)):
            matrix[i] = list(input("").split())
            # 判断每一行输入是否合法
            if len(matrix[i]) != len(matrix):
                print("输入有误，重新输入。")
                continue
        # 转换字符型为整型
        for i in range(len(matrix)):
            matrix[i] = list(map(lambda x: int(x), matrix[i]))
        # 判断是否存在逆矩阵
        if not judgeInverse(matrix):
            print("矩阵不存在逆矩阵，重新输入。")
            continue
        return matrix

# 判断是否存在逆元
def judgeInverse(matrix):
    try:
        linalg.inv(matrix)
    except:
        return False
    return True

# 生成密钥(矩阵的逆矩阵)
def createMatrixInverse(matrix):
    try:
        matrix_inverse = linalg.inv(matrix)
    except:
        return -1
    return matrix_inverse

# 生成消息分组
def createMassageList(massage, matrix):
    matrixRank = len(matrix)
    massageList = []
    # 扩充消息序列并创建分组
    while len(massage) % matrixRank != 0:
        massage += " "
    for i in range(1, len(massage) + 1, matrixRank):
        massageList.append(massage[i-1:i + matrixRank - 1])
    return massageList

# 字母序列转化为数字
def letterToDigit(massageList):
    massageDigitList = []  # 替换后的数字列表
    letterList = []  # 字母列表
    for i in range(ord("a"), ord("z") + 1):
        letterList.append(chr(i))
    for i in range(10):
        letterList.append(str(i))
    # 添加空格，解决分组填充问题
    letterList.append(" ")
    # 替换字母为数字
    for massage in massageList:
        listTmp = []
        for i in range(len(massage)):
            listTmp.append(letterList.index(massage[i]))
        massageDigitList.append(listTmp)
    return massageDigitList

# 数字序列转化为字母
def digitToLetter(massageList):
    massageLetterList = []  # 还原后的字母列表
    letterList = []
    for i in range(ord("a"), ord("z") + 1):
        letterList.append(chr(i))
    for i in range(10):
        letterList.append(str(i))
    letterList.append(" ")
    # 替换数字为字母
    for massage in massageList:
        massageLetterList.append(letterList[massage % 37])
    return massageLetterList

# 加密
def encrypt(massage, matrix):
    ciphertextList = [] # 加密结果列表
    massageList = createMassageList(massage, matrix)
    massageDigitList = letterToDigit(massageList)
    # 矩阵相乘
    for massageDigit in massageDigitList:
        for i in range(len(massageDigit)):
            sum = 0
            for j in range(len(massageDigit)):
                sum += massageDigit[j] * matrix[j][i % len(matrix)]
            ciphertextList.append(sum % 37)
    return ciphertextList

# 解密
def decrypt(massage, matrix):
    plaintextList = []  # 解密结果列表
    matrix_inverse = createMatrixInverse(matrix)
    massageList = createMassageList(massage, matrix)
    # 矩阵相乘
    for msg in massageList:
        for i in range(len(msg)):
            sum = 0
            for j in range(len(msg)):
                sum += msg[j] * matrix_inverse[j][i % len(matrix)]
            plaintextList.append(sum % 37)
    # 浮点型转换为整型(采用四舍五入——round())
    plaintextList = list(map(lambda x: int(round(x)), plaintextList))
    plaintextList = digitToLetter(plaintextList)    # 数字转换为字母
    plaintext = ""
    for item in plaintextList:
        plaintext += item
    return plaintext

if __name__ == "__main__":
    while True:
        print("—————希尔密码—————")
        choice = input("1、加密        2、解密\n请选择：")
        if choice == "1":
            print("输入矩阵：")
            matrix = inputMatrix()
            massage = input("输入msg：")
            massageList = createMassageList(massage, matrix)
            ciphertextList = encrypt(massage, matrix)
            print("加密结果：", ciphertextList)
        elif choice == "2":
            massageList = list(map(int, list(input("输入密文序列：").split(","))))
            print("输入矩阵：")
            matrix = inputMatrix()
            matrix_inverse = createMatrixInverse(matrix)
            print("逆矩阵：")
            for item in matrix_inverse:
                print(item)
            plaintext = decrypt(massageList, matrix)
            print("解密结果：", plaintext)

其中，求逆矩阵部分未能手算，调用了numpy库中的linalg函数，惭愧………………

加密测试

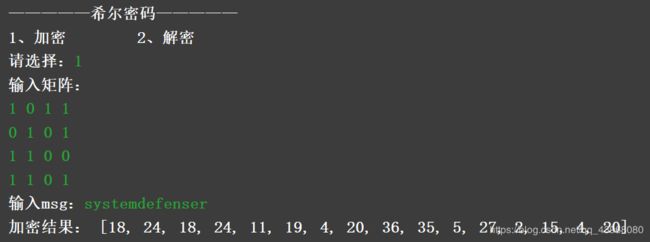
—————希尔密码—————
1、加密        2、解密
请选择：1
输入矩阵：
1 0 1 1
0 1 0 1
1 1 0 0
1 1 0 1
输入msg：systemdefenser
加密结果： [18, 24, 18, 24, 11, 19, 4, 20, 36, 35, 5, 27, 2, 15, 4, 20]
—————希尔密码—————
1、加密        2、解密
请选择：2
输入密文序列：18, 24, 18, 24, 11, 19, 4, 20, 36, 35, 5, 27, 2, 15, 4, 20
输入矩阵：
1 0 1 1
0 1 0 1
1 1 0 0
1 1 0 1
逆矩阵：
[ 0. -1.  0.  1.]
[ 0.  1.  1. -1.]
[ 1.  1.  1. -2.]
[ 0.  0. -1.  1.]
解密结果： systemdefenser 

• 加密：

• 解密：

部分代码详解

• 输入矩阵部分

代码片段：

while True:
        # 输入一行、作为行列式的阶数和行列式的第一行
        rank = list(input("").split())
        matrix = [[0] * len(rank) for i in range(len(rank))]
        matrix[0] = rank
        # 输入行列式剩余数据
        for i in range(1, len(matrix)):
            matrix[i] = list(input("").split())
            # 判断每一行输入是否合法
            if len(matrix[i]) != len(matrix):
                print("输入有误，重新输入。")
                continue

该片段位于 inputMatrix() 函数中。

输入矩阵部分未让用户先定义阶数，而是通过用户输入的矩阵第一行，来决定本次迷药矩阵的阶数，并且不断进行合法判断。

• 解密部分

代码片段：

 # 浮点型转换为整型(采用四舍五入——round())
    plaintextList = list(map(lambda x: int(round(x)), plaintextList))
    plaintextList = digitToLetter(plaintextList)    # 数字转换为字母

该片段位于 decrypt(massage, matrix) 函数中。

由于逆矩阵存在不可约分或整除的小数，因此在此处采用四舍五入round(x) 的方法不严谨地解决此问题。