GRAH ATTENTION NETWORKS
GCN简介
GCN回顾
GAT文章主要是为了解决GCN需要已知整个图才能训练的缺陷而产生。
GAT的实现过程
1、特征提取
与GCN基本相同
import numpy as np
import scipy.sparse as sp
import torch
def encode_onehot(labels):
classes = set(labels)
classes_dict = {c: np.identity(len(classes))[i, :] for i, c in enumerate(classes)}
labels_onehot = np.array(list(map(classes_dict.get, labels)), dtype=np.int32)
return labels_onehot
def load_data(path="./data/cora/", dataset="cora"):
"""Load citation network dataset (cora only for now)"""
print('Loading {} dataset...'.format(dataset))
idx_features_labels = np.genfromtxt("{}{}.content".format(path, dataset), dtype=np.dtype(str))
features = sp.csr_matrix(idx_features_labels[:, 1:-1], dtype=np.float32)
labels = encode_onehot(idx_features_labels[:, -1])
# build graph
idx = np.array(idx_features_labels[:, 0], dtype=np.int32)
idx_map = {j: i for i, j in enumerate(idx)}
edges_unordered = np.genfromtxt("{}{}.cites".format(path, dataset), dtype=np.int32)
edges = np.array(list(map(idx_map.get, edges_unordered.flatten())), dtype=np.int32).reshape(edges_unordered.shape)
adj = sp.coo_matrix((np.ones(edges.shape[0]), (edges[:, 0], edges[:, 1])), shape=(labels.shape[0], labels.shape[0]), dtype=np.float32)
# build symmetric adjacency matrix
adj = adj + adj.T.multiply(adj.T > adj) - adj.multiply(adj.T > adj)
features = normalize_features(features)
adj = normalize_adj(adj + sp.eye(adj.shape[0]))
idx_train = range(140)
idx_val = range(200, 500)
idx_test = range(500, 1500)
adj = torch.FloatTensor(np.array(adj.todense()))
features = torch.FloatTensor(np.array(features.todense()))
labels = torch.LongTensor(np.where(labels)[1])
idx_train = torch.LongTensor(idx_train)
idx_val = torch.LongTensor(idx_val)
idx_test = torch.LongTensor(idx_test)
return adj, features, labels, idx_train, idx_val, idx_test
def normalize_adj(mx):
"""Row-normalize sparse matrix"""
rowsum = np.array(mx.sum(1))
r_inv_sqrt = np.power(rowsum, -0.5).flatten()
r_inv_sqrt[np.isinf(r_inv_sqrt)] = 0.
r_mat_inv_sqrt = sp.diags(r_inv_sqrt)
return mx.dot(r_mat_inv_sqrt).transpose().dot(r_mat_inv_sqrt)
def normalize_features(mx):
"""Row-normalize sparse matrix"""
rowsum = np.array(mx.sum(1))
r_inv = np.power(rowsum, -1).flatten()
r_inv[np.isinf(r_inv)] = 0.
r_mat_inv = sp.diags(r_inv)
mx = r_mat_inv.dot(mx)
return mx
def accuracy(output, labels):
preds = output.max(1)[1].type_as(labels)
correct = preds.eq(labels).double()
correct = correct.sum()
return correct / len(labels)
2、self-attention自注意力层的实现
密集型矩阵自注意力层的实现
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
class GraphAttentionLayer(nn.Module):
"""
Simple GAT layer, similar to https://arxiv.org/abs/1710.10903
"""
def __init__(self, in_features, out_features, dropout, alpha, concat=True):
super(GraphAttentionLayer, self).__init__()
self.dropout = dropout
self.in_features = in_features
self.out_features = out_features
self.alpha = alpha
self.concat = concat
self.W = nn.Parameter(torch.zeros(size=(in_features, out_features)))
nn.init.xavier_uniform_(self.W.data, gain=1.414)
self.a = nn.Parameter(torch.zeros(size=(2*out_features, 1)))
nn.init.xavier_uniform_(self.a.data, gain=1.414)
self.leakyrelu = nn.LeakyReLU(self.alpha)
def forward(self, input, adj):
h = torch.mm(input, self.W)
N = h.size()[0]
a_input = torch.cat([h.repeat(1, N).view(N * N, -1), h.repeat(N, 1)], dim=1).view(N, -1, 2 * self.out_features)
e = self.leakyrelu(torch.matmul(a_input, self.a).squeeze(2))
zero_vec = -9e15*torch.ones_like(e)
attention = torch.where(adj > 0, e, zero_vec)
attention = F.softmax(attention, dim=1)
attention = F.dropout(attention, self.dropout, training=self.training)
h_prime = torch.matmul(attention, h)
if self.concat:
return F.elu(h_prime) # 不是最后一层
else:
return h_prime # 最后一层
def __repr__(self):
return self.__class__.__name__ + ' (' + str(self.in_features) + ' -> ' + str(self.out_features) + ')'
forward中完成了论文中公式:
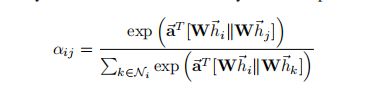
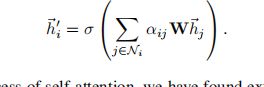
通过该attention layer,就完成了从论文中输入特征 h = { h 1 , h 2 , . . . . h N } h=\left \{ h_{1},h_{2},....h_{N}\right \} h={h1,h2,....hN}
到输出状态 h ′ = { h 1 , h 2 , . . . . h N } h^{'}=\left \{ h_{1},h_{2},....h_{N}\right \} h′={h1,h2,....hN}的转变。
优化的参数是注意力系数a和权重矩阵a。
注意力系数a在边未连接时取负无穷,在边连接的情况下不断优化a的值,使得注意更重要的连接边。
稀疏矩阵的layer层
# 自定义后向传播
class SpecialSpmmFunction(torch.autograd.Function):
"""Special function for only sparse region backpropataion layer."""
@staticmethod
def forward(ctx, indices, values, shape, b):
assert indices.requires_grad == False
a = torch.sparse_coo_tensor(indices, values, shape)
ctx.save_for_backward(a, b)
ctx.N = shape[0]
return torch.matmul(a, b)
@staticmethod
def backward(ctx, grad_output):
a, b = ctx.saved_tensors
grad_values = grad_b = None
if ctx.needs_input_grad[1]:
grad_a_dense = grad_output.matmul(b.t())
edge_idx = a._indices()[0, :] * ctx.N + a._indices()[1, :]
grad_values = grad_a_dense.view(-1)[edge_idx]
if ctx.needs_input_grad[3]:
grad_b = a.t().matmul(grad_output)
return None, grad_values, None, grad_b
# 自定义后向传播的模型
class SpecialSpmm(nn.Module):
def forward(self, indices, values, shape, b):
return SpecialSpmmFunction.apply(indices, values, shape, b)
# 与密集型表示基本相同
class SpGraphAttentionLayer(nn.Module):
"""
Sparse version GAT layer, similar to https://arxiv.org/abs/1710.10903
"""
def __init__(self, in_features, out_features, dropout, alpha, concat=True):
super(SpGraphAttentionLayer, self).__init__()
self.in_features = in_features
self.out_features = out_features
self.alpha = alpha
self.concat = concat
self.W = nn.Parameter(torch.zeros(size=(in_features, out_features)))
nn.init.xavier_normal_(self.W.data, gain=1.414)
self.a = nn.Parameter(torch.zeros(size=(1, 2*out_features)))
nn.init.xavier_normal_(self.a.data, gain=1.414)
self.dropout = nn.Dropout(dropout)
self.leakyrelu = nn.LeakyReLU(self.alpha)
self.special_spmm = SpecialSpmm()
def forward(self, input, adj):
dv = 'cuda' if input.is_cuda else 'cpu'
N = input.size()[0]
edge = adj.nonzero().t() # 返回边的非零索引
h = torch.mm(input, self.W)
# h: N x out
assert not torch.isnan(h).any()
# Self-attention on the nodes - Shared attention mechanism
edge_h = torch.cat((h[edge[0, :], :], h[edge[1, :], :]), dim=1).t()
# edge: 2*D x E
edge_e = torch.exp(-self.leakyrelu(self.a.mm(edge_h).squeeze()))
assert not torch.isnan(edge_e).any()
# edge_e: E
e_rowsum = self.special_spmm(edge, edge_e, torch.Size([N, N]), torch.ones(size=(N,1), device=dv))
# e_rowsum: N x 1
edge_e = self.dropout(edge_e)
# edge_e: E
h_prime = self.special_spmm(edge, edge_e, torch.Size([N, N]), h)
assert not torch.isnan(h_prime).any()
# h_prime: N x out
h_prime = h_prime.div(e_rowsum) # .div(),除法,元素相除
# h_prime: N x out
assert not torch.isnan(h_prime).any()
if self.concat:
# if this layer is not last layer,
return F.elu(h_prime)
else:
# if this layer is last layer,
return h_prime
def __repr__(self):
return self.__class__.__name__ + ' (' + str(self.in_features) + ' -> ' + str(self.out_features) + ')'
稀疏layer只是为了能加快GAT的求解,当batch_size=1时使用。
但是该layer模块只是定义了一层的attention机制。感觉cora数据集更加合适系数版本的注意力层。
稀疏版本的运行速度是非稀疏版本的10倍以上。
多头attention
import torch
import torch.nn as nn
import torch.nn.functional as F
from layers import GraphAttentionLayer, SpGraphAttentionLayer
class GAT(nn.Module):
def __init__(self, nfeat, nhid, nclass, dropout, alpha, nheads):
"""Dense version of GAT."""
super(GAT, self).__init__()
self.dropout = dropout
self.attentions = [GraphAttentionLayer(nfeat, nhid, dropout=dropout, alpha=alpha, concat=True) for _ in range(nheads)]
for i, attention in enumerate(self.attentions):
self.add_module('attention_{}'.format(i), attention)
self.out_att = GraphAttentionLayer(nhid * nheads, nclass, dropout=dropout, alpha=alpha, concat=False)
def forward(self, x, adj):
x = F.dropout(x, self.dropout, training=self.training)
x = torch.cat([att(x, adj) for att in self.attentions], dim=1)
x = F.dropout(x, self.dropout, training=self.training)
x = F.elu(self.out_att(x, adj))
return F.log_softmax(x, dim=1)
class SpGAT(nn.Module):
def __init__(self, nfeat, nhid, nclass, dropout, alpha, nheads):
"""Sparse version of GAT.
An experimental sparse version is also available,
working only when the batch size is equal to 1"""
super(SpGAT, self).__init__()
self.dropout = dropout
self.attentions = [SpGraphAttentionLayer(nfeat,
nhid,
dropout=dropout,
alpha=alpha,
concat=True) for _ in range(nheads)]
for i, attention in enumerate(self.attentions):
self.add_module('attention_{}'.format(i), attention)
self.out_att = SpGraphAttentionLayer(nhid * nheads,
nclass,
dropout=dropout,
alpha=alpha,
concat=False)
def forward(self, x, adj):
x = F.dropout(x, self.dropout, training=self.training)
x = torch.cat([att(x, adj) for att in self.attentions], dim=1)
x = F.elu(x)
x = F.dropout(x, self.dropout, training=self.training)
x = self.out_att(x, adj)
return F.log_softmax(x, dim=1)
该模块实现了两层的GAT,第一层GAT通过拼接实现:K=8。
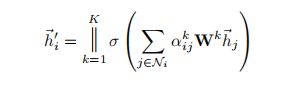
在第一层结束后加上非线性激活函数elu
第二层GAT实现输出:使用平均函数,但实验表明,多头机制无任何帮助,所以取K=1,单层注意力机制输出。
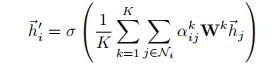
在该模型上的最后实验结果在测试集达到了85%,比论文中高出1.7个百分点。
GCN和GAT的对比
2017年GCN出现后引起了很大反响,它的基本思想就是把一个节点在图中的高维度邻接信息降维到一个低维的向量表示。
GCN的优点:可以捕捉graph的全局信息,从而很好的表示node的特征
GCN的缺点:1、需要把所有的节点都参与训练才能得到node,这就使得会带来极大的开销,限制了GCN在大的网络中实现。
2、对于一个图结构训练好的模型,不能运用于另一个图结构。
GAT的优点:1、注意力机制共享了图中所有的边,因此他不需要提前访问图中所有的图结构以及所有节点。
2、可以处理任意大小输入的问题,并且关注最具有影响能力的输入。在cora数据集中训练的参数可以直接应用到Citeseer上。