人工智能中的搜索

最近在mooc学习人工智能：模型于算法，下面记录课上的例子和学到的东西。

首先，人工智能搜索是从海量的信息源中通过约束条件和额外信息运用算法找到问题所对应的答案。

 

正所谓，你见，或者不见我，我就在那里不悲不喜     ----扎西拉姆多多

以寻找最短路径问题为例：

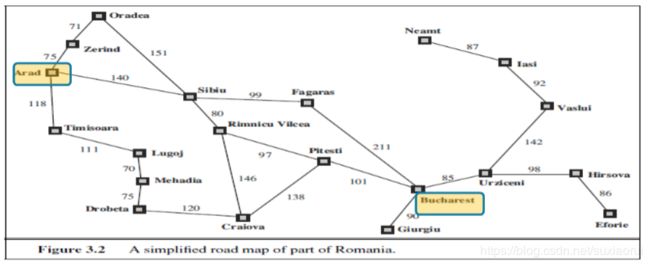
问题：寻找从Arad到Bucharest的一条最短路径

下面简单说说搜索算法的形式化描述：（状态、动作、状态转移、路径、测试目标）

状态：从原问题转化出的问题描述中。例如，在最短路径问题中，城市可作为状态。将原问题对应的状态称为初始状态。

动作：从当前所处的状态转移到下一时刻的状态所进行的操作。一般而言这些操作都是离散的。

状态转移：对某一时刻对应状态进行某一操作后，所能达到的状态。

路径：一个状态序列。将状态序列被一系列操作所连接。如从Arad到Bucharest所形成的路径。

目标测试：评估当前状态是否为所解的目标状态。

 

启发式搜索又称有信息搜索，在搜索的过程中liyong利用与所求解问题相关的辅助信息，其代表算法为贪婪最佳优先搜索（Greedy best-first search）和搜索。

 

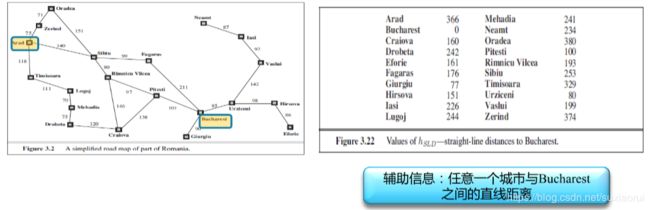
辅助信息：所求解问题之外、与所求解问题相关的特定信息或知识。如该例子中辅助信息为任意一个城市与Bucharest之间的直线距离。

评价函数（evaluation function）f(n)：从当前节点n出发，根据评价函数来选择后续节点。

启发函数（heuristic function）h(n)：计算从节点n到目标节点之间所形成路径的最小代价值。这里将两点之间的直线距离作为启发函数。

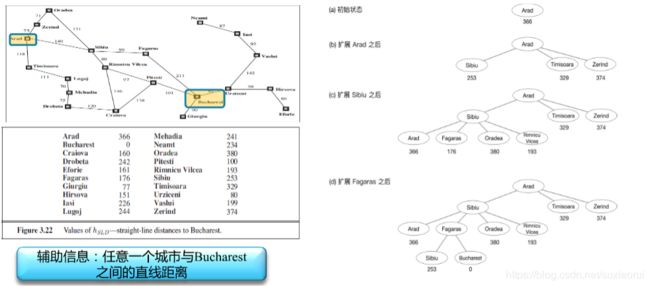
下面用贪婪最佳优先搜索：评价函数f(n)=启发函数h(n)

 

可以得到路线：Arad→Sibiu→Fagaras→Bucharest，但是这并不是最短路线。

不足之处：1.从上可见贪婪最佳优先搜索不是最优的。上述路线比Arad→Sibiu→Rimnicu Vilcea→Bucharest的路径长32公里。

                  2.启发函数代价最小化这一目标 会对错误的起点比较敏感，考虑从Iasi到Fagaras的问题，由启发式建议须先扩展到

Neamt，因为其离Fagaras最近，但是这是一条存在死循环的路径。

                  3.贪婪优先算法也是不完备的。所谓不完备即它可能沿着一条无限的路劲走下去而不回来做其他的选择尝试，因此无法找到最佳路径这一答案。

                 4.在最坏的情况下，贪婪最佳优先搜索的时间复杂度和空间复杂度都是O()，其中是节点的分支因子数目、是搜索空间的最大深度。

因此，需要设计一个良好的启发函数。接着介绍一下搜索。

           定义评价函数：

           表示从起始节点到节点n的开销代价值，表示从节点n到目标节点路径中所估算的最小开小代价值。

           可视为经过节点n、具有最小开销代价值的路径。

也可以说 是评估函数，是当前最小开销代价，是后续最小开销代价。

为了保证算法是最优，需要启发函数是可容的和一致的(或者也称是单调的)。

最优：不存在另外一个解法能得到比算法所求得解法具有更小开销代价。

可容：专门针对启发函数而言，即启发函数不会过高估计从节点n到目标节点之间的实际开销代价(即小于等于实际开销)。如可将两点之间的直线距离作为启发函数，从而保证其可容。

一致性(单调性)：假设节点n的后续节点是n',则从n 到目标节点之间的开销代价一定小于从n到n'的开销再加上从n'到目标节点之间的开销，即。这里n'是n经过a所抵达的后续节点，指n'和n之间的开销代价。

 

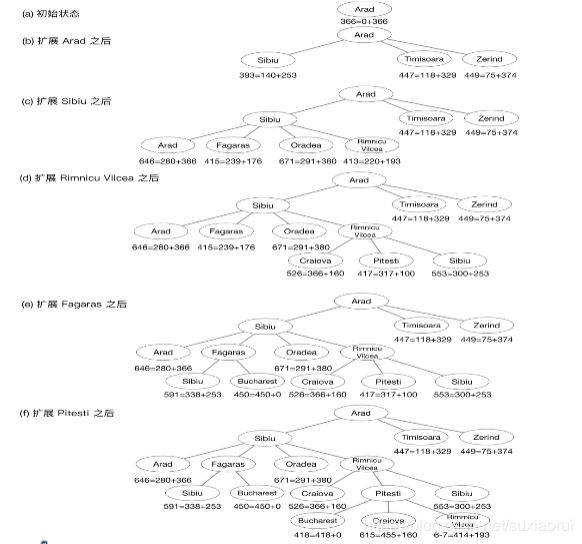
可见A*算法得出的路径即是最短路径，是最优结果。

1.A*算法保持最优的条件：启发函数具有可容性和一致性。

2.将直线距离作为启发函数h(n)，则启发函数一定是可容的，因为其不会高估开销代价。

3.g(n)是从起点节点到节点n的实际开销代价，且，因此f(n)不会高估经过节点n路径的实际开销。