基于遗传算法的传统作业车间调度问题的求解(Job-shop scheduling problem based on genetic algorithm)
1、前言
最近学习了一下传统作业车间调度问题的理论与算法并使用遗传算法和作业车间实例,亲自编写matlab程序实现了一下,体验了遗传算法物竞天择的奇妙之处。趁刚写完算法的热度还在,给大家分享一下,有问题欢迎评论留言,共同探讨学习,完整代码见基于遗传算法的JSP问题求解 或者 JSP_GA。
2、车间调度问题的描述
n 个不同的工件在 m 台机器上加工,其要满足工序约束 ,即每个工件包含了一道或者是多道工序 ,并且同一个工件所经过的工序有先后的顺序 ,每道工序可以在一台或者多台(这里考虑传统的车间作业,即每道工序在一台机器上加工)机器上进行加工,每个工序的加工时间由加工的机器给定。所需满足的约束条件如下:
1、同一时刻、同一机器只能加工一道工序 ;
2、一道工序同一时刻只能在一台机器上加工,且不能中途中断 ;
3、同一工件的工序先后顺序有约束 ,而不同工件加工工序之间没有先后顺序的约束;
4、不同工件之间优先级是相同的;
5、不考虑机器故障等随机性因素。
调度的目标就是确定每个机器上工序的加工顺序和每个工序的开工时间,使得最大完工时间 C m a x C_{max} Cmax (makspan)最小或者其他指标达到最优。
3 用遗传算法求解车间调度问题
3.1、编码与解码
采用基于工序的编码方式。每个染色体用一个包含n×m个代表工序的基因序列,是一个所有工序的一个排列。其特点是任意基因串的排列均能表示可行的调度。对于一个n个工件在m台机器加工的调度问题,其染色体由n×m个基因组成,每个工件序号只能在染色体中出现m次,从左到右扫描染色体,对于第k次出现的工件序号,表示该工件的第k道工序。
| 工件 | 工序1(机器号/加工时间) | 工序2(机器号/加工时间) | 工序3(机器号/加工时间) |
|---|---|---|---|
| J 1 J_1 J1 | 1(3) | 2(2) | 3(3) |
| J 2 J_2 J2 | 3(2) | 1(3) | 2(4) |
| J 3 J_3 J3 | 2(2) | 3(2) | 1(3) |
例如一个3x3的JSP问题,如上表所示,它的一条染色体为[2 1 1 3 1 2 3 3 2],其中1表示工件 J 1 J_1 J1,2表示工件 J 2 J_2 J2,3表示工件 J 3 J_3 J3。染色体中的3个1表示工件 J 1 J_1 J1的三个工序,此染色体对应的机器分配为[3 1 2 2 3 1 3 1 2],每台机器上工件加工顺序如下表。
| 机器号 | 工件顺序 | ||
|---|---|---|---|
| m 1 m_1 m1 | 1(3) | 2(2) | 3(3) |
| m 2 m_2 m2 | 3(2) | 1(3) | 2(4) |
| m 3 m_3 m3 | 2(2) | 3(2) | 1(3) |
解码过程和编码过程相反,解码分为一般解码或者称为半主动解码、主动解码和全主动解码。本文使用半主动解码方式进行染色体解码。
对应的Matlab代码如下:
1)编码
%% Coding
%Coding is based on the step of the job
initial=[];
for i = 1:num_of_jobs
for j = 1:number_of_machines
initial=[initial i];
end
end
%Generate population with chromosome containing random genes
for i = 1:PopSize
population(i,:)=initial(randperm(length(initial(:))));
end
2)解码
function [Jobs,Cmax,MachineList,ST,PT] = SemiActiveDecoding(T,Chromosome)
%% INPUT:
%T--input matrix:
%Each instance consists of a line of description, a line containing the number of jobs and the number of machines, and then one line for each job,
%listing the machine number and processing time for each step of the job. The machines are numbered starting with 0.
% +++++++++++++++++++++++++++++
% Fisher and Thompson 6x6 instance, alternate name (mt06)
% 6 6
% 2 1 0 3 1 6 3 7 5 3 4 6
% 1 8 2 5 4 10 5 10 0 10 3 4
% 2 5 3 4 5 8 0 9 1 1 4 7
% 1 5 0 5 2 5 3 3 4 8 5 9
% 2 9 1 3 4 5 5 4 0 3 3 1
% 1 3 3 3 5 9 0 10 4 4 2 1
% +++++++++++++++++++++++++++++
%Chromosome -- A chromosome to be decoded
%% OUTPUT:
%JobList-- job sequences
%Cmax --the max makespan
%MachineList--The machine sequences corresponding to chromosome
%ST --the start time for each job step in chromosome
%PT --The operation time for each job step in chromome
%% start
[num_of_jobs,number_of_machines]=size(T);
number_of_machines = number_of_machines/2; % number of jobs and machines
Jobs = unique(Chromosome);
StepList = []; %steps for all genes
MachineList = [];
DecodedGenes =[];
ST = [];
PT = [];
len_of_chromosome = num_of_jobs*number_of_machines;
%% Caculate MachineList and PT
for index = 1:len_of_chromosome
DecodedGenes=[DecodedGenes Chromosome(index)];
postion = length(find(DecodedGenes==Chromosome(index)));
StepList = [StepList postion];
pos1 = postion*2-1;
pos2 =postion*2;
MachineList = [MachineList T(Chromosome(index),pos1)];
PT = [PT T(Chromosome(index),pos2)];
end
%% Caculate ST
Machines = unique(MachineList);
steps = unique(StepList);
job_start_time = cell(num_of_jobs,1);
job_end_time = cell(num_of_jobs,1);
machine_start_time = cell(number_of_machines,1);
machine_end_time = cell(number_of_machines,1);
machine_state = zeros(1,number_of_machines); %0--FirstWork;1--NotFirst
for index = 1:len_of_chromosome
job = Chromosome(index);
machine = MachineList(index);
pt = PT(index);
step = StepList(index);
pos_m = find(Machines==machine);
pos_j = find(Jobs==job);
if step==1 %first step without considering the constrains between steps of same job
if machine_state(pos_m)==0 % The machine is first used
job_start_time{pos_j}=[0,pos_m];
job_end_time{pos_j}=[job_start_time{pos_j}(1)+pt,pos_m];
else
job_start_time{pos_j}=[machine_end_time{pos_m}(1),pos_m];
job_end_time{pos_j}=[job_start_time{pos_j}(1)+pt,pos_m];
end
else
if machine_state(pos_m)==0 % The machine is first used
job_start_time{pos_j}=[job_end_time{pos_j}(1),pos_m];
job_end_time{pos_j}=[job_start_time{pos_j}(1)+pt,pos_m];
else
job_start_time{pos_j}=[max(machine_end_time{pos_m}(1),job_end_time{pos_j}(1)),pos_m];
job_end_time{pos_j}=[job_start_time{pos_j}(1)+pt,pos_m];
end
end
machine_start_time{pos_m}= [job_start_time{pos_j}(1)];
machine_end_time{pos_m} = [job_end_time{pos_j}(1)];
machine_state(pos_m)=1;
ST=[ST, job_start_time{pos_j}(1)];
end
%% Caculate Cmax
end_time=cell2mat(job_end_time);
Cmax = max(end_time(:,1));
end
3.2 选择操作
在遗传算法中,适应度是个体对生存环境的适应程度,适应度高的个体将获得更多的生存机会。选择算子根据适应度的值选择个体遗传到下一代群体中。本文采用 C m a x C_{max} Cmax作为适应度函数,并使用赌盘轮方法选择,每个个体生存概率为:
P n = f n / ∑ i = 1 n f i P_n = f_n/\sum_{i=1}^{n}f_i Pn=fn/∑i=1nfi
对应源码为:
%% Selection using Roulette Wheel
Parent = [];
TotalFitness=sum(Pfit_value); % Calculate the total fitness value - the denominator used in roulette
for i=1:PopSize % Calculate the probability of each individual being selected,
Pfit_value(i)=Pfit_value(i)/TotalFitness; % the molecule used in roulette
end
% select (PopSize-1)/2
SelectedChromosome=zeros(1,len_of_chromosome);
for memeber=1:(PopSize-1)/2
WheelSelectionNumber=rand;
Toltal = 0;
for i=1:PopSize
Toltal=Toltal+Pfit_value(i);
if (Toltal-Pfit_value(i))< WheelSelectionNumber && Toltal>=WheelSelectionNumber
for gene = 1:len_of_chromosome
SelectedChromosome(gene)=population(i,gene); % select one chromosome
end
break
else
for gene = 1:len_of_chromosome
SelectedChromosome(gene)=population(i,gene); % select current chromosome
end
end
end
for gene = 1:len_of_chromosome
Parent(memeber,gene)=SelectedChromosome(gene);
end
end
3.3、基于工序编码的交叉算子POX
交叉是遗传算法的最重要操作,决定遗传算法的全局搜索能力。遗传算法假定,若一个个体的适应度较好,那么基因链码中的某些相邻关系片段是好的,并且由这些链码所构成的其他个体的适应度也较好。在JSP问题中设计交叉算子最重要的标准是子代对父代优良特征的继承性和子代的可行性。相对于JOX、SXX、SPX、PPX等交叉算子,基于工序编码的交叉算子POX(precedence operation crossover),它能够很好地继承父代优良特征并且子
代总是可行的。设父代 mxn 染色体Parent1和Parent2,POX产生Children1和Children2, POX交叉的具体流程如下:
- 随机划分工件集{1,2,3,…,n}为两个非空的子集 J 1 J_1 J1和 J 2 J_2 J2;
- 复制Parent1包含在J1的工件到Children1,Parent2包含在J1的工件到Children2,保留它们的位置;
- 复制Parent2包含在J2的工件到Children1,Parent1包含在J2的工件到Children2,保留它们的顺序。
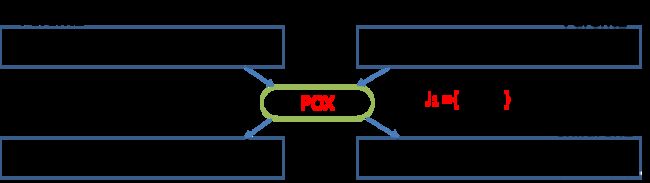
图1 POX交叉算子
图1说明了4× 3调度问题的两个父代交叉过程。两父代Parent1、Parent2交叉生成Children1染色体基因为[3 2 2 1 2 3 1 4 4 1 4 3],Children2染色体基因为[4 1 3 4 2 2 1 1 2 4 3 3]。可以看出经过POX交叉保留了工件{2,3}在机器上的位置,使子代继承父代每台机器上工件次序。不同于JOX交叉,由于POX交叉是基于工序编码,生成子代染色体无须运用GT方法将不可行调度强制转化为可行调度。
对应的Matlab源码如下:
Children_group1=[];
for i=1:(PopSize-1)/2
%Parent individuals are selected for crossover operation:
%Parent1 is selected sequentially and Parent2 is selected randomly.
index_parent2 = randi([1,(PopSize-1)/2]);
for gene = 1:len_of_chromosome
Parent1(gene)=Parent(i,gene);
%Parent2(gene)=BestChromosome(gene);%Cross with best chromosome
Parent2(gene)=Parent(index_parent2,gene);
end
Children1=zeros(1,len_of_chromosome);
Children2=zeros(1,len_of_chromosome);
if rand(1)<=Pc %The probability is used to determine whether crossover operations are required
%Randomly divide the set of jobs {1,2,3...,n} into two non-empty sub-sets J1 and J2.
num_J1 = randi([1,num_of_jobs]);
if num_J1==num_of_jobs
num_J1 = fix(num_of_jobs/2);
end
J = randperm(num_of_jobs);
J1 =J(1:num_J1);
% J2 =J(num_J1+1:n);
%Copy the jobs that Parent1 contains in J1 to Children1,
%and Parent2 contains in J1 to Children2, and keep them in place.
for index = 1:num_J1
%Look for the jobs that Parent1 and Parent2 contain in J1
job = J1(index);
for j = 1:len_of_chromosome
if job == Parent1(j)
Children1(j)=Parent1(j);
Parent1(j)=0;
end
if job == Parent2(j)
Children2(j)=Parent2(j);
Parent2(j)=0;
end
end
end
%Copy the jobs that Parent1 contains in J2 to Children2,
%and Parent2 contains in J2 to Children1 in their order.
for index=1:len_of_chromosome
if Parent1(index)~=0
for j=1:len_of_chromosome
if Children2(j)==0
Children2(j)=Parent1(index);
break;
end
end
end
if Parent2(index)~=0
for j=1:len_of_chromosome
if Children1(j)==0
Children1(j)=Parent2(index);
break;
end
end
end
end %POX Cross over
else
Children1 = Parent1;
Children2 = Parent2;
end
% condtion = rand(1);
for gene = 1:len_of_chromosome
% if condtion>0.5
% Children_group1(i, gene)=Children1(gene);
% else
% Children_group1(i, gene)=Children2(gene);
% end
Children_group1(2*i-1, gene)=Children1(gene);
Children_group1(2*i, gene)=Children2(gene);
end
end
3.4、变异
在传统遗传算法中,变异是为了保持群体的多样性,它由染色体较小的扰动产生。这里的变异操作,是针对单个染色体的不同基因序号进行交换。过程比较简单,无须赘述。
源码如下:
%% Mutation
Children_group2=[];
for i=1:(PopSize-1)
for gene = 1:len_of_chromosome
temp(gene)=Children_group1(i,gene);
end
if rand(1)<Pm
for j=1:4
pos1=randi([1,len_of_chromosome]); % Choose the sequence number of a gene to be mutated
pos2=randi([1,len_of_chromosome]); % Choose the another sequence number of a gene to be mutated
Gene=temp(pos1);
temp(pos1)=temp(pos2);
temp(pos2)=Gene;
end
end
for gene = 1:len_of_chromosome
Children_group2(i,gene)=temp(gene);
end
end
3.5、绘制甘特图
这部分就是将最优的染色体绘制出来,直接上代码吧:
%% GanntGraf
function GanntGraf(job_array,XX,YY,ST,PT,fit,TITLE)
%job_array--jobs list,
%XX---one chromosome,
%YY-----Decoded machine sequence,
%ST-----Start time of corresponding steps,
%PT-----Operation time of corresponding steps,
%fit----fitness
num_j=numel(job_array);
num_m=numel(unique(YY));
num_op=numel(XX); %the number of all steps
fit_n=floor(log10(fit))+1; %Determine the upper bound on the X-axis of the gantt chart according to the fit value
fit_str=num2str(fit);
if numel(fit_str)>1
if str2double(fit_str(2))>=5
maxX=(10^(fit_n-1))*(str2double(fit_str(1))+1);
elseif str2double(fit_str(2))<5
maxX=(10^(fit_n-1))*(str2double(fit_str(1)))+(10^(fit_n-2)*5);
end
elseif numel(fit_str)==1
maxX=(10^(fit_n-1))*(str2double(fit_str(1))+1);
end
figure(2);
axis([0,maxX,0,num_m+0.5]); % x and y
set(gca,'xtick',0:maxX/10:maxX) ; %The increase step in the X-axis
set(gca,'ytick',0:1:num_m+0.5) ; %The increase step in the X-axis
xlabel('Processing Time','FontWeight','Bold','FontSize',15),ylabel('Machine Number','FontWeight','Bold','FontSize',15);%x轴 y轴的名称
color=[
0.9503 0.1669 0.4071
0.0077 0.9092 0.5791
0.4863 0.7758 0.4187
0.8415 0.0616 0.8317
0.6903 0.7108 0.3491
0.7798 0.5519 0.8137
0.5925 0.4321 0.9752
0.6505 0.1452 0.2776
0.7458 0.2480 0.8866
0.5382 0.2022 0.5197
0.4124 0.0269 0.5633
0.9119 0.3039 0.0125
0.9423 0.0790 0.2112
0.4246 0.3765 0.3313
0.9489 0.6026 0.1701
0.9225 0.8885 0.0108
0.5905 0.5817 0.5152
0.9253 0.0745 0.3962
0.9503 0.1669 0.4071
0.0077 0.9092 0.5791
0.4863 0.7758 0.4187
0.8415 0.0616 0.8317
0.6903 0.7108 0.3491
0.7798 0.5519 0.8137
0.5925 0.4321 0.9752
0.6505 0.1452 0.2776];
n_color=zeros(num_op,3);
for i=1:num_j
counter_j(i)=1; %Record the steps of each job
end
for i=1:length(XX)
n_color(i,:)=color(XX(i),:);
end
rec=[0,0,0,0]; %temp data space for every rectangle
for i = 1:num_op
job=XX(i);
pos_j=find(job_array==job);
rec(1) = ST(i);
rec(2) = YY(i)-0.3;
rec(3) = PT(i);
rec(4) = 0.4;
txt=sprintf('%d-%d',job,counter_j(pos_j(1)));
rectangle('Position',rec,'LineWidth',0.5,'LineStyle','-','faceColor',n_color(i,:));%draw every rectangle
text(ST(i)+0.4,(YY(i))-0.1,txt,'FontWeight','Bold','FontSize',15); %label the id of every task
counter_j(pos_j(1))=counter_j(pos_j(1))+1;
end
title(TITLE,'FontWeight','Bold','FontSize',15);
hold on;
grid on;
plot([fit,fit],[0,num_m+0.5],'r','linewidth',2);
text(fit,0.5,['Cmax=',num2str(fit)],'FontWeight','Bold','FontSize',15);
end
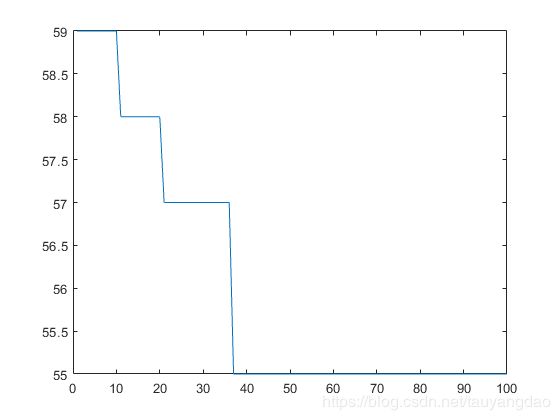
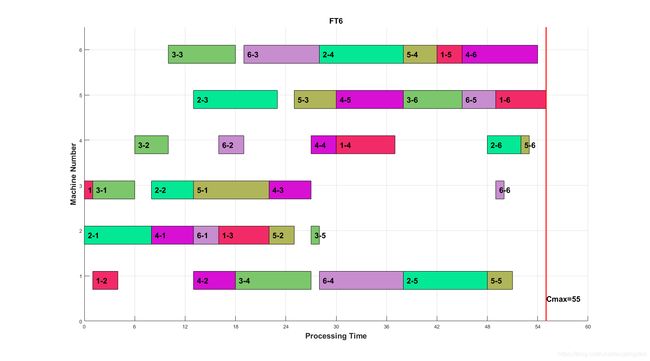
3.6、实验验证
使用上述的代码,验证了FT6基准实例。
代码:
clear;
clc;
FT6 = [
2 1 0 3 1 6 3 7 5 3 4 6
1 8 2 5 4 10 5 10 0 10 3 4
2 5 3 4 5 8 0 9 1 1 4 7
1 5 0 5 2 5 3 3 4 8 5 9
2 9 1 3 4 5 5 4 0 3 3 1
1 3 3 3 5 9 0 10 4 4 2 1 ];
FT10 =[
0 29 1 78 2 9 3 36 4 49 5 11 6 62 7 56 8 44 9 21
0 43 2 90 4 75 9 11 3 69 1 28 6 46 5 46 7 72 8 30
1 91 0 85 3 39 2 74 8 90 5 10 7 12 6 89 9 45 4 33
1 81 2 95 0 71 4 99 6 9 8 52 7 85 3 98 9 22 5 43
2 14 0 6 1 22 5 61 3 26 4 69 8 21 7 49 9 72 6 53
2 84 1 2 5 52 3 95 8 48 9 72 0 47 6 65 4 6 7 25
1 46 0 37 3 61 2 13 6 32 5 21 9 32 8 89 7 30 4 55
2 31 0 86 1 46 5 74 4 32 6 88 8 19 9 48 7 36 3 79
0 76 1 69 3 76 5 51 2 85 9 11 6 40 7 89 4 26 8 74
1 85 0 13 2 61 6 7 8 64 9 76 5 47 3 52 4 90 7 45];
FT20 = [
0 29 1 9 2 49 3 62 4 44
0 43 1 75 3 69 2 46 4 72
1 91 0 39 2 90 4 12 3 45
1 81 0 71 4 9 2 85 3 22
2 14 1 22 0 26 3 21 4 72
2 84 1 52 4 48 0 47 3 6
1 46 0 61 2 32 3 32 4 30
2 31 1 46 0 32 3 19 4 36
0 76 3 76 2 85 1 40 4 26
1 85 2 61 0 64 3 47 4 90
1 78 3 36 0 11 4 56 2 21
2 90 0 11 1 28 3 46 4 30
0 85 2 74 1 10 3 89 4 33
2 95 0 99 1 52 3 98 4 43
0 6 1 61 4 69 2 49 3 53
1 2 0 95 3 72 4 65 2 29
0 37 2 13 1 21 3 89 4 55
0 86 1 74 4 88 2 48 3 79
1 69 2 51 0 11 3 89 4 74
0 13 1 7 2 76 3 52 4 45 ];
Iterations =100;
PopSize = 500;
Pc = 0.9;
Pm = 0.05;
[Chromosome] = POX_GA(FT6,Iterations,PopSize,Pc,Pm); % get the best chromosome
[Jobs,Cmax,MachineList,ST,PT] = SemiActiveDecoding(FT6,Chromosome); % decoding the best chromosome
MachineList=MachineList+1; % Change the machine number from 0 to 1
GanntGraf(Jobs,Chromosome,MachineList,ST,PT,Cmax,"FT6") ; %draw GanntGtaf
4 小结
使用遗传算法解决传统的作业车间调度,已经是比较成熟的解决方法了。但是,遗传算法存在的早熟导致局部最优问题依然没有找到完美的解决方法。如何在种群进化早期保证种群多样性是需要解决的问题,另外研究柔性车间作业调度,对于当前柔性制造系统的意义比较大,也是下一步重点关注的领域。以上内容是个人总结,不喜勿喷,有问题欢迎批评指正!