matplotlib基础教程-3D绘图（2）

基本3D图的绘制

Matplotlib 已经内置了三维图形，所以我们只需要引入这些完整的模块就可以了：

from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt

使用axes3d是因为它需要不同种类的轴域，以便在三维中实际绘制一些东西。 下面：

fig = plt.figure()
ax1 = fig.add_subplot(111, projection='3d')

在这里，我们像通常一样定义图形，然后我们将ax1定义为通常的子图，只是这次使用 3D 投影。 我们需要这样做，以便提醒 Matplotlib 我们要提供三维数据。

现在让我们创建一些 3D 数据：

x = [1,2,3,4,5,6,7,8,9,10]
y = [5,6,7,8,2,5,6,3,7,2]
z = [1,2,6,3,2,7,3,3,7,2]

接下来，我们绘制它。 首先，让我们展示一个简单的线框示例：

ax1.plot_wireframe(x,y,z)

最后：

ax1.set_xlabel('x axis')
ax1.set_ylabel('y axis')
ax1.set_zlabel('z axis')

plt.show()

我们完整的代码是：

from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
from matplotlib import style

style.use('fivethirtyeight')

fig = plt.figure()
ax1 = fig.add_subplot(111, projection='3d')

x = [1,2,3,4,5,6,7,8,9,10]
y = [5,6,7,8,2,5,6,3,7,2]
z = [1,2,6,3,2,7,3,3,7,2]

ax1.plot_wireframe(x,y,z)

ax1.set_xlabel('x axis')
ax1.set_ylabel('y axis')
ax1.set_zlabel('z axis')

plt.show()

结果为（包括所用的样式）：

这些 3D 图形可以进行交互。 首先，您可以使用鼠标左键单击并拖动来移动图形。 您还可以使用鼠标右键单击并拖动来放大或缩小。

3D 散点图的绘制

绘制 3D 散点图非常类似于通常的散点图以及 3D 线框图。

一个简单示例：

from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
from matplotlib import style

style.use('ggplot')

fig = plt.figure()
ax1 = fig.add_subplot(111, projection='3d')

x = [1,2,3,4,5,6,7,8,9,10]
y = [5,6,7,8,2,5,6,3,7,2]
z = [1,2,6,3,2,7,3,3,7,2]

x2 = [-1,-2,-3,-4,-5,-6,-7,-8,-9,-10]
y2 = [-5,-6,-7,-8,-2,-5,-6,-3,-7,-2]
z2 = [1,2,6,3,2,7,3,3,7,2]

ax1.scatter(x, y, z, c='g', marker='o')
ax1.scatter(x2, y2, z2, c ='r', marker='o')

ax1.set_xlabel('x axis')
ax1.set_ylabel('y axis')
ax1.set_zlabel('z axis')

plt.show()

结果为：

要记住你可以修改这些绘图的大小和标记，就像通常的散点图那样。

3D 条形图的绘制

在这个 Matplotlib 教程中，我们要介绍 3D 条形图。 3D 条形图是非常独特的，因为它允许我们绘制多于 3 个维度。 不，你不能超过第三个维度来绘制，但你可以绘制多于 3 个维度。

对于条形图，你需要拥有条形的起点，条形的高度和宽度。 但对于 3D 条形图，你还有另一个选项，就是条形的深度。 大多数情况下，条形图从轴上的条形平面开始，但是你也可以通过打破此约束来添加另一个维度。 然而，我们会让它非常简单：

from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import style
style.use('ggplot')

fig = plt.figure()
ax1 = fig.add_subplot(111, projection='3d')

x3 = [1,2,3,4,5,6,7,8,9,10]
y3 = [5,6,7,8,2,5,6,3,7,2]
z3 = np.zeros(10)

dx = np.ones(10)
dy = np.ones(10)
dz = [1,2,3,4,5,6,7,8,9,10]

ax1.bar3d(x3, y3, z3, dx, dy, dz)


ax1.set_xlabel('x axis')
ax1.set_ylabel('y axis')
ax1.set_zlabel('z axis')

plt.show()

注意这里，我们必须定义x、y和z，然后是 3 个维度的宽度、高度和深度。 这会生成：

总结

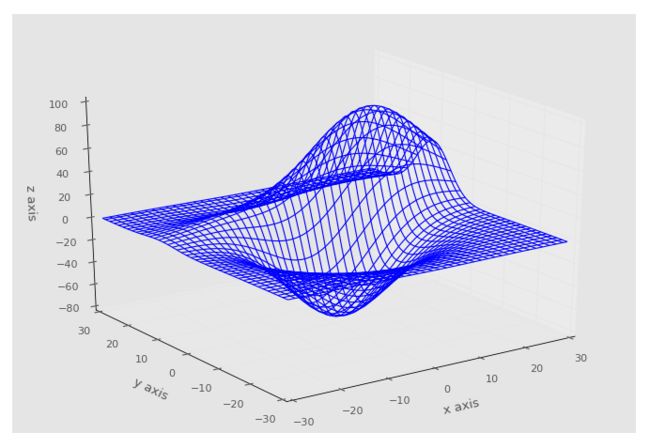
欢迎阅读最后的 Matplotlib 教程。 在这里我们将整理整个系列，并显示一个稍微更复杂的 3D 线框图：

from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import style
style.use('ggplot')

fig = plt.figure()
ax1 = fig.add_subplot(111, projection='3d')

x, y, z = axes3d.get_test_data()

print(axes3d.__file__)
ax1.plot_wireframe(x,y,z, rstride = 3, cstride = 3)

ax1.set_xlabel('x axis')
ax1.set_ylabel('y axis')
ax1.set_zlabel('z axis')

plt.show()

如果你从一开始就关注这个教程的话，那么你已经学会了 Matplotlib 提供的大部分内容。 你可能不相信，但Matplotlib 仍然可以做很多其他的事情！ 请继续学习，你可以随时访问 Matplotlib.org，并查看示例和图库页面。

注：空间曲面的画法

# 二次抛物面 z = x^2 + y^2

x = np.linspace(-10, 10, 101)
y = x
x, y = np.meshgrid(x, y)
z = x ** 2 + y ** 2
ax = plot.subplot(111, projection='3d')
ax.plot_wireframe(x, y, z)
plot.show()

# 半径为 1 的球

t = np.linspace(0, np.pi * 2, 100)
s = np.linspace(0, np.pi, 100)
t, s = np.meshgrid(t, s)
x = np.cos(t) * np.sin(s)
y = np.sin(t) * np.sin(s)
z = np.cos(s)
ax = plot.subplot(111, projection='3d')
ax.plot_wireframe(x, y, z)
plot.show()