基于多个MPC的的调度控制器
1引言
本文J将对MATLAB自带的MPC例子进行详细剖析
MPC:Model Predictive Control Toolbox
开始设计工具:通过输入MATLAB命令:‘mpctool’开始设计工具。
下图1中的图形中左侧的三个栏目分别为受控对象模型(plant model)、模型预测控制器(Controllers)、仿真器(Scenarios)。

模型预测控制工具箱是一个图形用户界面的设计。这个GUI是控制和评估工具管理器GUI的一部分。见下图
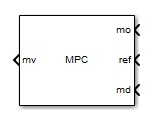
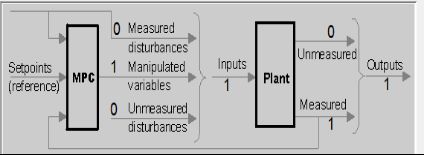
Mo(measured output):当前可测量的输出信号
Ref(Reference signa):参考信号
Md(optional measured disturbance signa):可选的测量干扰信号
Mv(optimal manipulated variables ):最优操纵变量
MPC一般通过求解一个二次规划(这里我们使用ord45)来计算最优操纵变量
一个简单的例子如下图所示:

2.多个MPC调度控制器解决方案
2.1系统描述
如果你的对象模型是非线性,设计一个控制器操作在一个特定的目标地区表现优异,但可能在其他地区表现不佳。补偿的常用方法是设计多个控制器,每个面向一个特定的操作条件的组合。他们之间切换实时随着情况的变化。获得这项技术的调度是一个传统的例子。下面的例子显示了如何协调多个模型预测控制器
该系统是由两个物体M1和M2分别连接到两个独立的弹簧k1和k2组成。假定当M1和M2碰撞的时候是完全非弹性碰撞。力F对于M1来说是拉力,这是可操纵变量( manipulated variable MV)。目标是使M1的位置y1跟踪给定参考位置r(Reference signa)。
当M1和M2分离时,M1自由地移动。发生碰撞的时候,由于是完全非弹性碰撞,所以M1 + M2一起移动。我们假设只有M1的位置和接触传感器提供反馈。后者是用来触发开关MPC控制器来选择MPC1还是MPC2。在这里,我们认为,M2的位置和速度的不可控。这这里,我们认为右方向为正方向。如下图 所示:
所示:
2.2模型参数
clear all
clc
M1=1; % M1的质量
M2=5; % M2的质量
k1=1; % 弹簧k1常数k
k2=0.1; % 弹簧k2常数k
b1=0.3; % 与空气的摩擦系数,与速度成正比
b2=0.8; % 摩擦系数
yeq1=10; % 刚性壁1的位置
yeq2=-10; % 刚性壁2的位置 2.3状态空间模型

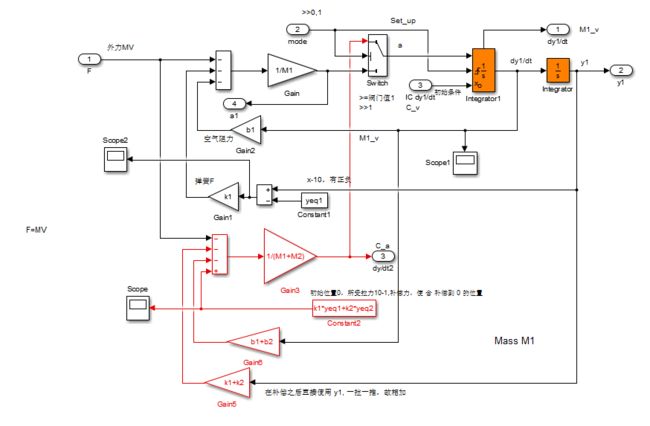
states:M1的位置和速度
MV:推力F
MD:物体1由弹簧的需求的力F和实际给出的F之间的常量误差,用来弥补弹簧弹力,使M在初始位置0上时,弹簧对其作用力为零。
MO:M1的位置
2.3.1当M1和M2没有接触时候的模型MPC1
%% 状态空间模型
% 当M1和M2不接触时候的状态模型.
A1=[0 1;-k1/M1 -b1/M1];
B1=[0 0;-1/M1 k1*yeq1/M1];
C1=[1 0];
D1=[0 0];
sys1=ss(A1,B1,C1,D1); %建立状态空间表达式
sys1=setmpcsignals(sys1,'MD',2); %第二个输入是可测量扰动【注】:
1.Sys = ss(a,b,c,d):用来描述连续性的状态空间模型
2.Setmpcsignals:设置MPC受控对象的的I/0信号模型。这个系统必须是线性时不变系统,’MD’:可测量的输入扰动,,第二个输入是可测量的输入扰动。如果没有指定的输入变量是MV
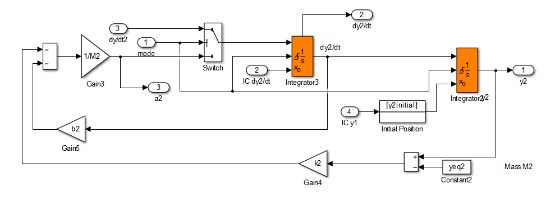
2.3.2当M1和M2连接在一起时候的模型MPC2
% 当M1和M2接触时候的状态模型.
A2=[0 1;-(k1+k2)/(M1+M2) -(b1+b2)/(M1+M2)];
B2=[0 0;-1/(M1+M2) (k1*yeq1+k2*yeq2)/(M1+M2)];
C2=[1 0];
D2=[0 0];
sys2=ss(A2,B2,C2,D2);
sys2=setmpcsignals(sys2,'MD',2);2.4 Multi-MPC控制设置
%% MPC仿真参数设置
Ts=0.2; % 采样时间
p=20; % 预测时域长度
m=1; % 控制时域长度
%% 建立MPC模型
MPC1=mpc(sys1,Ts,p,m); % 定义M1和M2分离的MPC模型
% 设置限制,F的大小不能为0,F斜率绝对值最大1000
MPC1.MV=struct('Min',0,'Max',Inf,'RateMin',-1e3,'RateMax',1e3);
MPC2=mpc(sys2,Ts,p,m); %定义M1和M2连接的MPC2模型
MPC2.MV=MPC1.MV; %系统1和系统2的控制限制一样2.5仿真参数设置
%% 仿真参数设置
Tstop=100; % 仿真时间
y1initial=0; % 物体1的初始位置
y2initial=10; % 物体2的初始位置
open_system('wc1'); % 调用wc1.MDL
disp('Start simulation by switching control between MPC1 and MPC2 ...');
set_param('wc1/signals','Open','On');%设置系统和模型的参数值
sim('wc1',Tstop);%开始动态系统仿真3.Simulatink实现
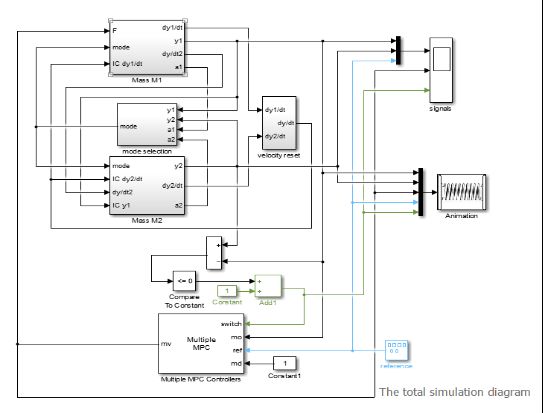
The total simulation diagram上面的部分模拟两个物体的运动,并且这种移动会在在示波器中以信号的方式显示出来。并且当M1的位置和加速度均大于M2的位置和加速度时,model输出布尔量true或者false;下半部分包含以下要素:
1.多个MPC控制器,。这有四个输入:可测量输出(mo), 参考(ref),可测量干扰(md)输入和独特的多个MPC控制器的功能块switch输入。
2.一脉冲发生器改变M1需要到达的位置 (控制器参考信号)。此脉冲发生器的输出是一个幅值为5的方波,频率是0.015每秒。
3.模拟传感器的接触。当switch输入1时,激活第一个控制器MPC1,这个时候M1和M2是分离的。当两个物体有相同的位置时,Compare to Constant的计算结果为1,通过Add1加法器的输出值为2,Multiple MPC Controllers的switch端口被输入2,自动启动第二个控制器MPC2。
4.解决方案评价
下图展示了仿真的过程:

4.1 MPC1与MPC2协同工作
下图展示了对于这个例子多个MPC控制器的仿真:
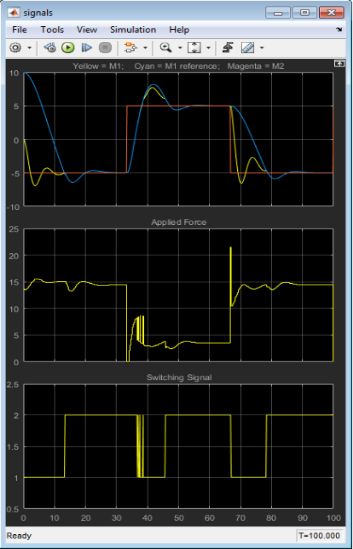
在图上面上,青色的线(就是我们M1需要的到达的位置,由reference产生)它从-5开始。的M1位置(黄色)从0开始出发。 在MPC1的控制下, M1移动迅速向所需的位置。M2(红色)从10开始开始朝着同一个方向移动
大约在t = 13秒,M2与M1发生完全非弹性碰撞。M1与M2连在一起。第三幅图显示了开关信号的变化,在这个瞬间从1到2,所以MPC2开始起作用。。
在M1+M2超过了从其所期望的位置时候,M2和M1仍连在一起。控制器MPC2调整作用力F(中间的图片)使M1+M2快速返回到所需的位置。当r突变到5时,效果一样是非常不错的
4.2 单个MPC1一直工作
假设我们的控制器MPC1运行在所有条件下
%再进行一次无论在什么情况下只用MPC1系统的实验
disp('Now repeat simulation by using only MPC1 ...');
MPC2save=MPC2; %先将MPC2保存起来
MPC2=MPC1; %用MPC2来代替MPC21
sim('wc1',Tstop); %动态系统仿真下图显示了MPC1单独工作的图像
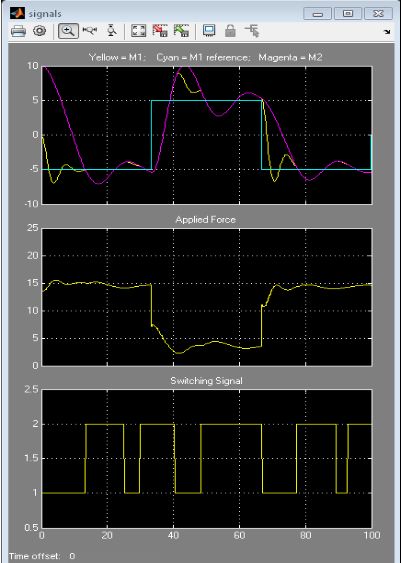
如果一直是MPC1的系统,力F不够,当M1和M2链连接在一起的时候,移动缓慢,当下一个转变发生时还不能到达所需的位置
4.3单个MPC2一直工作
%再进行一次无论在什么情况下只用MPC2系统的实验
disp('Now repeat simulation by using only MPC2 ...');
MPC1=MPC2save;
MPC2=MPC1;
sim('WC1',Tstop);假设我们的控制器MPC2运行在所有条件下
下图显示了MPC1单独工作的图像
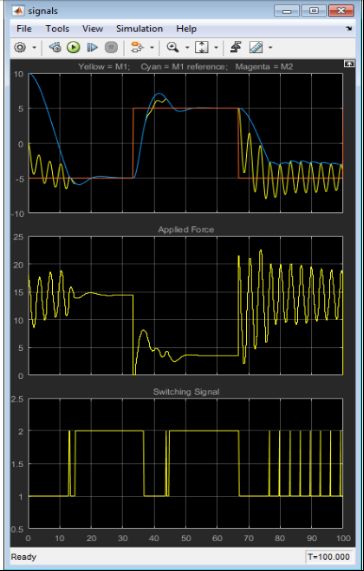
当M1和M2分开的时候,MPC2也依然使用,过度使用F,过度补偿,导致振荡产生。当M2和M1连接在一起的时候,移动更平稳,和预期一样。最后过渡造成特别严重的振荡。 M1和M2频繁的碰撞,M1不能到达所需的位置。
5.参考文献
[1] A. Bemporad, S. Di Cairano, I. V. Kolmanovsky, and D. Hrovat, “Hybrid
modeling and control of a multibody magnetic actuator for automotive applications,” in Proc. 46th IEEE(R) Conf. on Decision and Control, New Orleans, LA, 2007.
[2]http://cn.mathworks.com/help/mpc/gs/coordination-of-multiple-model-predictive-controllers.html#bs670e3-8
[3]李国勇,智能预测控制及其MATLAB实现.北京:电子工业出版社,2010.
6.附录
%% 多个MPC的的调度控制器
% clc
% clear all
%% 系统参数
clear all
clc
M1=1; % M1的质量
M2=5; % M2的质量
k1=1; % 弹簧k1常数k
k2=0.1; % 弹簧k2常数k
b1=0.3; % 与空气的摩擦系数,与速度成正比
b2=0.8; % 摩擦系数
yeq1=10; % 刚性壁1的位置
yeq2=-10; % 刚性壁2的位置
%% 状态空间模型
% 状态: M的速度和位置
% 被控变量:F
% 可测量的扰动:弹簧1的常熟;
% 测量输出: M1的位置
% 当M1和M2不接触时候的状态模型.
A1=[0 1;-k1/M1 -b1/M1];
B1=[0 0;-1/M1 k1*yeq1/M1];
C1=[1 0];
D1=[0 0];
sys1=ss(A1,B1,C1,D1); %建立状态空间表达式
sys1=setmpcsignals(sys1,'MD',2) ;%第二个输入是可测量扰动
% 当M1和M2接触时候的状态模型.
A2=[0 1;-(k1+k2)/(M1+M2) -(b1+b2)/(M1+M2)];
B2=[0 0;-1/(M1+M2) (k1*yeq1+k2*yeq2)/(M1+M2)];
C2=[1 0];
D2=[0 0];
sys2=ss(A2,B2,C2,D2);
sys2=setmpcsignals(sys2,'MD',2);
%% MPC仿真参数设置
Ts=0.2; % 采样时间
p=20; % 预测时域长度
m=1; % 控制时域长度
%% 建立MPC模型
MPC1=mpc(sys1,Ts,p,m); % 定义M1和M2分离的MPC模型
MPC1.MV=struct('Min',0,'Max',Inf,'RateMin',-1e3,'RateMax',1e3); % 设置限制,F的大小不能为0
MPC2=mpc(sys2,Ts,p,m); %定义M1和M2连接时候的MPC模型
MPC2.MV=MPC1.MV; %系统1和系统2的控制限制一样
%% 仿真参数设置
Tstop=100; % 仿真时间
y1initial=0; % 物体1的初始位置
y2initial=10; % 物体2的初始位置
open_system('WC1'); % 调用WC1.MDL
%% 开始三次仿真
%双系统MPC1和MPC2仿真实验
disp('Start simulation by switching control between MPC1 and MPC2 ...');
set_param('wc1/signals','Open','On');%设置系统和模型的参数值
sim('WC1',Tstop);%动态系统仿真
%再进行一次无论在什么情况下只用MPC1系统的实验
disp('Now repeat simulation by using only MPC1 ...');
MPC2save=MPC2; %先将MPC2保存起来
MPC2=MPC1; %用MPC2来代替MPC21
sim('WC1',Tstop);
%再进行一次无论在什么情况下只用MPC2系统的实验
disp('Now repeat simulation by using only MPC2 ...');
MPC1=MPC2save;
MPC2=MPC1;
sim('WC1',Tstop);
%% 关闭仿真窗口
% bdclose('WC1')
% close(findobj('Tag','WC1_demo'))
%% reference
%[1] A. Bemporad, S. Di Cairano, I. V. Kolmanovsky, and D. Hrovat, "Hybrid
% modeling and control of a multibody magnetic actuator for automotive
% applications," in Proc. 46th IEEE(R) Conf. on Decision and Control, New
% Orleans, LA, 2007.
%[2]http://cn.mathworks.com/help/mpc/gs/coordination-of-multiple-model-predictive-controllers.html#bs670e3-8
%[3]李国勇,智能预测控制及其MATLAB实现.北京:电子工业出版社,2010.