在几何图形中均匀随机取点算法总结及Delaunay三角剖分算法介绍
在工作中遇到一个需求,需要在圆形 矩形,三角形内随机,尽量均匀取点作为位置信息,但是random得到的信息有时候不是很满意。
这里讨论一下
第一种错误思路:
根据圆的解析式![]() (假设圆心在原点)我们可以先随机生成[-R, R]范围内横坐标x,然后生成
(假设圆心在原点)我们可以先随机生成[-R, R]范围内横坐标x,然后生成![]() 范围内的随机数y,(x,y)就是需要的点。
范围内的随机数y,(x,y)就是需要的点。
我们写程序模拟了该过程,从下图可以看出,我们可以看到当x靠近圆的边缘使,y的范围减小,因此两边边缘的点较密集,靠近圆心的点较稀疏。
上面的效果会造成在中心过度聚集的情况,可以使用二维随机点的做法,若落在圆形外则重新生成点。
可以求得:每次生成点时,该点有 ![]() 的概率在圆内
的概率在圆内
#!/usr/bin/env python
# _*_ coding:utf-8 _*_
import matplotlib.pyplot as plt
import random, math
x_values = []
y_values = []
'''
#会造成中心过度集中的情况
for i in range(1000):
r = random.randint(0,100) - 50
theta = random.randrange(0,10000)
x_values.append(r* math.cos(theta))
y_values.append(r * math.sin(theta))
# print(r,theta)
# print(theta)
'''
for i in range(1000):
x = random.randint(0,100) - 50
y = random.randint(0, 100) - 50
if x*x + y*y < 50*50:
x_values.append(x)
y_values.append(y)
'''
scatter()
x:横坐标 y:纵坐标 s:点的尺寸
'''
plt.scatter(x_values, y_values, s=4)
# 设置刻度标记的大小
plt.tick_params(axis='both', which='major', labelsize=14)
# 设置每个坐标轴的取值范围
plt.axis([-60, 60, -60, 60])
plt.show()同理,上面也解决了矩形内随机取点的问题,这个思路也可以用于三角形问题
当然对于超出三角形区域外的点,我们可以通过折叠使得改点重新落在三角形内部,而不是直接舍掉,这样省去重新生成而提高效率。
错误思路1:
对于三角形ABC和一点P,可以有如下的向量表示:
![]()
p点在三角形内部的充分必要条件是:1 >= u >= 0, 1 >= v >= 0, u+v <= 1。
先生成[0,1]的随机数u,然后生成[0, 1-u]内的随机数v,u、v生成后,就可以得到p点的坐标:
![]()
由下图可知,该算法生成的点在靠近A点处较浓密
错误思路2:
通过使用Trilinear 坐标来随机取点,不过这个方法得到的结果也是非均匀分布的,越中间越密集
(正确的但效率不很好)
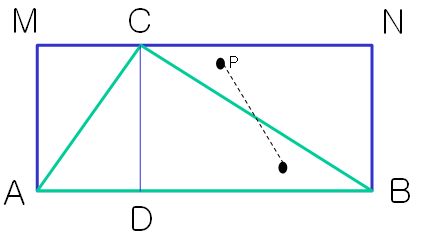
如图所示,三角形ABC有与之对应的矩形ABNM,且矩形面积是三角形的两倍,三角形ADC和CMA全等,CDB和BNC全等。
我们可以先生成矩形ABNM内的随机点P,如果P刚好在三角形ABC中,那么符合要求;如果P不在三角形ABC中,P要么在AMC中,要么在BNC中,如图P在BNC中,我们求P关于BC中点的的中心对称点,该点一定在三角形中。P在AMC中同理。这样可以保重三角形外的点都可以均匀的一一对应到三角形内部。
后面的代码中,为了简化计算,我们假设AB是平行X轴的。
对于生成任意多边形内的随机点,我们可以把它分割成三角形,再来生成随机点。
二维平面上判断点是否在三角形内
最近在项目中碰到的这个问题,在此记录一下。已知三角形的三个顶点坐标,判断某个点是否在三角形中(在三角形的边上,我们也视作在三角形中),本文给出了三种方法。
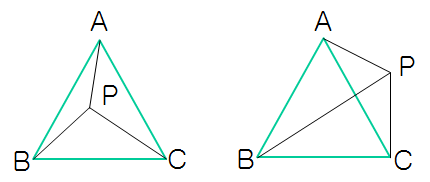
算法1
利用面积法,如上图所示,如果点P在三角形ABC的内部,则三个小三角形PAB, PBC, PAC的面积之和 = ABC的面积,反之则不相等。
已知三角形的三个顶点坐标求其面积,可以根据向量的叉乘,参考here。
该算法详见后面代码中的函数:IsPointInTriangle1
算法2
首先看一下这个问题,如何判断某两个点在某条直线的同一侧(代码中函数:IsPointAtSameSideOfLine)?
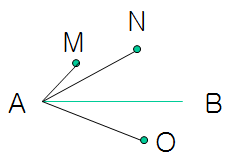
根据向量的叉乘以及右手螺旋定则,AB^AM (^表示叉乘,这里向量省略了字母上面的箭头符号)的方向为向外指出屏幕,AB^AN也是向外指出屏幕,但AB^AO的方向是向内指向屏幕,因此M,N在直线AB的同侧,M ,O在直线AB的两侧。实际计算时,只需要考虑叉积的数值正负
假设以上各点坐标为A(0,0), B(4,0), M(1,2), N(3,4), O(3,-4), 则:
AB^AM = (4,0)^(1,2) = 4*2 - 0*1 = 8
AB^AN = (4,0)^(3,4) = 4*4 – 0*3 = 16
AB^AO = (4,0)^(3,-4) = 4*-4 – 0*3 = –16
由上面的数值可知,可以根据数值的正负判断叉乘后向量的方向。即,如果叉积AB^AM 和 AB^AN的结果同号,那么M,N两点就在直线的同侧,否则不在同一侧。特殊地,如果点M在直线AB上,则AB^AM的值为0。(如果是在三维坐标系中,求出的叉积是一个向量,可以根据两个向量的点积结果正负来判断两个向量的是否指向同一侧) 本文地址
以上的问题解决了,就很容易的用来判断某个点是否在三角形内,如果P在三角形ABC内部,则满足以下三个条件:P,A在BC的同侧、P,B在AC的同侧、PC在AB的同侧。某一个不满足则表示P不在三角形内部。
该算法详见后面代码中的函数:IsPointInTriangle2
算法3
该方法也用到了向量。对于三角形ABC和一点P,可以有如下的向量表示:
![]()
p点在三角形内部的充分必要条件是:1 >= u >= 0, 1 >= v >= 0, u+v <= 1。
已知A,B,C,P四个点的坐标,可以求出u,v,把上面的式子分别点乘向量AC和向量AB
解方程得到:
解出u,v后只需要看他们是否满足“1 >= u >= 0, 1 >= v >= 0, u+v <= 1”,如满足,则,p 在三角形内。
(u = 0时,p在AB上, v = 0时,p在AC上,两者均为0时,p和A重合)
该算法详见后面代码中的函数:IsPointInTriangle3
算法4
该算法和算法2类似,可以看作是对算法2的简化,也是用到向量的叉乘。假设三角形的三个点按照顺时针(或者逆时针)顺序是A,B,C。对于某一点P,求出三个向量PA,PB,PC, 然后计算以下三个叉乘(^表示叉乘符号):
t1 = PA^PB,
t2 = PB^PC,
t3 = PC^PA,
如果t1,t2,t3同号(同正或同负),那么P在三角形内部,否则在外部。
该算法详见后面代码中的函数:IsPointInTriangle4
经过测试,算法4最快,算法3次之,接着算法2,算法1最慢。直观的从计算量上来看,也是算法4的计算量最少。
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
最优三角形内部随机
另一种三角形内随机生成点的思路更简洁
通过算法
P = (1 - sqrt(r1)) * A + sqrt(r1) * (1 - r2) * B + sqrt(r1) * r2 * C,
A, B, C分别是三角形的三个顶点,r1, r2 是两个[0, 1]的随机数
大家对这个算法的由来感兴趣的话可以去看看Princeton大学发布的报告:
http://www.cs.princeton.edu/~funk/tog02.pdf
令s,t在区间[0,1]之间取值,随机点QQ的值依靠以下算法获得:
a←1−√t;
b←(1−s)√t;
c←s√t;
Q←aA+bB+cC;
在以上的算法中,我们使用变量tt来获得一条平行于BCBC并且与ABAB和ACAC相交的直线,并且在这条线段上根据ss来获得这个点。
需要注意的是这里使用到了t√t而不是简单的tt来进行操作。这是因为均匀分布是根据面积来判定的,因此上层三角形的面积是与高度的平方成正比,因此此处需要使用√t来进行操作。
#!/usr/bin/env python
# _*_ coding:utf-8 _*_
import matplotlib.pyplot as plt
import random, math
x_values = []
y_values = []
A = [0, 1]
B = [3, 1]
C = [1, 2]
for i in range(10000):
t = random.random()
s = random.random()
a = 1 - math.sqrt(t)
b = (1 - s) * math.sqrt(t)
c = s * math.sqrt(t)
xx = a * A[0] + b * B[0] + c * C[0]
yy = a * A[1] + b * B[1] + c * C[1]
x_values.append(xx)
y_values.append(yy)
'''
scatter()
x:横坐标 y:纵坐标 s:点的尺寸
'''
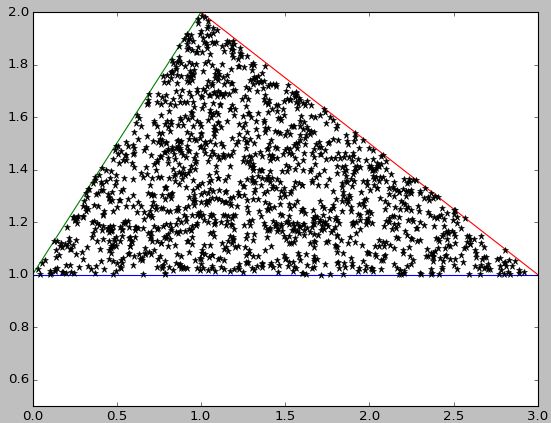
plt.scatter(x_values, y_values, s=4)
# 设置刻度标记的大小
plt.tick_params(axis='both', which='major', labelsize=14)
# 设置每个坐标轴的取值范围
plt.axis([0, 3, 1, 2])
plt.show()
Method 2
令s,t在区间[0,1]之间取值,随机点Q的值依靠以下算法获得:
if s+t>1 then
begin
s←1−s
t←1−t
end
a←1−s−t;
b←s;
c←t;
Q←aA+bB+cC;
如果我们把if语句去掉,实际上上面的算法是求出了一个在平行四边形(A,B,C,B+C−A)内的随机点。

如果这个随机点位于三角形(B,C,B+C−A)中,则通过BC边反射到三角形(A,B,C)内即可。

推演到高维
Method 1可以很方便得扩展到高维,例如,如果我们需要在四面体内生成均匀的随机点,则只需要三个随机数。第一个数获得与底面平行的面,而后两个数则在这个面上进行随机点选取。
Method 2想要扩展到高维就麻烦不少了。给出r,s,tr,s,t三个点,我们可以使用这三个点来获得一个平行六面体中的随机点。但是平行六面体想要切割成两个全等的四面体是挺麻烦的,因此直接取点然后进行反射的方法不太实际。
但是实际上我们可以进行r+s+t>1r+s+t>1的条件判断来筛选出那些在六面体中而不在原四面体中的点,直接忽视之即可。
作为推广,其实多个多边形也是可以这样生成的,只需要分割为多个三角形,根据三角形面积比例,控制样本比例即可
另外的思路是选多边形的外接圆,随机取点,若在多边形外部则舍掉,该方法需要判断点是不是在多边形内部
计算方法是射线法,计算交点个数:
def isInsidePolygon(pt, poly):
c = False
i = -1
l = len(poly)
j = l - 1
while i < l - 1:
i += 1
print(i, poly[i], j, poly[j])
if ((poly[i]["lat"] <= pt["lat"] and pt["lat"] < poly[j]["lat"]) or (
poly[j]["lat"] <= pt["lat"] and pt["lat"] < poly[i]["lat"])):
if (pt["lng"] < (poly[j]["lng"] - poly[i]["lng"]) * (pt["lat"] - poly[i]["lat"]) / (
poly[j]["lat"] - poly[i]["lat"]) + poly[i]["lng"]):
c = not c
j = i
return c
if __name__ == '__main__':
abc = [{'lat': 1, 'lng': 1}, {'lat': 1, 'lng': 4}, {'lat': 3, 'lng': 7}, {'lat': 4, 'lng': 4}, {'lat': 4, 'lng': 1}]
print(isInsidePolygon({'lat': 2, 'lng': 5}, abc))
扩展部分:
三角剖分算法(delaunay)
开篇
![]()
在做一个Low Poly的课题,而这种低多边形的成像效果在现在设计中越来越被喜欢,其中的低多边形都是由三角形组成的。
而如何自动生成这些看起来很特殊的三角形,就是本章要讨论的内容。
项目地址: https://github.com/zhiyishou/polyer
Demo:https://zhiyishou.github.io/Polyer
选择
其实最先是由很多离散的点组成,基于这个确定的点集,将点集连接成一定大小的三角形,且分配要相对合理,才能呈现出漂亮的三角化。
这时则要求使用三角剖分算法(Delaunay),引于百度百科《Delaunay三角剖分算法》对Delaunay三角形的定义为:
【定义】三角剖分:假设V是二维实数域上的有限点集,边e是由点集中的点作为端点构成的封闭线段, E为e的集合。那么该点集V的一个三角剖分T=(V,E)是一个平面图G,该平面图满足条件:
1.除了端点,平面图中的边不包含点集中的任何点。
2.没有相交边。
3.平面图中所有的面都是三角面,且所有三角面的合集是散点集V的凸包。
在实际中运用的最多的三角剖分是Delaunay三角剖分,它是一种特殊的三角剖分。先从Delaunay边说起:
【定义】Delaunay边:假设E中的一条边e(两个端点为a,b),e若满足下列条件,则称之为Delaunay边:存在一个圆经过a,b两点,圆内(注意是圆内,圆上最多三点共圆)不含点集V中任何其他的点,这一特性又称空圆特性。
【定义】Delaunay三角剖分:如果点集V的一个三角剖分T只包含Delaunay边,那么该三角剖分称为Delaunay三角剖分。
【定义】假设T为V的任一三角剖分,则T是V的一个Delaunay三角剖分,当前仅当T中的每个三角形的外接圆的内部不包含V中任何的点。
![]()
如图,将离散点联结成Delaunay三角形
算法
关于Delaunay三角形的算法,有翻边算法、逐点插入算法、分割合并算法、Bowyer-Watson算法等。
而在这几种算法中,逐点插入算法比较简单、易懂,在本文中只针对该算法进行讨论,该算法也是目前使用最为广泛的Delaunay算法。
在该算法中,主要应用Delaunay三角形【定义4】,理解下来就是每一个三角形的外接圆圆内不能存在点集内的其它任何一点,而有时候会出现点在外接圆上的情况,这种情况被称为“退化”。
在文章《Triangulate》里对该方法进行了分析,并提出了伪代码思路:
subroutine triangulate
input : vertex list
output : triangle list
initialize the triangle list
determine the supertriangle
add supertriangle vertices to the end of the vertex list
add the supertriangle to the triangle list
for each sample point in the vertex list
initialize the edge buffer
for each triangle currently in the triangle list
calculate the triangle circumcircle center and radius
if the point lies in the triangle circumcircle then
add the three triangle edges to the edge buffer
remove the triangle from the triangle list
endif
endfor
delete all doubly specified edges from the edge buffer
this leaves the edges of the enclosing polygon only
add to the triangle list all triangles formed between the point
and the edges of the enclosing polygon
endfor
remove any triangles from the triangle list that use the supertriangle vertices
remove the supertriangle vertices from the vertex list
end
其方法虽然可实现三角化,但是效率还是不太高
在看过https://github.com/ironwallaby/delaunay该js也是基于该伪代码进行编写的,但是作者在其中进行了一次排序优化,使得代码运行效率得到了提高
优化后的伪代码为:
input: 顶点列表(vertices) //vertices为外部生成的随机或乱序顶点列表
output:已确定的三角形列表(triangles)
初始化顶点列表
创建索引列表(indices = new Array(vertices.length)) //indices数组中的值为0,1,2,3,......,vertices.length-1
基于vertices中的顶点x坐标对indices进行sort //sort后的indices值顺序为顶点坐标x从小到大排序(也可对y坐标,本例中针对x坐标)
确定超级三角形
将超级三角形保存至未确定三角形列表(temp triangles)
将超级三角形push到triangles列表
遍历基于indices顺序的vertices中每一个点 //基于indices后,则顶点则是由x从小到大出现
初始化边缓存数组(edge buffer)
遍历temp triangles中的每一个三角形
计算该三角形的圆心和半径
如果该点在外接圆的右侧
则该三角形为Delaunay三角形,保存到triangles
并在temp里去除掉
跳过
如果该点在外接圆外(即也不是外接圆右侧)
则该三角形为不确定 //后面会在问题中讨论
跳过
如果该点在外接圆内
则该三角形不为Delaunay三角形
将三边保存至edge buffer
在temp中去除掉该三角形
对edge buffer进行去重
将edge buffer中的边与当前的点进行组合成若干三角形并保存至temp triangles中
将triangles与temp triangles进行合并
除去与超级三角形有关的三角形
end大多数同学看过伪代码后还是一头雾水,所以用图来解释这个过程,我们先用三点来做实例:
![]()
如图,随机的三个点
根据离散点的最大分布来求得随机一个超级三角形(超级三角形意味着该三角形包含了点集中所有的点)
我的方法是根据相似三角形定理求得与矩形一半的小矩形的对角三角形,扩大一倍后则扩大后的直角三角形斜边经过点(Xmax,Ymin)
但是为了将所有的点包含在超级三角形内,在右下角对该三角形的顶点进行了横和高的扩展,并要保证这个扩展三角形底大于高,才能实现包含
这样求得的超级三角形不会特别大使得计算复杂,而且过程也简单,并将超级三角形放入temp triangles中
![]()
接下来就像是伪代码中描述的那样,对temp triangle中的的三角形遍历画外接圆,这时先对左边的第一个点进行判断,其在圆内
所以该三角形不为Delaunay三角形,将其三边保存至edge buffer中,temp triangle中删除该三角形
![]()
将该点与edge buffer中的每一个边相连,组成三个三角形,加入到temp triangles中
![]()
再将重复对temp triangles的遍历并画外接圆,这时使用的是第二个点来进行判断
- 该点在三角形1外接圆右侧,则表示左侧三角形为Delaunay三角形,将该三角形保存至triangles中
- 该点在三角形2外接圆外侧,为不确定三角形,所以跳过(后面会讲到为什么要跳过该三角形),但并不在temp triangles中删除
- 该点在三角形3外接圆内侧,则这时向清空后的edge buffer加入该三角形的三条边,并用该点写edge buffer中的三角边进行组合,组合成了三个三角形并加入到temp triangles中
![]()
再次对temp triangles进行遍历,这里该数组里则含有四个三角形,一个是上次检查跳过的含有第一个点的三角形和新根据第二个点生成的三个三角形
- 该点在三角形1外接圆右侧,则该三角形为Delaunay三角形,保存至triangles中,并在temp triangles中删除
- 该点在三角形2外接圆外侧,跳过
- 该点在三角形3外接圆内侧,将该三边保存至temp buffer中,并在temp triangles中删除
- 该点在三角形4外接圆内侧,将该三边保存至temp buffer中,并在temp triangles中删除
这时,temp buffer 中有六条边,triangles中有两个三角形,temp triangles中有1个三角形
对temp buffer中的六条边进行去重,得到五条边,将该点与这五条边组合成五个三角形并加入到temp triagnles 中,这时temp triangles中有6个三角形
![]()
由于三个点已经遍历结束,到了不会再对第三个点形成的三角形做外接圆,这时则将triangles与temp trianlges合并,合并后的数组表示包含已经确定的Delaunay三角形和剩下的三角形
这时除去合并后数组中的和超级三角形三个点有关的所有三角形,即进行数组坐标的限定,则得到了最后的结果:
![]()
这是用最少的三个点来做讲解,点数越多的话计算量会越大,但是都是在上面步骤下进行的。
问题
在用点对三角形外接圆位置关系进行判断的时候,为什么点在外接圆的右侧的话可以确定该三角形是Delaunay三角形
而当点外接圆的外侧且非右侧时,为什么要路过三角形,不把该三角形确定为Delaunay三角形呢?
首先,我们在开始的时候对原始方法进行优化时,我们增加了一个indices数组来操作vertices,并对indices依据vertices的x坐标进行了从小到大的排序
则我们在后面遍历点时是从点集的最左侧开始的,如图:
![]()
当遍历下一个点时,该点在外接圆的右侧,则表示以后所有的点都在该外接圆的右侧,则保证了Delaunay三角形的空圆特性
而当点在外接圆外,并非外接圆右侧时,如图:
![]()
在该三角形的外切圆中,当遍历到点1时,符合在外侧的条件,但是不能确定后面所有的点都保持在外接圆外侧
如果说该三角形就为Delaunay三角形的话,如图中的点2及后面可能出现的点很有可能出现在圆内,而使该三角形被按边分解
在我们的算法中,如果碰到在点在外侧且非右侧的话,会跳过,该三角形一直在temp triangles中被检验,直到碰到下一个点在圆内或圆右才会从temp triangles中去除,进行后面的操作
而当点在圆上时,也是根据在圆内的方法对其进行操作,实际情况中会出现这种情况,上文也讲过,称为“退化”。
最后,附一张delaunay的随机demo图:
![]()
#!/usr/bin/env python
# _*_ coding:utf-8 _*_
'''
随机生成1000个点,选取任意3个点组成三角形,问,如何判断其余的997个点在三角形内或外?
'''
import numpy as np
import random
# 定义点
class Vertex(object):
def __init__(self, x, y):
self.x = x
self.y = y
def __str__(self):
return ("x坐标:%s,y坐标:%s" % (self.x, self.y))
# "Freind : %s" %self.name 返回多个参数啊
# 定义三角形
class Triangle(object):
def __init__(self, A, B, C):
self.A = A
self.B = B
self.C = C
def __str__(self):
return ("A点:%s B点:%s C点:%s" % (self.A, self.B, self.C))
# 判断构建的三角形是否满足三角形条件,即面积是否为零
def isTriangle(self):
arr = np.array([[self.A.x, self.A.y, 1], [self.B.x, self.B.y, 1], [self.C.x, self.C.y, 1]])
s = abs(0.5 * np.linalg.det(arr))
return False if s == 0 else True
# 判断一个点是否在三角形内,即该点与三角形任意两点构成的面积不为0且面积和为外部大三角形面积之和
def isInTriangle(self, D):
arr1 = np.array([[self.A.x, self.A.y, 1], [self.B.x, self.B.y, 1], [self.C.x, self.C.y, 1]])
sumAera = 0.5 * np.linalg.det(arr1)
arr2 = np.array([[self.A.x, self.A.y, 1], [self.B.x, self.B.y, 1], [D.x, D.y, 1]])
s1 = 0.5 * np.linalg.det(arr2)
arr3 = np.array([[self.A.x, self.A.y, 1], [D.x, D.y, 1], [self.C.x, self.C.y, 1]])
s2 = 0.5 * np.linalg.det(arr3)
arr4 = np.array([[D.x, D.y, 1], [self.B.x, self.B.y, 1], [self.C.x, self.C.y, 1]])
s3 = 0.5 * np.linalg.det(arr4)
if s1 != 0 and s2 != 0 and s3 != 0 and abs(s1 + s2 + s3 - sumAera) < 0.000001:
return True
else:
return False
if __name__ == '__main__':
# 产生1000个点且存储起来
arrOfVertex = []
for i in range(1000):
tempx = random.randint(1, 100)
tempy = random.randint(1, 100)
tempVertex = Vertex(tempx, tempy)
arrOfVertex.append(tempVertex)
# 在这1000个点中随机选取3个点且保证这三个点构成一个三角形
k, j, m = random.randint(0, 999), random.randint(0, 999), random.randint(0, 999)
selectedTriangle = Triangle(arrOfVertex[k], arrOfVertex[j], arrOfVertex[m])
while not selectedTriangle.isTriangle():
k, j, m = random.randint(0, 999), random.randint(0, 999), random.randint(0, 999)
selectedTriangle = Triangle(arrOfVertex[k], arrOfVertex[j], arrOfVertex[m])
# 判断点是否在三角形中,且用一个数组存储起来
arrOfJudge = []
sum = 0
for i in range(1000):
temp = selectedTriangle.isInTriangle(arrOfVertex[i])
print(arrOfVertex[i], end=" ")
if temp: sum += 1
arrOfJudge.append(temp)
print("选取的是否为三角形:%s" % selectedTriangle.isTriangle())
print(arrOfJudge)
print("在三角形内部的比例为:%s %%" % (sum / 10))
# a = Vertex(1, 1)
# b = Vertex(2, 2)
# c = Vertex(3, 3)
# print(a)
# tri = Triangle(a, b, c)
# print(tri)
# print(tri.isTriangle())