图解最长公共子序列LCS问题
很多人在上学的时候都有过对毕业论文进行查重的经历,一般可以通过CNKI,知网等平台提交自己的论文,平台将论文与其他论文进行匹配查重,最终得到一个相似度。不知大家对于查重问题有没有思考过,他背后是如何实现的呢?难道就是找到相似的字符串匹配就可以吗?本篇文章就带大家了解一种可以解决这个问题的经典算法。
本文主要主要包含以下三方面:
-
什么是LCS
-
如何实现LCS计算
-
LCS的使用场景
1. 什么是LCS
最长公共子序列,英文名称为Longest Common Subsequencem, 简写为LCS。针对它的求解属于动态规划算法中的典型代表,算法主要的目的就是为了求解两个序列中最长的子序列,这里很多人经常与最长公共子串问题搞混。我们后面通过一个实例来介绍下两者的区别。
这里我们首先要知道什么是子序列, 假设有字符串“ABCBDAB“,针对该字符串的子序列既可以是相互连接在一起的:
-
ABC
-
ABCBD
-
BCBD
-
CBDA
-
...
也可以是不连接在一起,但是保持前后顺序的:
-
BBA
-
CDAB
-
BCAB
-
ACDB
-
...
所以子序列这里最关键的是前后顺序,至于是否连接在一起则不重要。
如果是针对字符串相连接情况进行的算法处理,那是在求解最长公共子串,可以参考之前介绍的SuffixTrie结构来完成,在此不做过多介绍。
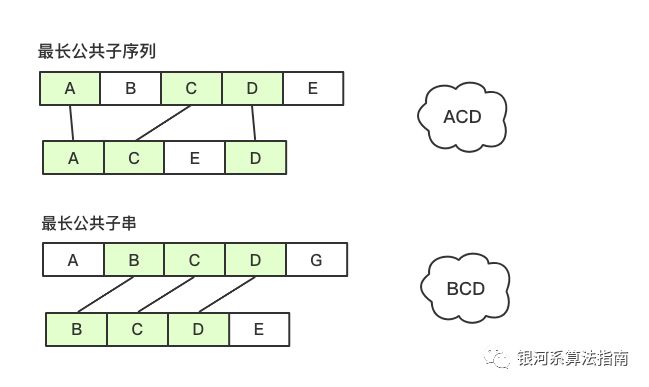
LCS的一个简单的实例如下图所示:两个序列“ABCDE”和“ACED“他们的LCS为图中标记颜色的子序列,共同的子序列为”ACD“, 这里是不连续的但是在两个序列中前后顺序一致的序列。
这个序列比较短的情况下,我们通过观察就可以发现,但是如何才能通过程序的方式表达出来呢,毕竟哪怕我们只有十几个元素情况下,已经很难通过观察发现其中的LCS了
2、如何计算LCS
如果我们通过暴力的方式来解这个问题,那么需要多少计算量呢?我们先来看下子序列的个数。
-
字符串长度是1,子序列只有一个,也就是字符串本身。
-
字符串长度为2,比如字符串AB,子序列的包含:A, B, AB三个。
-
字符串长度为3 ,比如字符串ABC, 子序列包含:A,B,C,AB,BC,AC,ABC七个。
结论:当长度为N的时候,子序列的数量为2的N次方-1 ,随着长度的增加,其子序列的长度将呈现为指数增加。对于数据量大的时候,这是非常不可取的一种计算方式。
关于LCS定义部分,我们提到了LCS属于动态规划算法问题,动态规划的两个典型的特征是:
问题的最优解包含其子问题的最优解。
子问题空间有限,不会生成无限子问题,且存在后续计算上的重叠。
如果之前没有接触过动态规划也没有关系,稍后我们通过例子来慢慢介绍。
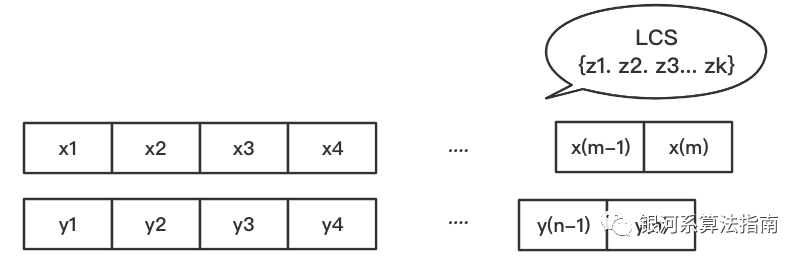
假设我们有两个序列,需要求解LCS, 分别是下图的{x1,x2...x(m)}序列和{y1,y2,...y(n)}序列,一个长度为m, 一个长度为n。为了求解当前两个序列的LCS, 我们可以将其拆分为较短序列的子问题来解决,同时子问题也可以继续向下拆分,直到序列为空。
这里我们推导一下计算子问题的流程:
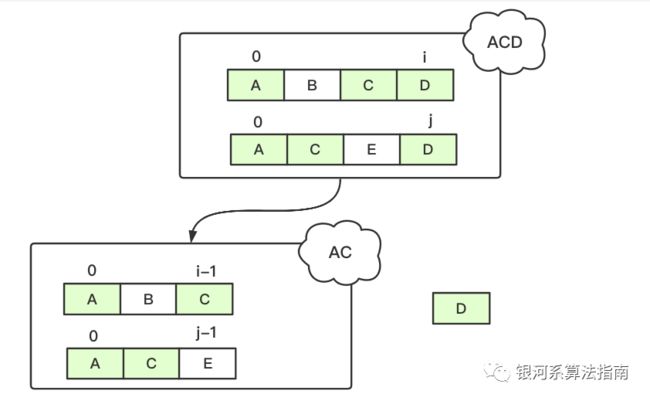
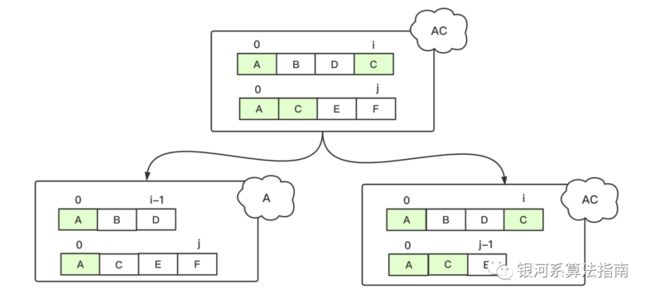
(1)假设两个序列的最后两个值x(m)=y(n), 那么序列的LCS实际上是原有的较小的子序列{x1,x2 .... x(m-1)} 和 {y1,y2, y3... y(n-1)}序列的LCS的值加上该相等值,因为最后值相同且顺序都在尾部,因此这个值必然属于原LCS一部分,存在x(m)=y(n)=z(k1)。
举个例子就可以看出来了,对于序列 “ABCD”和“ACED”两个序列的LCS为“ACD“, 这个时候尾部值相同。都去掉的话,相当于LCS也减少了一个值,因此当前序列LCS长度符合LCS[i, j ] = LCS(i-1, j-1) + 1
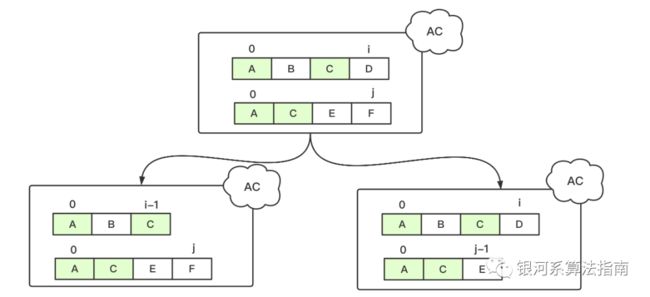
(2) 假设x(m+1) != y(n+1), 那么新的序列LCS应该是两对子序列的LCS最大值。表达式为 LCS[i, j ] = max(LCS(i-1, j), LCS(j-1)) 。由于尾部的两个值不相同,必然至少有一个是不被包含在LCS中或者两个都不在LCS的。
我们还是通过一个实例看一下:对于序列 “ABCD”和“ACEF”两个序列的LCS为“AC“, 这个时候尾部的D和F值不相同,满足上面的等式。
还有一种情况,去掉的值中包含了LCS一部分,比如序列”ABDC“和”ACEF“中尾部的两个值不同,但是第一个序列中的C属于LCS一部分。这时候仍旧满足上面的等式:
用下面的表达式表示就是:
如果知道了序列的表达式,那我们在求解的过程中可以通过一些矩阵的方式来完成计算和追溯结果。
我们通过一个稍微复杂点的序列求解过程来介绍下如何通过一个中间矩阵来求解上述的表达式。假设有序列A = ”ABCBDAB “ 和 序列 B= ”BDCABA“ , 我们首先初始化一个二维矩阵, 这个矩阵在处理的时候按照下面的规则处理:
-
二维矩阵的行高为M+1, 其中M为序列A的长度。列高为N+1,其中N为序列B的长度
-
如果矩阵中xi == yj , 则更新当前值为对角值+1, 并填充一个”↖“
-
如果矩阵中xi != yj 则更新当前值为上面的值和左面的值的最大值,并填充一个方向箭头,指向最大值。但如果左边的值和上面的值相同,则指向上面的值(此条件包含等于关系)
这里我们逐行处理表格, 对于第一行的处理完成后,其中存在一个相同的值,这是我们更新值,对角值为颜色标记为红色的方块。按照上述规则处理完成后如下面的右图所示。
依次处理完成后,整个的二维矩阵如下面所示:
创建该矩阵的程序如下面所示, 传递的参数为两个字符串数组,函数的目的为了获取上面的矩阵,结果返回两个二维矩阵,第一个用于存储箭头方向,第二个用于存储数值。
矩阵最右下角的值就是LCS的长度,这里是4表示为长度为四个字母, 但是如何获得这个LCS呢?这里我们只需要跟随箭头的方向就可以获取到最长的序列。跟随的规则如下:
-
从最右下角开始进行矩阵遍历
-
如果遇到一个向上的箭头,则移动到上一层的方块(绿色标记)
-
如果遇到一个向左的箭头,则移动到左边方块(绿色标记)
-
如果遇到一个”↖“箭头, 则该值为LCS的一部分(红色标记)。
回溯的程序代码如下, 程序参数为包含箭头的二维数组(上面的程序返回的第一个值),数组A序列,以及i, j 分别代表序列长度,这里是递归调用。第一次调用的时候传递的值i和j分别为数组A和B的长度即可。
3. 典型的使用场景
(1) DNA序列本身可以看做是由「A, C, G, T」四个字符组成的字符串,可以使用LCS算法为两个DNA序列做相似度匹配, 查找到两个DNA序列的LCS,可以知道两者之间的差距。
(2) 论文相似度查重, 检查两篇论文中相似地方,从而发现是否有抄袭的嫌疑
(3) Git系统中代码的比对算法Git-diff
通过上面的介绍,或许大家对于LCS的求解有了一定的认识,也对于如何实现论文查重的实现有一定的理解了吧。 大家对于算法和日常使用感兴趣的话,可以扫描下面的二维码来订阅我的个人公众号,感谢大家的阅读。
![]()