LeetCode - 回文串（序列）类总结（dp解法）

• 子串与子序列
  （1）字符子串：指的是字符串中连续的n个字符，如abcdefg中，ab，cde，fg等都属于它的字串。
  （2）字符子序列：指的是字符串中不一定连续但先后顺序一致的n个字符，即可以去掉字符串中的部分字符，但不可改变其前后顺序。如abcdefg中，acdg，bdf属于它的子序列，而bac，dbfg则不是，因为它们与字符串的字符顺序不一致。
    (3) 公共子序列：如果序列C既是序列A的子序列，同时也是序列B的子序列，则称它为序列A和序列B的公共子序列。如对序列 1,3,5,4,2,6,8,7和序列 1,4,8,6,7,5 来说，序列1,8,7是它们的一个公共子序列。最长公共子序列（LCS）：就是A和B的公共子序列中长度最长的（包含元素最多的），最长公共子序列（LCS）也不一定唯一，但是长度一定。

一. 最长回文子串： 给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
示例 ：
输入: “babad”
输出: “bab”
注意: “aba” 也是一个有效答案。

class Solution {
public:
	string longestPalindrome(string s) {
		int length = s.size();
		if (length == 0){
			return s;
		}
		int maxCount = 0;
		int left = 0;
		int right = 0;
		vector<vector<bool>> dp(length, vector<bool>(length,false));
		for (int i = 0; i < length; i++)
		{
			for (int j = i; j >= 0; j--){
				dp[i][j] = (s[i] == s[j]) && ((i - j < 3) || dp[i-1][j+1]);
				if (dp[i][j] && (i - j + 1>maxCount))
				{
					maxCount = i - j + 1;
					left = j;
					right = i;
				}
			}
		}
		return s.substr(left, right-left+1);
	}
};

---

二. 回文子串： 给定一个字符串，你的任务是计算这个字符串中有多少个回文子串。具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被计为是不同的子串。
示例 :
输入: “abc”
输出: 3
解释: 三个回文子串: “a”, “b”, “c”.

class Solution {
public:
    int countSubstrings(string s) {
        int length = s.size();
		if (length == 0){
			return 0;
		}
		int count = 0;
	
		vector<vector<bool>> dp(length, vector<bool>(length,false));
		for (int i = 0; i < length; i++)
		{
            count++;
			for (int j = i-1; j >= 0; j--){
				dp[i][j] = (s[i] == s[j]) && ((i - j < 3) || dp[i-1][j+1]);
				if (dp[i][j])
				{
					count ++;
                }
			}
		}
		return count;
    }
};

---

三. 最长回文子序列: 给定一个字符串s，找到其中最长的回文子序列。可以假设s的最大长度为1000。
示例 :输入:“bbbab” , 输出:4

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        if(s.empty()) return 0;
        int n=s.size();
        vector<vector<int> > dp(n,vector<int>(n,0));
        for(int j=0;j<n;j++){
            dp[j][j]=1;
            for(int i=j-1;i>=0;i--){
                if(s[i]==s[j]) dp[i][j]=dp[i+1][j-1]+2;
                else dp[i][j]=max(dp[i+1][j],dp[i][j-1]);
            }
        }
        return dp[0][n-1];
    }
};

---

四. 回文对: 给定一组唯一的单词， 找出所有不同 的索引对(i, j)，使得列表中的两个单词， words[i] + words[j] ，可拼接成回文串。
示例 :
输入: [“abcd”,“dcba”,“lls”,“s”,“sssll”]
输出: [[0,1],[1,0],[3,2],[2,4]]
解释: 可拼接成的回文串为 [“dcbaabcd”,“abcddcba”,“slls”,“llssssll”]
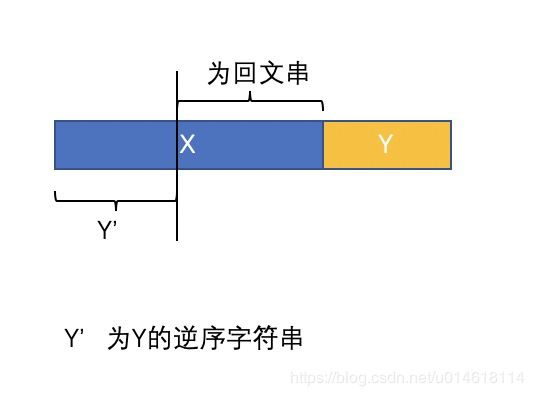
分析：根据回文字符串的性质，我们可以不用暴力枚举出所有字符串对。对于一个字符串对(x, y)(x,y), 若想要字符串x+y是一个回文字符串，则必须满足以下条件之一：
1.当x.length()≥y.length()时, 字符串x的y.length()长度的前缀与y的逆序相等，且字符串x去除长度为y.length()的前缀后，余下的部分也是一个回文字符串。
2.当x.length() < y.length()时,与情况一正相反。如下图所示，要分析Y在X前，Y在X后的两种情况。

class Solution {
public:
    bool f(string& s,int left,int right){
        while(left<right){
            if(s[left++]!=s[right--]) return false;
        }
        return true;
    }
    vector<vector<int>> palindromePairs(vector<string>& words) {
        unordered_map<string,int> m;
        set<int> s;
        int n=words.size();
        for(int i=0;i<n;i++){
            m[words[i]]=i;
            s.insert(words[i].size());
        }
        vector<vector<int>> res;
        for(int i=0;i<n;i++){
            string tmp=words[i];
            reverse(tmp.begin(),tmp.end());
            if(m.count(tmp)&&m[tmp]!=i){
                res.push_back({m[tmp],i});
            }
            int length=tmp.size();
            for(auto it=s.begin();*it!=length;it++){
                int d=*it;
                if(f(tmp,0,length-d-1)&&m.count(tmp.substr(length-d))){
                    res.push_back({i,m[tmp.substr(length-d)]});
                }
                if(f(tmp,d,length-1)&&m.count(tmp.substr(0,d))){
                    res.push_back({m[tmp.substr(0,d)],i});
                }
            }
        }
        return res;
    }
};

---

五. 回文排列: 给定一个字符串，判断该字符串中是否可以通过重新排列组合，形成一个回文字符串。

示例 1：输入: “code”，输出: false
示例 2：输入: “aab”，输出: true

// 只有0个或1个字符出现奇数次，其余出现偶数次
class Solution {
public:
    bool canPermutePalindrome(string s) {
        unordered_map<char, int> m;
        for(char c:s)
            m[c]+=1;
        int odd = 0;
        for(auto it = m.begin(); it!=m.end();++it)
            if(it->second % 2 == 1)
                odd ++;
        return (odd == 0) || (odd == 1);
    }
};

---

六、给定一个字符串 s，你可以通过在字符串前面添加字符将其转换为回文串。找到并返回可以用这种方式转换的最短回文串。
示例 1:输入: “aacecaaa”, 输出: “aaacecaaa”
示例 2:输入: “abcd”, 输出: “dcbabcd”
分析：采用字符串匹配KMP算法及求next值算法。先求s字符串首字符开始的最大回文串的长度length，拼接s串length下标后的字符串的翻转就是最短回文串。先创建临时字符串temp(s+rev(s)),再求出temp字符串的next数组，next[temp.size]就是s字符串首字符开始的最大回文串的长度。（KMP匹配的参考链接如下）
参考链接1
参考链接2

   /*思路  如对于串 abcd 想要将其变为回文串
      那么先把它逆序 然后放在前面 自然是回文了 
                                   abcd
                                   dcba
                               dcbaabcd ->是回文
      但是我们发现根本没必要放这么多在前面 因为abcd的前缀和dcab的后缀有重合(如a) 所以为了只添加最少的字符,我们在前方只需要添加不重复的即可
                                    abcd
                                 dcba
                                 dcbabcd ->依然是回文
     //为了添加的最少 我们就需要找到dcba的后缀和abcd的前缀重合的部分，且让重合部分最大即可
     //故而联想到kmp算法，它的next数组就是用来求一个串的前缀和后缀相同的长度的最大值
     //所以拼接起字符串 abcddcba 但是我们所求的前缀是不能超过中点的，因此用一个特殊字符隔开
     //           即为 abcd#dcba 这样在匹配前后缀时，相同长度就一定不会超过#号了
     //           这样问题就转化为了 求abcd#dcba的next数组 易知该串的前后缀相同时的最大长度为1
                此时的最长相同前后缀即为a 和 a  
                                     所以把后半部分除去重叠的部分拼接到前半部分即可
                            答案就是  dcbabcd
                                     大功告成!
                  
     */
    string shortestPalindrome(string s) {
        string revs = s;//存s的逆序
        int tn = s.size();//中点处,#前面的位置
        reverse(revs.begin(),revs.end());
        s = ' '+ s + '#' + revs;//让下标从1开始
        int n = s.size()-1;//实际长度
        vector<int> ne(n+1);//next数组
        for(int i = 2, j = 0; i <= n; i++){//求next数组 
            while(j&&s[i]!=s[j+1]) j = ne[j];
            if(s[i]==s[j+1]) j++;
            ne[i] = j;
        }
        return s.substr(tn+2,tn-ne[n])+s.substr(1,tn);//后半部分除去重叠后缀+前半部分
    }