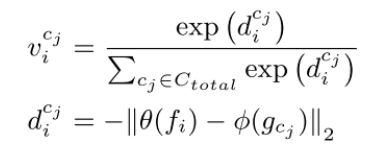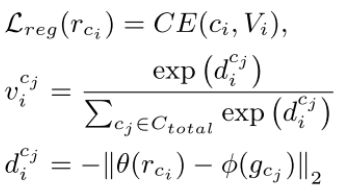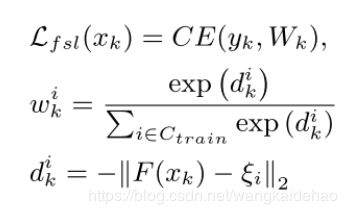Few-Shot Learning with Global Class Representations笔记整理

Few-Shot Learning with Global Class Representations笔记整理

1 Introduction

在小样本学习（Few-Shot Learning, FSL）问题上，对于base classes中的每个类别，我们往往有充足的训练数据；对于那些novel classes中的每个类别，我们只有少量的带标签的数据。FSL旨在利用base calsses中大量的数据，来学习出一个可以对novel classes中的数据标签准确辨别的模型。

注：base class和novel class是本文作者自己创造的词汇，我没有想到很好的翻译方法。在文章里，base class指拥有充足样本的类别（用于训练）；novel class指的是那些只有少量样本的类（用于测试）。

现在解决小样本学习问题一般都使用元学习的方法，但是元学习的做法也有一定的局限性，因为它们往往只使用了源数据（source data），但是对于目标数据却几乎没有使用，即使在经历过fine-tuning阶段，也无法保证能学习到满足目标数据需求的模型。（比如，要辨别一个动物是不是猫，但现在手头上只有5张猫的照片以及大量狗，狮子，鸟的照片。这个时候元学习的一般做法是先在狗，狮子和鸟的照片上进行训练，训练好后再用5张猫的照片来进行微调。）

而作者在本文提出的方法同时使用5张猫（novel classes）的照片和大量狗，狮子，鸟（base classes）的照片来进行训练，作者把这称为全局表征（global class representations）。

因为将novel class在的少量数据和base class中的大量数据一起训练的话，势必会有样本不平衡的问题，作者使用两种方法来解决这一问题：

• 合成novel class的新样本；
• 引入片段训练（episodic training）。

2 Contributions

1. 提出将base classes 和novel classes同时作为全局表征来进行小样本学习的训练；

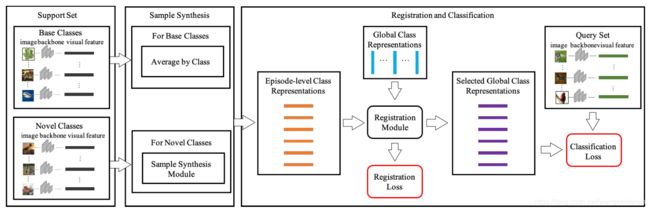
3 Method

在这一节将首先介绍本方法的两个模块：表征注册模块和样本合成模块。然后再介绍如何将这两个模块合并起来，最后介绍如何将此方法拓展到生成式FSL的设定中（generalized FSL）。其中使用$f_i=F(x_i)$表示一个样本$x_i$经过特征抽取器F之后得到的视觉特征。

Overview of the whole framework.

3.1 样本合成模块

本模块用于解决类别不平衡问题，共分为两步：第一步用原始样本生成新的样本，第二步用第一步获取的所有样本合成一个新样本。

首先对novel classes在的原始样本使用random cropping, random fipping和data hallucination操作(这三个方法出自论文：Low-shot learning from imaginary data.)来为每个novel class生成$k_t$个样本。

对于一个novel class$c_j$，作者先从中随机挑选出$k_r$个样本，具体操作如下：
$$\begin{gathered} \widehat{k_r}\sim U(0,k_t), \\ {k}_r=\lceil \widehat{k_r}\rceil \end{gathered}$$
其中，$U(a,b)$是平均分布。

对于一个novel class，再从$0\sim 1$平均分布中选出$k_r$个值$\{v_1,...,v_{k_r}\}$，将这$k_r$个值作为权重，对$k_r$个样本的视觉特征$\{f_1,...,f_{k_r}\}$求加权和。于是可以得到一个新的样本$r_{c_j}$，具体操作如下：
$$\begin{gathered} r_{c_j}=\sum _{i=1}^{k_r}\frac{v_i}{{\sum }_j{v}_j}{f}_i,where{y}_i=c_j \\ {v}_i\sim U(0,1) \end{gathered}$$
通过这种方法就可以扩大类内差异了，因此少量数据的问题就得到了缓解。

3.2 注册模块

给定全局类表征$G=\{g_{c_j},c_j\in C_{total}\}$和视觉特征$f_i$。我们将注册模块简记为R。针对每个视觉特征$f_i$，R将会生成一个N维向量$V_i=[v_i^{c_i},...,v_i^{c_N}{]}^T$，其中第$j$个元素是$f_i$和类别$c_j$的全局表征$g_{c_j}$之间的相似度分数。具体地：

其中,$\theta (.)$和$\varphi (.)$分别为样本的视觉特征和全局词表征的embeddings。

因此，我们可以设计一个注册损失$L_{reg}=CE(y_i,V_i)$，其中$y_i$为样本标签，CE为交叉熵损失。通过这个损失函数就可以使这个样本在embedding空间尽可能的靠近这个这个类的全局类表征。

通过将样本与其类别的全局表征在embedding空间进行比较，R模块可以使得该类的全局表征更靠近本类的样本，更疏远其他类的样本。（此处可以参考聚类的思想）

大致的流程可以参考下图：

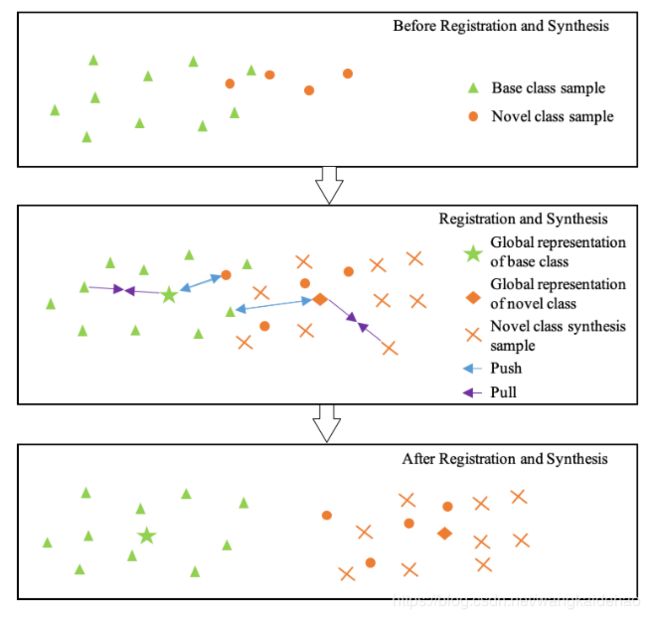
需要注意的是，图中的这些点都存在于embedding空间中。本方法的视觉特征$f_i$和全局类表征都是需要经过训练和优化的。训练好后会使用全局类表征向量取比对query集中的样本，从而确定它属于哪一类。

3.3 Few Shot Learning By Registration

$C_{total}$是所有类的结合，包括：base classes和novel classes。有人会好奇本文一开始的全局类表征是怎么得到的？其实很简单。我们可以通过对一类中所有样本的视觉特征$f_i$取平均来获得一个初始的全局类表征。本文模型的目标就是为每一个novel class学习出一个全局类表征。

除了使用数据合成策略来缓解数据不平衡问题，作者还引入了元学习中常用的片段学习策略。简而言之片段学习就是一次性采样多个类中一定数量的样本进行训练，这些类的集合就是所谓的片段或批量（episode/mimi-batch）。

但是novel class中的样本数量一般小于一个片段中所要求的样本数（$n_{support}+n_{query}$），比如进行5-way-5-shot实验，support样本数为5，query样本数为15，但是novel class只有5个样本。此时就需要使用样本合成模块对样本进行扩展了。

在进行片段学习时，我们首先将采样出的图片输入特征抽取器$F$，从而生成相应的视觉特征。然后我们依据采样出的support set中的数据为每一类构造出相应的片段表征$\{r_{c_i},c_i\in C_{train}\}$。需要注意的是这里的片段表征是一种局部表征（相对于全局表征）。

对于base classes，我们只需对每个类中样本的视觉特征$f_i$取平均就可得到片段表征；对于novel classes，我们需要利用样本合成模块来为每类合成一个新样本，这个新样本就是这个novel class的片段表征。

然后我们将片段表征（基于一个episode的样本）和全局表征（基于全部样本）输入注册模块R，从而计算出他们的相似度。类似的作者定义了一个片段表征$r_{c_i}$的损失函数：

其中$V_i=[v_i^{c_1},...,v_i^{c_N}{]}^T$表示片段表征$\{r_{c_i},c_i\in C_{train}\}$和所有全局表征$\{g_{c_j},c_j\in C_{total}\}$之间的相似度。

我们将依据这里的相似度来选择全局类表征，并依据全局表征通过最近邻法来对query数据集中的样本进行分类。相似地，分类损失的计算方法为：

其中$W_k=[w_k^1,...,w_k^{n_{train}}{]}^T$指的是选择出的（用argmax方法进行选择）全局表征${\xi }_i$和query样本$x_k$之间的相似度。

将注册损失和分类损失进行合并在一起就得到了最终的损失函数：

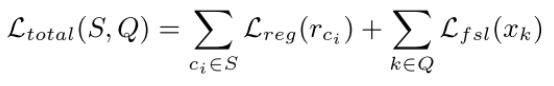
我们将依据这个损失函数来更新全局表征，注册模块中的参数和特征抽取器中的参数。

4 实验和讨论

模型架构

特征抽取器$F$：4个卷积块，每个卷积块包含64个$3\times 3$的卷积层，1个batch normalization层，一个ReLU层和一个$2\times 2$的最大池化层。

5 结论

本文提出了一种利用全局类表征来解决小样本学习问题的方法，同时此方法可以轻易地拓展到生成式小样本学习中。