从word2vec到node2vec
word2vec
1. 什么是word2vec
在自然语言处理任务(NLP)中,最细粒度是词语,所以处理NLP问题,首先要处理好词语。
由于所有自然语言中的词语,都是人类的抽象总结,是符号形式的。而对于数学模型,如果要建立词语到词性关系的映射,必须使用数值形式的输入。因此,需要把他们都嵌入到一个数学空间中,就叫词嵌入(word embedding),而word2vec就是词嵌入的一种。
大部分有监督机器学习模型都可以归结为:
f(x) -> y
在NLP中,把x看作一个句子里的一个词语,y是这个词语的上下文词语,那么这里的f,便是NLP中经常出现的『语言模型』(language model)。这个模型的目的,便是判断(x,y)这个样本是否符合自然语言的法则。
word2vec便是来源于这种思想,但是它最终的目的不在于把f训练的完美,而是关心模型输出的模型参数,是否能够完整地向量化整个句子。
2. Skip-gram和CBOW模型
对于上面提到的语言模型
- 如果是用一个词语作为输入,预测其上下文,这个模型叫做『Skip-gram』模型。
- 如果是拿一个词语的上下文作为输入,预测这个词语本身,则是『CBOW』模型。
2.1. Skip-gram和CBOW的简单情形
一个例子。y是x的上下文,当y只取上下文中的一个词语时,语言模型变成:
用当前词x预测它的下一个词y
但这时输入显然不能使x本身,也不能是word2vec,因为这是训练后的产物。对于初始阶段,我们想要的是x的一个原始输入形式,这时我们就会采用one-hot encoder。
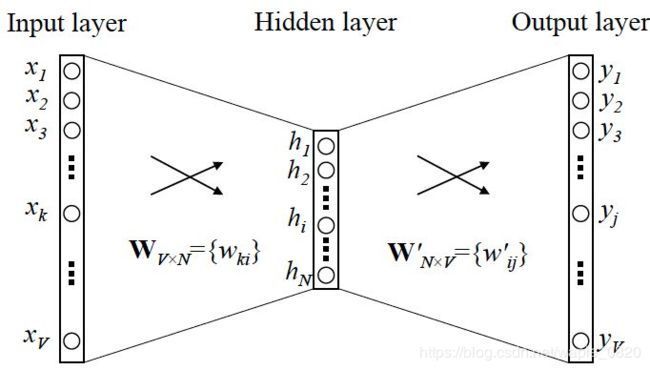
对于skip-gram网络结构,如图1所示,x就是上面提到的one-hot encoder形式的输入,y是在这v个词上输出的概率,我们希望真实的y的one-hot encoder一样。
在这个网络中,隐层的激活函数其实是线性的。如果要训练这个模型,用反向传播算法本质上其实是链式求导。
当模型训练完了之后,最后得到的是神经网络的权重。比如一个特定词语它的one-hot encoder:[1,0,0,…,0],则在输入层到隐含层的权重里,只有对应1这个位置的权重被激活,这些权重的个数,跟隐含层节点数是一致的,从而这些向量vx来表示x,并且又因为每个词语的one-hot表示方法都不同,所以vx也可以用来唯一地表示x。
对于输入向量和输出向量,我们一般使用『输入向量』作为压缩后的词向量。需要注意的是,一般情况下词向量的维度远远小于词语总数的大小,所以word2vec本质上是一种降维操作。
2.2. Skip-gram更一般情形
当x只有一个词,y有多个词时,网络结构如下:

图2. skip-gram的一般结构
这种情况下可以看成是单个x到单个y模型的并联,本质上是cost function变成了所有单个cost function的累加(取log之后)。
2.3. CBOW更一般的情形
与Skip-gram的类似,只不过Skip-gram是预测一个词的上下文,而CBOW是用上下文预测这个词。

图3. CBOW的一般结构
这里输入变成了多个单词,所以对输入需要进行处理,一般是求和后平均,输出的cost function不变。
3. word2vec训练tricks
hierarchical softmax
用霍夫曼树的结构解决了softmax计算量大的问题,本质是将N分类变成了log(N)次的二分类。
negative sampling
- 在模型中将共同出现的单词对或者短语当做单个词。
- 二次采样经常出现的单词,以减少数据的数量。
- 将会使训练样本更新少量模型的weights。
本质是预测总体类别的一个子集。并且对频繁词进行二次抽样和应用负抽样不仅减少了训练过程的计算负担,而且还提高了结果词向量的质量。
4. Reference
- Gensim:官网 & 教程
- word2vec的数学原理详解: 链接
- Python interface to Google word2vec: github
- word2vec本质的解释:知乎
node2vec
1. 论文地址
名称:node2vec: Scalable Feature Learning for Networks
node2vec: 原文链接
2. 与word2vec关联
前文提到的word2vec任务主要是将人类语言符号转化为可输入到模型的数学符号。与之类似类似,拥有网络结构数据的图,通常也无法直接输入到模型中进行计算,这就需要我们用相类似的方法,将一个图所包含的信息尽可能的用向量表示。
图数据其实非常常见,例如社交网络关系、分子结构、论文相互引用的关系网络等等,所以如何表达网络节点的特征就十分重要。表达好了节点的特征,我们就可以用它来做下游的分类、预测、聚类、可视化等等的任务。
3. 传统的图特征表示方法
既然需要处理图数据,那么就必须首先通过合适的方法将图的重要特征提取出来。在node2vec之前,主要还是选用一些基础的方法。
3.1 特征工程
处理图数据,直接请专家人工定义网络节点的特征,这其中涉及到许多图论的知识和领域知识。
优点:
- 这种特征工程方法往往最后可以在特定的任务上取得比较好的效果。
缺点:
- 泛化性能差。效果好往往仅针对单一任务。
- 需要耗费巨大的人力无力。(主要问题)
- 人工判断出现偏差的可能较大。
3.2 在任务中学特征
通过定义一个下游任务,将这些特征作为参数,通过大量数据去学。
这种方法解决了3.1中人力开销的问题,但是大量的数据又带来了很大的计算开销。并且同样是也监督学习,泛化能力就会大打折扣。
3.3 隐模型法/降维/矩阵分解法
这类方法总体思想和推荐系统中的矩阵分解法十分类似,属于无监督学习。该方法尝试将原来的网络结构表达成一个巨大的稀疏矩阵,然后通过Factorization来得到隐表示,作为各个节点的表示向量。这一类方法主要问题同样在于计算的开销过大,另外,很多实证表明这样的方法效果并不好。
4. 本文方法
首先word2vec方法从大量无标注文本中学得词语的分布式表示,不仅蕴含了大量的信息,而且可以迁移到各种下游任务中。同样,在网络中也存在很多很多通路,将各个节点连成一条线,这些连线同样也蕴含着节点之间的相互关系,就如同句子中各个词语的关系一样。
因此,本文的作者尝试将这些节点序列当做句子,用word2vec方法进行训练,就能够得到比较好的node的向量表示了。
那么现在的问题就变成了:如何生成有效的Node序列。
4.1 如何生成node sequence
论文中给出了一个图来辅助说明:

上图中可以明显看到有两个小团体,分别以u和s6为中心。如果这就是一个简单的社交网络关系,可以猜测u与s1,s2,s3,s4及s6与s5,s7,s8,s9都是同班同学的关系,但是两者并不属于同一个班。其中u和s6可能是两个班长(与所有人都保持联系)。
接下来需要定义生成节点序列的规则。
首先需要确定的是,多个节点放入到同一个序列中,说明你认为他们在某种意义上是相似的。这种相似可以是网络中直接的邻居(这种情况称为homophily),也可以是结构上的相似,如互为班长的u和s6(structural equivalence)。
要想从一个节点去寻找它的直接邻居,需要通过BFS的方法去搜(如上图红色箭头),而如果想要尽快找到结构相似的,就需要通过DFS的方法去搜(如上图蓝色箭头)。
node2vec使用的方法:
biased random walk
在网络的表示中,位置相似(邻居点)和结构相似都很重要,我们希望在生成随机序列的时候可以同时考虑这两种相似性。
并且,我们希望可以有参数控制一个偏重,在不同的任务中可以随时调整这个参数达到泛化的效果。针对这一想法作者给出了下图:
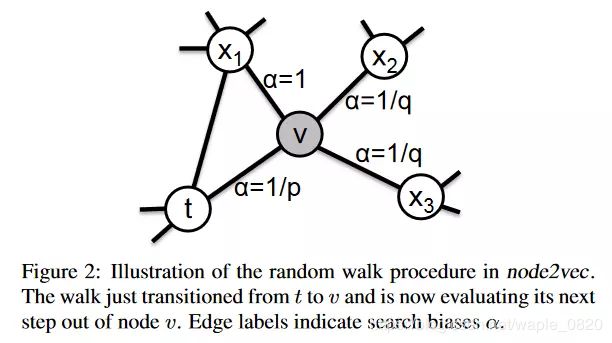
上图是作者对node2vec中随机游走策略的一个解释。假设从t节点开始一个random walk,现在到达了v节点。如果采取BFS策略的话,应该走到x1,因为v和x1都是t节点的直接邻居,如果采取DFS策略的话,应该走向x2或x3,因为它们和t都中间隔了一步。当然也可能又返回到t节点。
于是作者设计了一个二阶转移概率算法:
两个节点之间的转移概率为:
π v x = α p q ( t , x ) ⋅ ω v x \pi_{vx}=\alpha_{pq}(t,x)\cdot\omega_{vx} πvx=αpq(t,x)⋅ωvx
其中w为这两个节点之间边的权重,这个权重根据实际的场景而定,而 α \alpha α为search bias,定义为:
α p q ( t , x ) = { 1 p i f d t x = 0 1 i f d t x = 1 1 q i f d t x = 2 \alpha_{pq}(t,x) = \left\{ \begin{aligned} \frac{1}{p} \quad if \quad d_{tx}=0 \\ 1 \quad if \quad d_{tx}=1 \\ \frac{1}{q} \quad if \quad d_{tx}=2 \end{aligned} \right. αpq(t,x)=⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧p1ifdtx=01ifdtx=1q1ifdtx=2
这也就是说,一个节点的下一步应该怎么走,取决于它的上一步和下一步的关系。
对这个公式解释一下:v是当前节点,t是v上一步所在的节点,而x代表下一步的位置。
d(t,x)代表t和x之间的最短距离:
- 当d=0时,就是从v又回到t节点的意思,这个时候search bias为1/p,可以理解为以1/p的概率返回上一步;
- 当d=1时,则x为t的直接邻居,相当于BFS,这时的bias为1;
- 当d=2时,x是t邻居的邻居,相当于dfs,这时bias为1/q
作者称p为return parameter,因为p控制回到原节点的概率;称q为in-out parameter,因为这个参数控制着BFS和DFS的关系。
这样,当我们设置不同的p和q时,就可以得到不一样偏重的node sequence。在训练模型的时候,可以使用grid search来寻找最优的p和q。也可以根据场景需求来自行确定p和q。
4.3 如何学习节点特征
这里就是完全借鉴word2vec的方法。
总的目标函数是:
max f ∑ u ∈ V log P r ( N S ( u ) ∣ f ( u ) ) . \max \limits_{f} \sum_{u \in V} \log Pr(N_{S}(u)|f(u)). fmaxu∈V∑logPr(NS(u)∣f(u)).
这里的f就是把节点u映射到特征空间的函数,N(u)是通过前面的node sequence得到的u的近邻节点,相当于上下文。
具体计算:
P r ( N S ( u ) ∣ f ( u ) ) = ∏ n i ∈ N S ( u ) P r ( n i ∣ f ( u ) ) . Pr(N_{S}(u)|f(u)) = \prod_{n_{i} \in N_{S}(u)}Pr(n_{i}|f(u)). Pr(NS(u)∣f(u))=ni∈NS(u)∏Pr(ni∣f(u)).
P r ( n i ∣ f ( u ) ) = e x p ( f ( n i ) ⋅ f ( u ) ) ∑ u ∈ V e x p ( f ( v ) ⋅ f ( u ) ) . Pr(n_{i}|f(u)) = \frac{exp(f(n_{i})\cdot f(u))}{\sum_{u \in V} exp(f(v) \cdot f(u))} . Pr(ni∣f(u))=∑u∈Vexp(f(v)⋅f(u))exp(f(ni)⋅f(u)).
与前文中提到的word2vec的方法一致。
4.4 node2vec算法框架
4.5 如何表示边的特征
对于点的特征上面已经学习到了,但是在图中,很多任务是针对边的,因此对图嵌入我们也需要边的特征。
作者提到,一条边实际上就是由两个节点决定的,因此可以用两个节点的特征来表示,作者给出了一些可选选项:

5. 可视化
作者在一个任务关系网络上尝试了node2vec,通过kmeans聚类,并做了一个可视化,看看node2vec得到的节点向量反映出网络的什么特点。
p=1, q=0.5的效果:
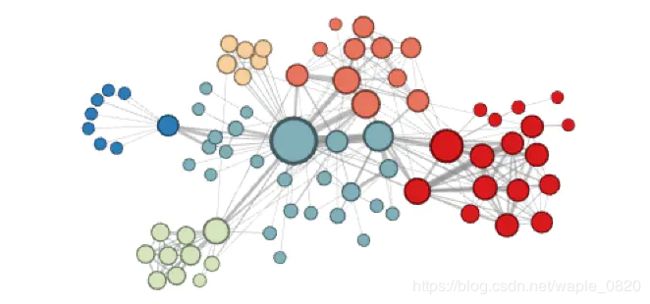
可以看出这个时候各个小区、小团体被聚为一类。
p=1, q=2的效果:

这个时候,可以发现各个社区之间的桥梁蓝色节点被聚成一类,因为他们有类似的结构特点,而淡黄色的点,是属于人物关系中比较边缘化的人。
对于节点分类和链路预测的结果就不作过多赘述。
6. 现成资源
斯坦福官网:链接
7. Reference
- 简书博客
- 知乎论文笔记