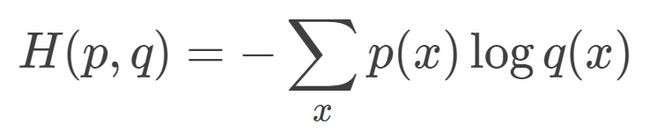交叉熵
分类问题中，预测结果是（或可以转化成）输入样本属于n个不同分类的对应概率。比如对于一个4分类问题，期望输出应该为 g0=[0,1,0,0] ，实际输出为 g1=[0.2,0.4,0.4,0] ，计算g1与g0之间的差异所使用的方法，就是损失函数，分类问题中常用损失函数是交叉熵。
交叉熵（cross entropy）描述的是两个概率分布之间的距离，距离越小表示这两个概率越相近，越大表示两个概率差异越大。对于两个概率分布 p 和 q ，使用 q 来表示 p 的交叉熵为：
神经网络的输出，也就是前向传播的输出可以通过Softmax回归变成概率分布，之后就可以使用交叉熵函数计算损失了。
交叉熵一般会跟Softmax一起使用，在tf中对这两个函数做了封装，就是 tf.nn.softmax_cross_entropy_with_logits 函数，可以直接计算神经网络的交叉熵损失。
cross_entropy = tf.nn.softmax_cross_entropy_with_logits(y, y_)其中 y 是网络的输出，y_ 是期望输出。
针对分类任务中，正确答案往往只有一个的情况，tf提供了更加高效的 tf.nn.sparse_softmax_cross_entropy_with_logits 函数来求交叉熵损失。
均方误差
与分类任务对应的是回归问题，回归问题的任务是预测一个具体的数值，例如雨量预测、股价预测等。回归问题的网络输出一般只有一个节点，这个节点就是预测值。这种情况下就不方便使用交叉熵函数求损失函数了。
回归问题中常用的损失函数式均方误差(MSE,mean squared error)，定义如下：
均方误差的含义是求一个batch中n个样本的n个输出与期望输出的差的平方的平均值。
tf中实现均方误差的函数为：
mse = tf.reduce_mean(tf.square(y_ - y))在有些特定场合，需要根据情况自定义损失函数，例如对于非常重要场所的安检工作，把一个正常物品错识别为危险品和把一个危险品错识别为正常品的损失显然是不一样的，宁可错判成危险品，不能漏判一个危险品，所以就要在定义损失函数的时候就要区别对待，对漏判加一个较大的比例系数。在tf中可以通过以下函数自定义：
loss = tf.reduce_sum(tf.select(tf.greater(v1,v2),loss1,loss2))