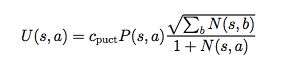接上文继续学习蒙特卡洛树搜索MCTS和深度神经网络相互应用转化关系。
除上文提到的3位作者文章外,由于不理解下面公式提到的“双方向镜面和旋转”,通过文章搜索找到一篇类似解读文章,所配图片看明白了此概念,在说明蒙特卡洛树搜索算法的Expand树时会放上。
接下来展开说明蒙特卡洛树搜索算法:
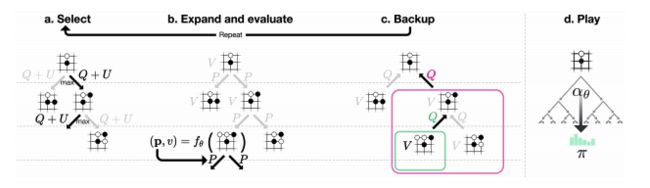
按照论文所述,每次MCTS使用1600次模拟。过程大概是自己跟自己下棋,每下一步棋,都要通过MCTS模拟1600次上图中的a~c,从而得出我这次要怎么走子。来说说a~c,MCTS类似一棵树,这棵树的每个节点保存了每一个局面(situation),并包含一条边对应所有可能走子(action)的信息。这条边信息分别是:N(s, a)是访问次数,W(s, a)是总行动价值,Q(s, a)是平均行动价值,P(s, a)是被选择的概率。
a.Select:Select每次模拟的过程都一样,从父节点的局面开始,选择一个走子。比如开局的时候,所有合法的走子都是可能的选择,那么我该选哪个走子呢?这就是select要做的事情。MCTS选择Q(s, a) + U(s, a)最大的那个action,U的公式如下:
通过Q+U计算就知道当前局面下,哪个action的Q+U值最大,那这个action走子之后的局面就是第二次模拟的当前局面。比如开局,Q+U最大的是第3步,然后就Select第3步这个action,再下一次Select就从第3步的这个棋局选择下一个走子。
b. Expand:现在开始第二次模拟,假如之前的action是第3步,我们要接着这个局面选择action,但是这个局面是个叶子节点。就是说第3步之后可以选择哪些action不知道,这样就需要expand了,通过expand得到一系列可能的action节点。这样实际上就是在扩展这棵树,从只有根节点开始,一点一点的扩展。
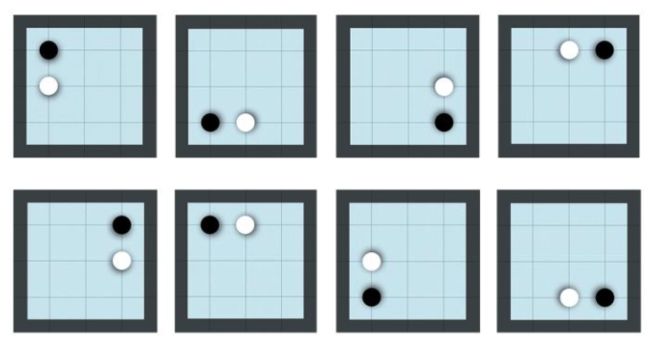
将叶子节点 sL(这里的L指第3步)加到队列中等待输入至神经网络进行评估, fθ(di(sL))=(di(p),v),其中 di表示一个1至8的随机数来表示双方向镜面和旋转(从8个不同的方向进行评估,如下图所示,围棋棋型在很多情况如果从视觉角度来提取特征来说是同一个节点,极大的缩小了搜索空间)。
队列中8个不同位置组成一个大小为8的mini-batch输入到神经网络中进行评估。整个MCTS搜索线程被锁死直到评估过程完成(这个锁死是保证并行运算间同步)。叶子节点被展开(Expand),每一条边 (sL,a)被初始化为:N(sL,a)=0;W(sL,a)=0;Q(sL,a)=0;P(sL,a)=Pa。这里的Pa由将 s输入神经网络得出 P(包括所有落子可能的概率值 Pa),然后将神经网络的输出值 v传回(backed up)。
c. Backup:边的统计数据在每一步t≤L中反向更新。
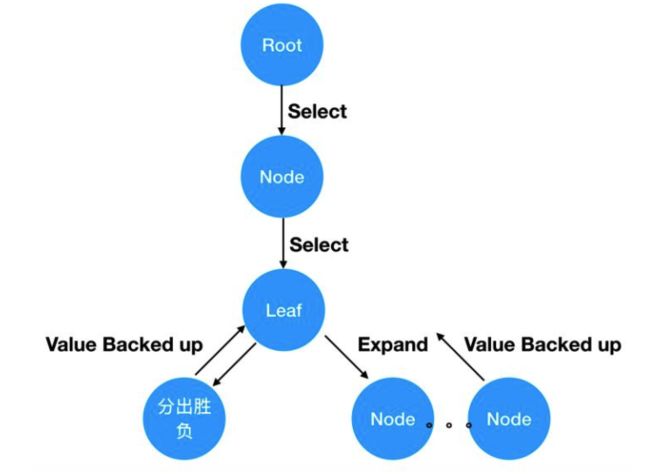
使用虚拟损失来确保每个线程评估不同的节点。任意一个局面(就是节点),要么被展开过(expand),要么没有展开过(就是叶子节点)。展开过的节点可以使用Select选择动作进入下一个局面,下一个局面仍然是这个过程,如果展开过还是可以通过Select进入下下个局面,这个过程一直持续下去直到这盘棋分出胜平负了,或者遇到某个局面没有被展开过为止。如果没有展开过,那么执行expand操作,通过神经网络得到每个动作的概率和胜率v,把这些动作添加到树上,最后把胜率v回传(backed up)。
backed up给谁?这是一路递归下去的过程,一直在Select,递归必须要有结束条件,不然就是死循环。所以分出胜负和遇到叶子节点就是递归结束条件,把胜率v或者分出的胜平负value作为返回值,回传给上一层。这个过程就是evaluate,是为了Backup步骤做准备。因为在Backup步骤,要用v来更新W和Q的,但是如果只做了一次Select,棋局还没有结束,此时的v是不明确的,必须要等到一盘棋完整的下完才能知道v到底是多少。就是说现在下了一步棋,不管这步棋是好棋还是臭棋,只有下完整盘期分出胜负,才能给下的这步棋评分。不管这步棋的得失,即使这步棋局面处于劣势,但最后赢了,那这个v就是积极的。同样即使这步棋处于优势局面,但最后输棋了,也不能认为我这步棋就是好棋。
当值被回传,就要做Backup了,这里很关键。因为是多线程同时在做MCTS,由于Select算法都一样,都是选择Q+U最大节点,所以很有可能所有的线程最终选择的是同一个节点,这就尴尬了。目的是尽可能在树上搜索出各种不同的着法,最终选择一步好棋,怎么办呢?论文中已经给出了办法,“使用虚拟损失来确保每个线程评估不同的节点。”就是说,通过Select选出某节点后,人为增大这个节点的访问次数N,并减少节点的总行动价值W,因为平均行动价值Q = W / N,这样分子减少,分母增加,就减少了Q值,这样递归进行的时候,此节点的Q+U不是最大,避免被选中,让其他的线程尝试选择别的节点进行树搜索。这个人为增加和减少的量就是虚拟损失virtual loss。
现在MCTS的过程越来越清晰了,Select选择节点,选择后,对当前节点使用虚拟损失,通过递归继续Select,直到分出胜负或Expand节点,得到返回值value。现在就可以使用value进行Backup了,但首先要还原W和N,之前N增加了虚拟损失,这次要减回去,之前减少了虚拟损失的W也要加回来。
然后开始做Backup,“边的统计数据在每一步t≤L中反向更新。访问计数递增和动作价值更新为平均值”,同时我们还要更新U。这个反向更新就是递归的把值返回回去。有一点一定要注意,就是我们的返回值一定要符号反转,就是说对于当前节点是胜,那么对于上一个节点一定是负,所以返回的是-value。
d. play:按照上述过程执行a~c,论文中是每步棋执行1600次模拟,那就是1600次的a~c,这个MCTS的过程就是模拟自我对弈的过程。模拟结束后,基本上能覆盖大多数的棋局和着法,每步棋该怎么下,下完以后胜率是多少,得到什么样的局面都能在树上找到。然后从树上选择当前局面应该下哪一步棋,这就是步骤d.play:在搜索结束时,AlphaGo Zero在根节点s0选择一个走子a,与其访问计数幂指数成正比,在随后的时间步重新使用搜索树:与所走子的动作对应的子节点成为新的根节点;保留这个节点下面的子树所有的统计信息,而树的其余部分被丢弃。如果根节点的价值和最好的子节点价值低于阈值v_resign,则AlphaGo Zero会认输。
当模拟结束后,对于当前局面(就是树的根节点)的所有子节点就是每一步对应的action节点,选择哪一个action呢?按照论文所说是通过访问计数N来确定的。当前节点的所有节点是可以获得的,每个子节点的信息N都可以获得,然后从多个action中选一个,这其实是多分类问题。使用softmax来得到选择某个action的概率,传给softmax的是每个action的logits(N(s_0,a) ^(1/τ)),这其实可以改成1/τ * log(N(s_0,a))。这样就得到了当前局面所有可选action的概率向量,最终选择概率最大的那个action作为要下的一步棋,并且将这个选择的节点作为树的根节点。按照前图中a.Self-Play(《AlphaGo Zero学习二》中Self-play reinforcement learning in AlphaGo Zero图示)的表述就是从局面s_t进行自我对弈的树搜索(模拟),得到a_t∼ π_t,a_t就是动作action,π_t就是所有动作的概率向量。最终在局面s_T的时候得到胜平负的结果z,就是我们上面所说的value,至此MCTS算法就分析完了。
神经网络补充说明:
神经网络在《AlphaGo Zero学习二》说过,通过MCTS算出该下哪一步棋。然后接着再经过1600次模拟算出下一步棋,如此循环直到分出胜负,这样一整盘棋就下完了,这就是一次完整的自对弈过程,那么MCTS就相当于人在大脑中思考。把每步棋的局面s_t 、算出的action概率向量 π_t 和胜率z_t (就是返回值value)保存下来,作为棋谱数据训练神经网络。神经网络的输入是局面s,输出是预测的action概率向量p和胜率v,训练目标是最小化预测胜率v和自我对弈的胜率z之间的误差,并使神经网络走子概率p与搜索概率π的相似度最大化。按照论文中所说,具体而言,参数θ通过梯度下降分别在均方误差和交叉熵损失之和上的损失函数l进行调整,就是让神经网络的预测跟MCTS的搜索结果尽量接近。
胜率是回归问题,优化用MSE损失,概率向量的优化要用softmax交叉熵损失,目标就是最小化这个联合损失。(此部分结论待深入实践CNN后实施验证)