scikit-learn机器学习（三）--逻辑回归和线性判别分析LDA

scikit-learn机器学习（一）–多元线性回归模型
scikit-learn机器学习（二）–岭回归，Lasso回归和ElasticNet回归
scikit-learn机器学习（三）–逻辑回归和线性判别分析LDA

前面的线性回归模型是解决预测问题的，根据样本的多个特征，推测其目标值，但是现实生活中除了这种预测问题之外，还有一种问题就是分类问题，比如这个人是否得病，邮件是否为垃圾邮件等

逻辑回归和LDA就用于这一类的分类问题

一丶逻辑回归

逻辑回归虽然名字是回归，实际上他是一个分类模型，一般的线性模型他的值是连续的，而我们把这种线性模型进行映射，使其值不连续（比如0或者1），帮助我们进行分类判断

它的核心思想是：如果回归的结果输出是一个连续值，而值的范围是无法限定的，那么想办法把这个连续结果值映射为可以帮助我们判断的结果值，从而进行分类。所以，从本质上讲，逻辑回归是在回归的基础上，进行了特殊的改进，而被用于分类问题上。

（1）模型

广义线性回归模型：
身体健康指数与身高，体重，年龄和体脂有关系，另其分别为：x1,x2,x3,x4,则其线性模型公式为：

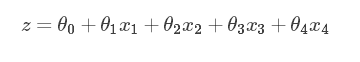
逻辑回归模型是对上面的线性模型进行映射，这个映射将样本的值转化为概率，使其能进行分类，因此引入sigmoid函数进行映射，公式如下：

其函数表象为：

因此通过这个sigmoid映射函数，上述线性模型构造为逻辑回归模型，公式为：

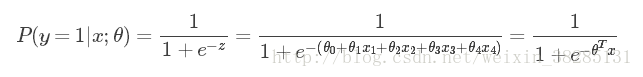
（2）损失函数

常见的损失函数有0-1损失函数，平方和损失函数，绝对值损失函数，对数损失函数或者对数似然损失函数

逻辑回归模型所采用的对数似然损失函数公式为：

由此，逻辑回归损失函数为：

将上述公式合并，可获得单个点的损失函数：

此时y只能取值为0或者1，与上述分段式函数结果相同
将上述公式扩展到所有样本，可得：

最终逻辑回归损失模型为：

（3）Python实现
scikit-learn机器学习库中LogisticRegression实现了逻辑回归模型，其中封装了逻辑回归损失函数的最优解求解方法，包括牛顿法，L-BFGS拟牛顿法，libinear法和随机梯度下降法
注：
liblinear规模较小的数据，梯度下降法适用于规模大的数据集

利用scikit-learn中的鸢尾花数据集进行分类测试
代码：

from sklearn import datasets,linear_model,discriminant_analysis
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split

def load_data_iris():#加载鸢尾花数据
    iris=datasets.load_iris()
    x_train=iris.data
    y_train=iris.target
    return train_test_split(x_train,y_train,test_size=0.25,random_state=0,stratify=y_train)

def test_LogisticRegression(*data):
    x_train,x_test,y_train,y_test=data
    regr=linear_model.LogisticRegression()#逻辑回归模型
    regr.fit(x_train,y_train)#数据训练
    print('Coefficients:%s,intercept %s' % (regr.coef_, regr.intercept_))#权重和截距
    print('Score:%.2f' % regr.score(x_test, y_test))

x_train,x_test,y_train,y_test=load_data_iris()
test_LogisticRegression(x_train,x_test,y_train,y_test)

结果如下：

准确率为97%

scikit-learn逻辑回归模型参数：
penalty：正则化策略
solver：求解最优化策略，牛顿法，拟牛顿法，liblinear，sag等
multi_class:多分类策略，包括ovr（默认），multinomial：直接采用多分类回归策略只有在用牛顿法或者拟牛顿法时才能用

改变下列参数，也可以提高精度，可以试一下。

multi_class对其影响：

regr = linear_model.LogisticRegression(solver='lbfgs',multi_class='multinomial')#修改solver和多分类策略

结果：

可以看到精度提高，也可以修改正则化策略，这里就不写出来了

二丶线性判别分析（LDA）

LDA基本思想：

训练：
设法将训练样本投影到一条直线上，使同类样本投影点尽可能的接近，异类样本的投影点尽可能的原理，需要训练出这样一条直线
预测分类：
将待预测样本投影到学到的直线上，根据投影的位置来判断类别

如图所示：

如上两幅图所示，第二幅图即为我们要求的直线，将两个样本完全分开，LDA选择分类性能最好的方向

python代码：

def load_data_iris():
    iris=datasets.load_iris()
    x_train=iris.data
    y_train=iris.target
    return train_test_split(x_train,y_train,test_size=0.25,random_state=0,stratify=y_train)
def test_LDA(*data):
    x_train, x_test, y_train, y_test = data
    lda=discriminant_analysis.LinearDiscriminantAnalysis()
    #regr = linear_model.LogisticRegression(solver='lbfgs', multi_class='multinomial')
    lda.fit(x_train, y_train)
    print('Coefficients:%s,intercept %s' % (lda.coef_, lda.intercept_))
    print('Score:%.2f' % lda.score(x_test, y_test))
x_train,x_test,y_train,y_test=load_data_iris()
test_LDA(x_train,x_test,y_train,y_test)

结果如下：

分类精度为1，完全正确

我们将分类结果画出来

def plot_LDA(convert_x,y):
    from mpl_toolkits.mplot3d import Axes3D
    fig=plt.figure()
    ax=Axes3D(fig)
    colors='rgb'
    markers='o*s'
    for target,color,marker in zip([0,1,2],colors,markers):
        pos=(y==target).ravel()
        x=convert_x[pos,:]
        ax.scatter(x[:,0],x[:,1],x[:,2],color=color,marker=marker,label='Label%d'%target)
    ax.legend(loc='best')
    fig.suptitle('Iris after LDA')
    plt.show()
x_train, x_test, y_train, y_test = load_data_iris()
x=np.vstack((x_train,x_test))
y=np.vstack((y_train.reshape(y_train.size,1),y_test.reshape(y_test.size,1)))
lda=discriminant_analysis.LinearDiscriminantAnalysis()
lda.fit(x,y)
convert_x=np.dot(x,np.transpose(lda.coef_))+lda.intercept_
plot_LDA(convert_x,y)

结果如图：

参考：
https://blog.csdn.net/saltriver/article/details/63681339
《python大战机器学习》