【吴恩达机器学习笔记】Week5 ex4 nnCostFunction part1 答案

被Week5的ex4中nnCostFunction的part1卡了一下，现在弄懂了，说一下自己的理解

% Part 1: Feedforward the neural network and return the cost in the
%         variable J. After implementing Part 1, you can verify that your
%         cost function computation is correct by verifying the cost
%         computed in ex4.m

m_1 = size(X,1);
X = [ones(m_1, 1) X];
z_2 = X* Theta1';
a_2 = sigmoid(z_2);

m_2 = size(a_2, 1);
a_2 = [ones(m_2,1) a_2];
z_3 = a_2* Theta2';
a_3 = sigmoid(z_3);
h = a_3;

com_label = [1:num_labels];   
y_i = y==com_label;
J = (1/m)* sum(sum(((-y_i) .* log(h) - (1 - y_i) .* log(1 - h))));
%或者下面也可以
%J = (1/m)* sum(diag(((-y_i)'* log(h) - (1 - y_i)'* log(1 - h))));

写出正确的J有两个关键，一是理解J的实际计算过程，二是注意矩阵乘法的陷阱

1. J的计算过程

（1）当为label只有一个的情况下，即为二分类任务时，网络的输出层是1个神经元（或者两个也可以）当为label只有一个的情况下，即为二分类任务时，网络的输出层是1个神经元（或者两个也可以）

h即为神经网络计算出的值（此时h为0到1之间的一个数），与y进行比较（此时y为0或1）
即h为模型的预测值，我们想要做到的就是使得h尽可能的接近实际的y值（注意：h只能在0和1之间变化）

（2）当label为3个或者3个以上时，从我们人类的角度看，label为1，2，3……10，但是对于算法而言，sigmoid函数输出范围是[0，1]，若y的值（即label的值）用大于1的数来表示的话，h永远也无法超过1，而且，对于每一个样本，神经网络输出的维数等于label的个数，所以对于y也不能只有一个数字表示

下面这个例子是针对一个样本而言！
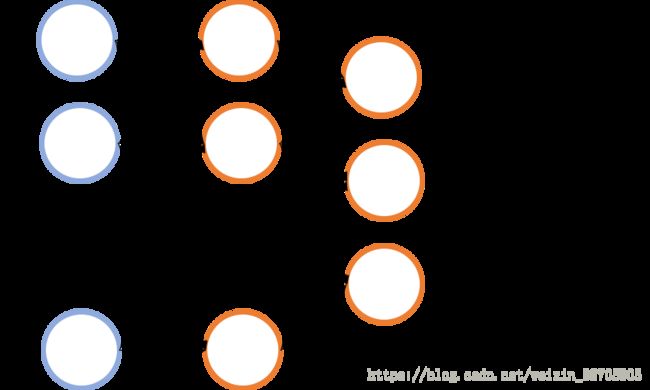
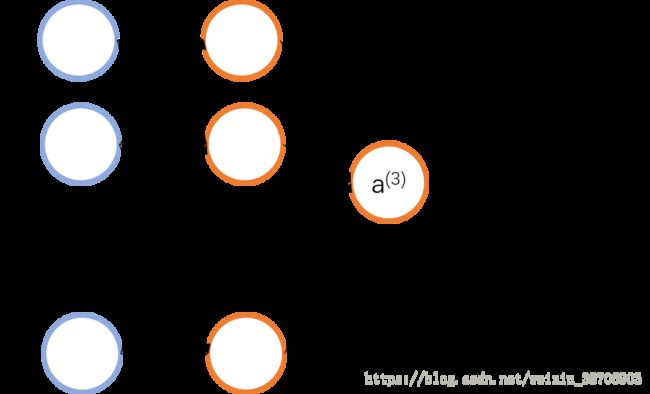
例如在下图，一个输出层为3个神经元的神经网络，h在神经网络中输出为一个3维的列向量，例如h=[0.2， 0.5， 0.9]’，当实际label为3即y=3时，此时y的维度是1，h的维度是3，h所代表的是每一个label可能的概率，因此，想要将y和h关联起来，y的维度也要发生变化，所以y要变成[0，0，1]’

换一个角度，实际上可以单独看h的一行看成是1次二分类的结果（也就是图1），将h和y的同一行看成一个整体，看成是1次二分类

例子中，h有三行，所以是进行了三次二分类，也就是说，第一次二分类的实际label为0，h的预测值为0.2，第二次二分类的实际label为0，h的预测值为0.5，第三次二分类的实际label为1，h的预测值为0.9，我们要做的任务和以前一样，就是使得每一次二分类的预测值与实际值尽可能地接近，这样就使得了多分类任务和二分类任务本质和计算过程都是一样的，只不过是输出的维度发生了变法（输出层的神经元个数）

下面开始说J，在J的公式中，K代表了label的种类个数

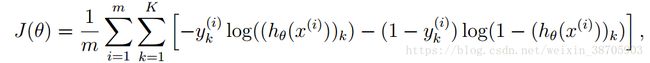
我们不妨将K当成1，这样得到的是二分类时候的J，J的含义是cost funciotn，是衡量模型是否贴合实际情况的一个性能指标，J越小越好
右边中括号里面的东西计算的是针对单个样本，研究预测值h与实际值y的关系 （在后文中，中括号里面的那一串运算都用“研究关系”来指代），同样也是越小，说明预测的越准确

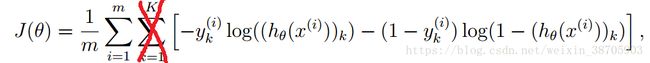
举个列子，当为二分类任务，样本为4个时，y和h的情况可能想下图一样，按照公式计算J=0.1643
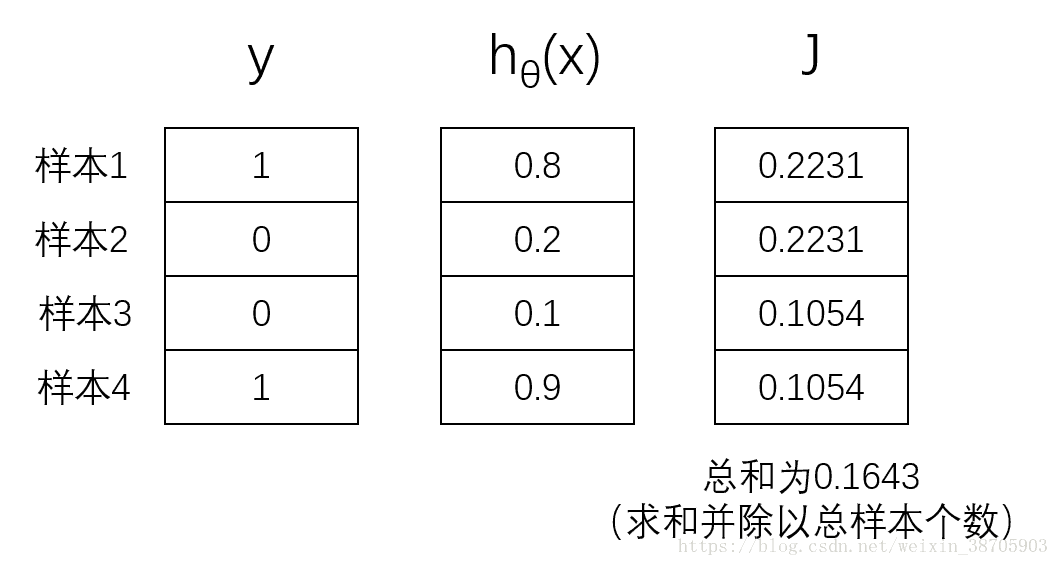实际代码为

y = [1 0 0 1]';
h = [0.8 0.2 0.1 0.9]';
m=4;
J = sum((-y).*log(h)-(1-y).*log(1-h))/m;

或者不用sum()和点乘，用转置和矩阵乘法更快

y = [1 0 0 1]';
h = [0.8 0.2 0.1 0.9]';
m=4;
J = ((-y)'*log(h)-(1-y)'*log(1-h))/m;

这样得到的是二分类任务时的J

若为三分类任务，当为4个样本时，情况如下，y和h都变成了矩阵的形式。先说下矩阵的结构，行代表的是样本，列代表的是对应label的数值，例如y矩阵中，样本2的y=[0，0，1]，其实就是和上文所说的y维度发生了变了，原本样本2的label是3，所以对应的是[0，0，1]，上文的y的是列向量，这里是行向量代表一个样本，仅此而已，h矩阵的形式也同理

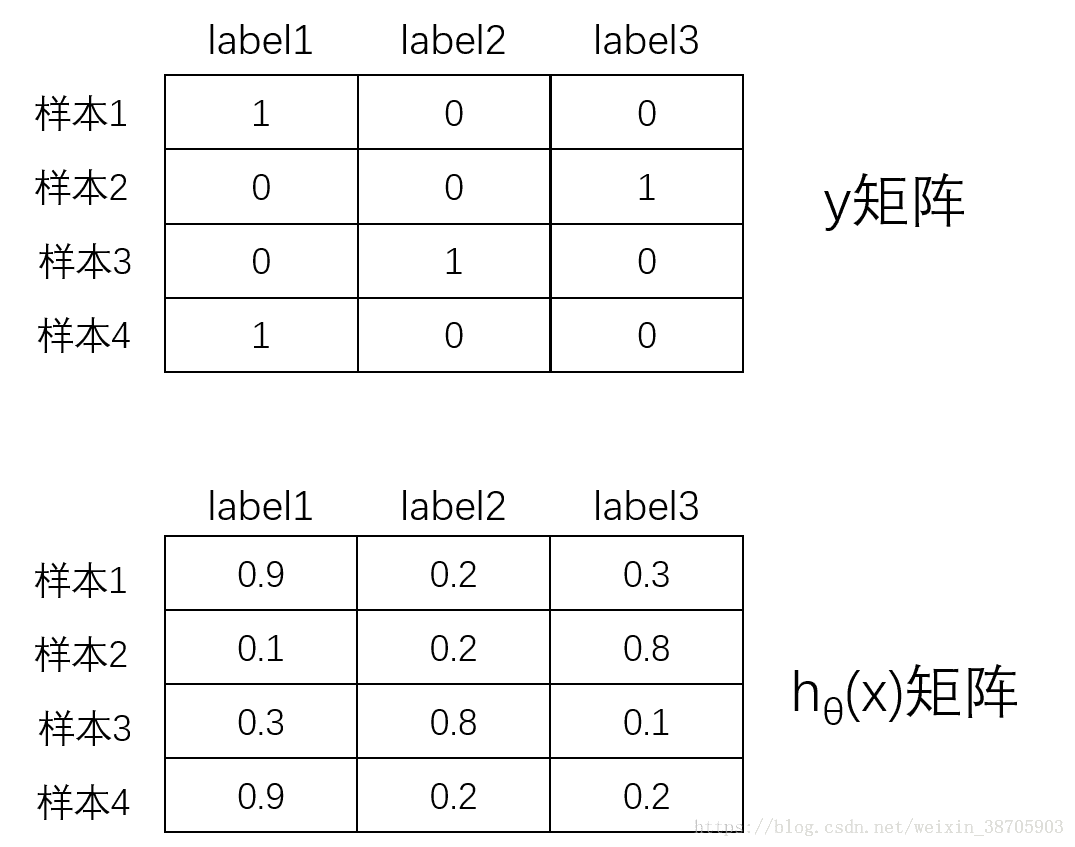
那么怎么在计算J的时候，是怎么研究y与h的关系的呢，其实三分类和二分类的原理都是一样的，不要因为数据的变成了矩阵就迷失了方向~

三分类我们也可以像二分类一样一个一个label慢慢看，首先我们先看三分类的label1（蓝色虚线框），可以把他当成是二分类的虚线框，也就是说在实际计算J的时候，

研究的是蓝色底色y与蓝色底色h的关系（对应样本1），黄色底色y与黄色底色h的关系（对应样本2），绿色底色y与绿色底色h的关系（对应样本3），橙色底色y与橙色底色h的关系（对应样本4）

那么label1是这样，label2和label3也是同理，J是表示预测值y与实际值h的关系的，所以只要样本之间数据不要对应错就好了

用代码计算J为

y = [1 0 0; 0 0 1; 0 1 0; 1 0 0];
h = [0.9 0.2 0.3; 0.1 0.2 0.8; 0.3 0.8 0.1; 0.9 0.2 0.2];
m = 4;
J = sum(sum((-y).*log(h)-(1-y).*log(1-h))/m);

仔细看你会发现J这里多了一个sum()，原因是因为二分类的时候，只有1列，所有只有求和一次，而在这里，不仅需要将所有样本的值进行求和，还要将所有label的J相加在一起，也就是多了个公式里的 ${\sum }_{k=1}^K$，求和时的J的变化过程如下

上面就是多分类时，J的计算过程

可能有朋友会问，代码采用转置+矩阵乘法不可以吗？请看下面

2. 矩阵乘法的坑

若用转置+矩阵乘法，代码为

y = [1 0 0; 0 0 1; 0 1 0; 1 0 0];
h = [0.9 0.2 0.3; 0.1 0.2 0.8; 0.3 0.8 0.1; 0.9 0.2 0.2];
m = 4;
J = sum(sum((-y)'*log(h)-(1-y)'*log(1-h))/m);

但是你会发现结果根本不对，原因是在矩阵乘法的时候，不仅会得到同一label下所有样本的J值，还有得到不同label下所有样本的J值

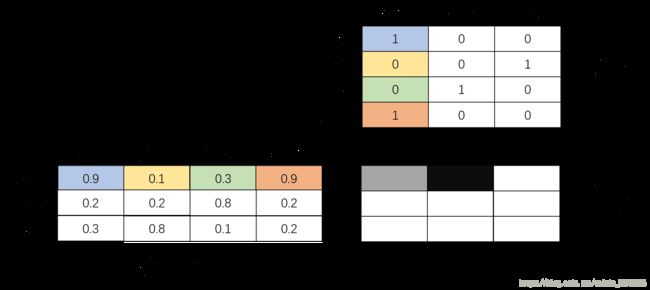
如图，结果矩阵中，灰色的格子为label1的所有样本的J直（即有颜色的格子对应相乘并求和），而黑色的格子是我们不需要的、因为矩阵乘法额外产生的数值

因此，如果想用矩阵乘法的话，我们只需要对角线的三个数值的就好
所以代码可以做如下更改，用diag()函数将对角线元素提取出来

y = [1 0 0; 0 0 1; 0 1 0; 1 0 0];
h = [0.9 0.2 0.3; 0.1 0.2 0.8; 0.3 0.8 0.1; 0.9 0.2 0.2];
m = 4;
J = sum(diag((-y)'*log(h)-(1-y)'*log(1-h))/m);

因为用的是矩阵乘法，所以只需要1个sum()即可
结果也为0.6184，问题解决~