机器学习----多项式回归详解
前言
我们在使用线性回归的时候有个局限性,就是他是假设数据背后是存在线性关系的,实际中这种情况还是比较少的。较多的还是非线性关系,多项式回归法正是解决数据之间非线性关系进行预测的机器学习算法,思路还是线性回归的原理。本质还是线性回归,只是增加了样本的特征。如下右图:将x、x^2当成两个特征。
在右图中 相当于在左边的基础上增加了一个特征x^2
上手实践
import numpy as np
import matplotlib.pyplot as plt
x=np.random.uniform(-3,3,size=100) #生成x特征 -3到3 100个
X=x.reshape(-1,1)#将x编程100行1列的矩阵
y=0.5*x**2+x+2+np.random.normal(0,1,size=100)#模拟的是标记y 对应的是x的二次函数
plt.scatter(x,y)#画出x,y散点图
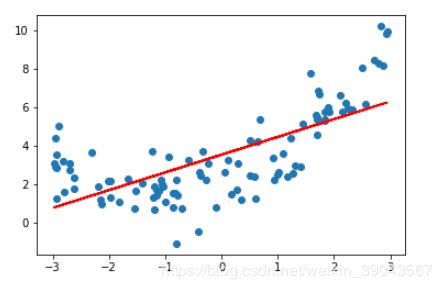
plt.show()这样的话如果我们按照之前的线性回归的方法去模拟的话:
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()#构造线性回归函数
lin_reg.fit(X,y)#根据X,y进行fit训练模型
y_pre=lin_reg.predict(X)#预测X对应的标记y
plt.scatter(X,y)
plt.plot(x,y_pre,color='r')#画图展示
plt.show()很显然这不是我们想要模拟的线,这种模拟也非常的不准确,如果能够用曲线进行模拟更好。
解决方法
y=ax^2+bx+c ,我们将x^2也看成一个特征,这样利用线性回归相当于二元线性回归进行使用。
lin_reg2 = LinearRegression()#另构造个函数
(X**2).shape#将X**2 相当于每个元素进行平方。universal
X2=np.hstack([X,X**2])#将X水平扩展一列 即X**2
X2.shape#查看后是100 x 2 的矩阵
lin_reg2.fit(X2,y)
y2_pre=lin_reg2.predict(X2)
plt.scatter(x,y)
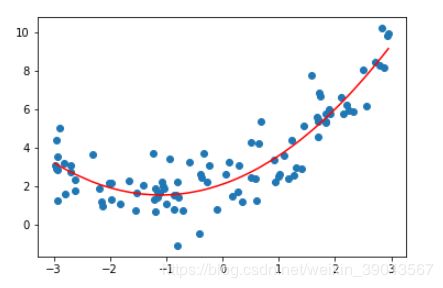
plt.plot(x,y2_pre,color='r') # 画出来的图这样,因为生成的x是没有顺序的 plt.scatter(x,y)
plt.plot(np.sort(x),y2_pre[np.argsort(x)],color='r') #将x进行排序,另外将x索引排序给y2_pre这样就完成了多项式回归,查看lin_reg2.intercept_截距为
2.1075838815460464查看系数lin_reg2.coef_
array([1.01781014, 0.46401187])正好符合我们模拟的函数 0.5x^2 +x ...
完全是LR的思路,只是增加了一列特征,这个特征是从原来特征的获取而来的 ,相当于升维,于PCA正好相反。
sklearn中怎么封装的多项式回归
封装了sklearn.preprocessing 的PolynomialFeatures
x=np.random.uniform(-3,3,size=100) #生成x特征 -3到3 100个
X=x.reshape(-1,1)#将x编程100行1列的矩阵
y=0.5*x**2+x+2+np.random.normal(0,1,size=100)#模拟的是标记y 对应的是x的二次函数
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree=2)#最多添加几次幂
#针对现有的特征X做相应的变形
poly.fit(X)
X2=poly.transform(X) #X2变成100行3列 第一列1 第二列是X 第三列X^2
lin_reg3=LinearRegression()
lin_reg3.fit(X2,y)
y3_pre=lin_reg3.predict(X2)
plt.scatter(x,y)
plt.plot(np.sort(x),y3_pre[np.argsort(x)],color='r')
lin_reg3.coef_#第一列为0是对X2中第一列1拟合的结果
lin_reg3.intercept_关于PolynomialFeatures
PolynomialFeatures是如何生成特征的 ,我们来观察一下,
X=np.arange(1,11).reshape(-1,2)#构造一个5行2列 作为5个样本 2个特征
poly=PolynomialFeatures(degree=2) #设置最高2次幂
poly.fit(X)
X2=poly.transform(X)
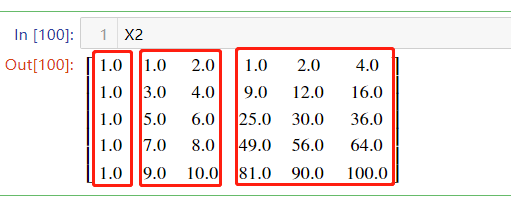
X2.shape#显示5行6列进行打印X2
观察X2我们发现 总共产生了6列,第一列全是1 相当于x^0,第2,3列就是原来的X^1,第4,5,6分别对应X中第一列的平方,X中1,2列的乘积,X中第2列的平方。
那我们在试试让degree=3 ,发现出现了更对的列!!
总结,如果有两个特征 x1 ,x2的话,当dgree=i的时候,会生成所有<=i的项,样本的特征数将指数级的上升。
Pipeline
问题? 如果dgree非常大的话 ,样本生成的特征就会很大 2^1和2^100差的很大的,我们再用线性回去的时候梯度下降法搜索相应结果,由于数据的分布很不均导致搜索过程很慢,此时用数据归一化解决。
Pipeline = 多项式特征+数据归一化+线性回归 将这三步合在一起,方便使用。
实现如下:
x=np.random.uniform(-3,3,size=100) #生成x特征 -3到3 100个
X=x.reshape(-1,1)#将x编程100行1列的矩阵
#我们选取的y是 4次幂的多项式 用来对比预测的结果 系数是否接近
y=x**4+2*x**3+0.5*x**2+x+2+np.random.normal(0,3,size=100)#模拟的是标记y 后面加了0-3噪音
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler#数据归一化
from sklearn.linear_model import LinearRegression #线性回归
poly_reg=Pipeline([#构建Pipeline
("poly",PolynomialFeatures(degree=3)),#构建PolynomialFeatures 进行多项式特征
("std_scaler",StandardScaler()),#构建归一化StandardScaler 进行数值的归一化
("lin_reg",LinearRegression())#构建线性回归LinearRegression 进行预测
])
#使用构建的Pipeline 自动的使用poly、std_scaler、lin_reg,其实sklearn没提供相应的多项式包
#时使用Pipeline进行预测的
poly_reg.fit(X,y)#Pipeline很智能的自动调用以上三步骤,是不是很爽?
y_pre =poly_reg.predict(X)#对进行多项式特征处理,数据归一化处理过的X进行预测
plt.scatter(x,y)
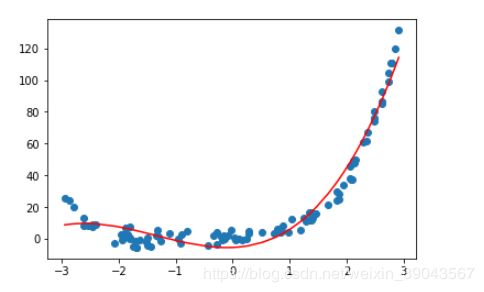
plt.plot(np.sort(x),y_pre[np.argsort(x)],color='r')
plt.show()
嘻嘻 这样就很号的拟合了4次的多项式哦~ ~