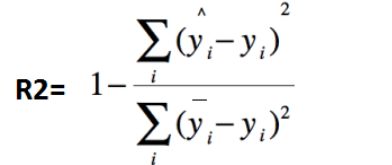回归评价指标：MSE、RMSE、MAE、MAPE、R2公式理解及代码实现

目录

预先假设：

平均绝对误差（MAE）

均方误差（MSE）均方根误差（RMSE） 

MAE：平均绝对误差；MAPE：平均绝对百分比误差

R2（R-Square）决定系数

通过sklearn库实现5种评价指标

预先假设：

平均绝对误差（MAE）

平均绝对误差（Mean Absolute Error）

范围[0,+∞)，当预测值与真实值完全吻合时等于0，即完美模型；误差越大，该值越大。MAE 的值越小，说明预测模型拥有更好的精确度。

import numpy as np
 
def mae_value(y_true, y_pred):
    """
    参数:
    y_true -- 测试集目标真实值
    y_pred -- 测试集目标预测值
    
    返回:
    mae -- MAE 评价指标
    """
    n = len(y_true)
    mae = sum(np.abs(y_true - y_pred))/n
    return mae

均方误差（MSE）均方根误差（RMSE） 

MASE它表示误差的平方的期望值。其实就是MSE加了个根号，这样数量级上比较直观，比如RMSE=10，可以认为回归效果相比真实值平均相差10。

import numpy as np
 
def mse_value(y_true, y_pred):
    """
    参数:
    y_true -- 测试集目标真实值
    y_pred -- 测试集目标预测值
    
    返回:
    mse -- MSE 评价指标
    """
    
    n = len(y_true)
    mse = sum(np.square(y_true - y_pred))/n
    return mse

MAE：平均绝对误差；MAPE：平均绝对百分比误差

平均绝对误差（Mean Absolute Error）；平均绝对百分比误差（Mean Absolute Percentage Error）

MAE:

范围[0,+∞)，当预测值与真实值完全吻合时等于0，即完美模型；误差越大，该值越大。

MAPE:

范围[0,+∞)，MAPE 为0%表示完美模型，MAPE 大于 100 %则表示劣质模型。MAPE 的值越小，说明预测模型拥有更好的精确度.

import numpy as np
 
def mape(y_true, y_pred):
    """
    参数:
    y_true -- 测试集目标真实值
    y_pred -- 测试集目标预测值
    
    返回:
    mape -- MAPE 评价指标
    """
    
    n = len(y_true)
    mape = sum(np.abs((y_true - y_pred)/y_true))/n*100
    return mape

R2（R-Square）决定系数

其中，分子部分表示真实值与预测值的平方差之和，类似于均方差 MSE；分母部分表示真实值与均值的平方差之和，类似于方差 Var。

根据 R-Squared 的取值，来判断模型的好坏，其取值范围为[0,1]：

如果结果是 0，说明模型拟合效果很差；

如果结果是 1，说明模型无错误。

一般来说，R-Squared 越大，表示模型拟合效果越好。

通过sklearn库实现5种评价指标

import numpy as np
from sklearn import metrics
from sklearn.metrics import r2_score#R square


# MAPE和SMAPE需要自己实现
def mape(y_true, y_pred):
    return np.mean(np.abs((y_pred - y_true) / y_true)) * 100

def smape(y_true, y_pred):
    return 2.0 * np.mean(np.abs(y_pred - y_true) / (np.abs(y_pred) + np.abs(y_true))) * 100

y_true = np.array([1.0, 5.0, 4.0, 3.0, 2.0, 5.0, -3.0])
y_pred = np.array([1.0, 4.5, 3.5, 5.0, 8.0, 4.5, 1.0])

# MSE
print(metrics.mean_squared_error(y_true, y_pred)) # 8.107142857142858
# RMSE
print(np.sqrt(metrics.mean_squared_error(y_true, y_pred))) # 2.847304489713536
# MAE
print(metrics.mean_absolute_error(y_true, y_pred)) # 1.9285714285714286
# MAPE
print(mape(y_true, y_pred)) # 76.07142857142858，即76%
# SMAPE
print(smape(y_true, y_pred)) # 57.76942355889724，即58%
print(r2_score(y_true,y_predict)