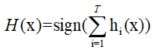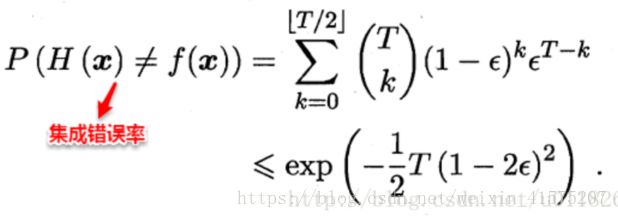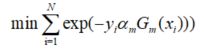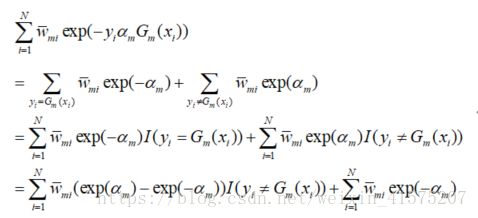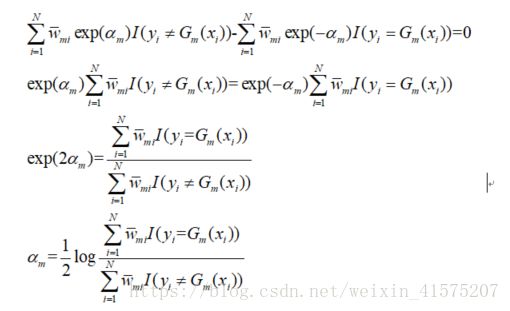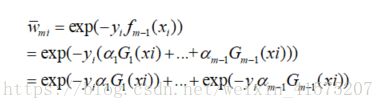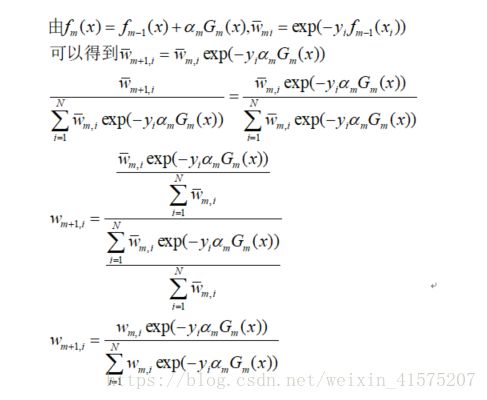机器学习-集成学习之AdaBoosting

第一次写博客,在机器学习的过程中CSDN上的博客帮助了我很多,在这里我也想分享下我对其中一些问题的看法。更重要的是想着在这里可以记录下点自己学习的过程,回过头来说不定也是美好的回忆

---

集成学习(ensemble learning)

集成学习指的,通过构建并结合多个学习器拉来完成学习任务.

个体与集成

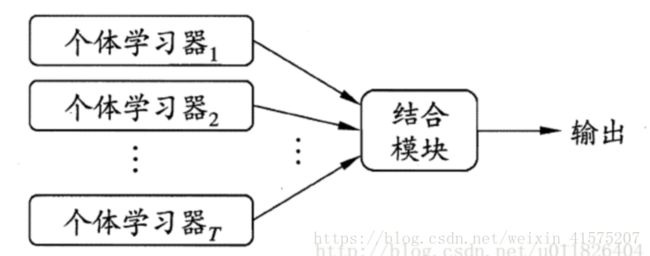
集成学习的一般结构为：先产生一组个体学习器，再用某种策略将它们结合在一起。

上图中,若个体学习器若个体学习器都属于同一类别，例如都是决策树或都是神经网络，则称该集成为同质的;其中学习器称为基学习器,对应的学习算法为基学习算法.

若个体学习器包含多种类型的学习算法，例如既有决策树又有神经网络，则称该集成为异质的。其中学习器称为组件学习器或者个体学习器.

我们已知集成学习器泛化性能总是比单个学习器都要好，虽说团结力量大但也有木桶短板理论调皮捣蛋，那如何做到呢？这就引出了集成学习的两个重要概念：准确性和多样性。

准确性指的是个体学习器不能太差，要有一定的准确度.

多样性则是个体学习器之间的输出要具有差异性.

通过下面的这三个例子可以很容易看出这一点，准确度较高，差异度也较高，可以较好地提升集成性能。

在二分类问题中，且错误率相等为 ε

若结合了T个基分类器,若其中有半数的基分类器正确,则集成分类正确:

假设基分类器错误率相互独立,则由于Hoeffding不等式可知,集成的错误率为:

---

 

集成器错误率随着基分类器的个数的增加呈指数下降，但前提是基分类器之间相互独立，在实际情形中显然是不可能的，假设训练有A和B两个分类器，对于某个测试样本，显然满足：P（A=1 | B=1）> P（A=1），因为A和B为了解决相同的问题而训练，因此在预测新样本时存在着很大的联系。因此，个体学习器的“准确性”和“差异性”本身就是一对矛盾的变量，准确性高意味着牺牲多样性，所以产生“好而不同”的个体学习器正是集成学习研究的核心。现阶段有三种主流的集成学习方法：Boosting、Bagging以及随机森林.

Boosting:

Boostiong是一族可以将弱学习器提升为强学习器的算法.

基本思想:先从初始训练集训练一个基础学习器,再根据基学习器的表现对训练样本的权重进行调整,然后基于调整后的样本进行训练下一个学习器如此重复得到T个学习器,最终将这T个学习器进行加权结合.

Boosting族中国最有代表性的是AdaBoosting.

AadBoosting:

输入:训练数据集T＝{(x1，y1),(x2，y2),…,(xN,yN)}，其中xi∊x⊆Rn，yi∊＝{-1,+1}；弱学习算法；

输出：最终分类器G(x)。

我们的目标是极小化分类错误:

鉴于AdaBoost采用加法模型:

选择指数函数作为损失函数:L(y,f(x))=exp(-yf(x))

PS:看了这么久其实我对这里选择指数函数作为损失函数还是有点一知半解,可能累加作为指数的幂可以转化为累乘,比较方便吧.

这样我们的目标就转化为极小化损失函数:上式中f(x)取决于,以为这我们希望找到极小值时候的

我们只需要保证

有最小值,且只要保证累加中每个部分均有最小值即可.

分两步走,先求G(x),在>0的情况下,最小的G(x)由下式得到：

 

可以理解为在权重影响下有最小分类错误率的G(x).

其后考虑

排除了G(x)的干扰,因为e的指数函数构成的上式显然不会存在最大值,现在对其求导使其为0,则会得到其最小值.

对上式求导

这里我们看到和两个因素有关:分类的正误和一个随着f(x)变化的参数,这里变量太多了.我们希望可以转化为与一个因素有关:

---

对做以下转化

对w做以下转化

我们可以发现有如下关系:

在把其余分类错误率联系起来,希望把变量固定为一个

---

最后我们得到:

可见只和分类错误率有关,所以我们只要保持每次基学习器的分类错误率一直为最小即可.

如何更新权值分布:                                                                                                                                                                              

  这也解释了规范化因子的由来.

 最后对基学习器进行线性组合就可以得到最终学习器. 

   参考:  

周志华机器学习

https://blog.csdn.net/u011826404/article/details/70172971

李航 统计学习方法